X-Bar-S图和X-Bar-R图是统计质量控制中常用的两种控制图,用于监测过程的稳定性和一致性。它们的主要区别在于如何计算和呈现数据的变化以及所关注的问题类型。
-
X-Bar-S图(平均值与标准偏差图):
- X-Bar代表样本均值,S代表样本标准偏差。
- X-Bar-S图用于监测过程的平均值和变异性。
- 过程中的每个样本都会测量,并计算出该样本的平均值(X-Bar)和标准偏差(S)。
- 控制图上通常有两条中心线:一条代表平均值,另一条代表标准偏差。
- X-Bar-S图适用于对过程均值和过程标准偏差都有关注的情况,例如,需要确保产品的尺寸和质量稳定。
-
X-Bar-R图(平均值与范围图):
- X-Bar代表样本均值,R代表样本范围。
- X-Bar-R图主要用于监测过程的平均值和范围,而不是标准偏差。
- 对每个样本进行测量,并计算出该样本的平均值(X-Bar)和范围(R,即最大值与最小值之差)。
- 控制图上通常有两条中心线:一条代表平均值,另一条代表范围。
- X-Bar-R图适用于关注过程的平均值,但不太关注过程的标准偏差的情况,例如,需要确保生产过程的平均值在目标值附近。
总之,X-Bar-S图和X-Bar-R图都用于监测过程的稳定性,但它们关注的参数不同。X-Bar-S图同时关注平均值和标准偏差,而X-Bar-R图关注平均值和样本范围。选择使用哪种图表取决于你对过程的关注点和需要监测的参数。
------------------------
下面是X-Bar-S图和X-Bar-R图的各自控制限计算公式:
X-Bar-S图的控制限计算公式:
-
上控制限(UCL)和下控制限(LCL)用于X-Bar图(平均值图):
- UCL(X-Bar) = X-Double Bar + A3 * S-Bar
- LCL(X-Bar) = X-Double Bar - A3 * S-Bar
其中,X-Double Bar是所有样本平均值的平均值,A3是与样本容量相关的常数,S-Bar是所有样本标准偏差的平均值。
-
上控制限(UCL)和下控制限(LCL)用于S图(标准偏差图):
- UCL(S) = B4 * S-Bar
- LCL(S) = B3 * S-Bar
其中,B3和B4是与样本容量相关的常数,S-Bar是所有样本标准偏差的平均值。
X-Bar-R图的控制限计算公式:
-
上控制限(UCL)和下控制限(LCL)用于X-Bar图(平均值图):
- UCL(X-Bar) = X-Double Bar + A2 * R-Bar
- LCL(X-Bar) = X-Double Bar - A2 * R-Bar
其中,X-Double Bar是所有样本平均值的平均值,A2是与样本容量相关的常数,R-Bar是所有样本范围的平均值。
-
上控制限(UCL)和下控制限(LCL)用于R图(范围图):
- UCL(R) = D4 * R-Bar
- LCL(R) = D3 * R-Bar
其中,D3和D4是与样本容量相关的常数,R-Bar是所有样本范围的平均值。
这些常数(如A2、B3、B4、D3和D4)取决于样本容量和所选的控制图类型,通常可以在统计参考表中找到相应的值。控制限的目标是帮助检测过程中任何异常或变化,以便及时采取纠正措施来维持过程的稳定性。
--------------
两种X-Bar控制图(X-Bar-S图和X-Bar-R图)的平均值图计算方法不同,是因为它们关注的参数和控制图的目的不同,这导致了不同的控制限计算方法。
-
X-Bar-S图的平均值图(X-Bar图):
- X-Bar-S图用于监测过程的平均值和标准偏差。它关注的是过程的整体平均水平以及过程中的变异性。
- 平均值图的上控制限(UCL)和下控制限(LCL)计算方法包括平均值(X-Bar)和标准偏差(S-Bar)的组合,因为在X-Bar-S图中,两者都是关注的参数。
- 控制限的目的是确保过程的平均值和标准偏差保持在可接受的范围内。
-
X-Bar-R图的平均值图(X-Bar图):
- X-Bar-R图用于监测过程的平均值和范围(即最大值与最小值之差)。它关注的是过程的平均水平和过程的范围变化。
- 平均值图的上控制限(UCL)和下控制限(LCL)计算方法包括平均值(X-Bar)和范围(R-Bar)的组合,因为在X-Bar-R图中,这两个参数是关注的。
- 控制限的目的是确保过程的平均值和范围保持在可接受的范围内。
因此,不同的控制图类型具有不同的控制限计算方法,以反映它们关注的参数和过程监测的目的。选择使用哪种图表取决于你对过程的关注点,例如,是更关注标准偏差还是范围的变化。
----------
X-Bar-R 控制图是一种用于监测过程稳定性和一致性的质量控制工具。首先,我们需要计算每组数据的平均值和范围,然后绘制控制图,并计算CPK以及合格率。
-
计算每组数据的平均值和范围: 对于每组数据,计算平均值和范围。范围(R)是每组数据中最大值与最小值的差异。
-
计算 X-Bar 控制图: a. 计算所有平均值的平均值(X-双点中心线)。 b. 绘制 X-Bar 控制图,将每组的平均值分布在图上。
-
计算 R 控制图: a. 计算所有范围值的平均值(R-双点中心线)。 b. 绘制 R 控制图,将每组的范围值分布在图上。
-
计算控制限: a. 计算 X-Bar 控制图的控制限,可以使用标准的控制图公式,通常为 X-Bar 的平均值加减 3 倍 R 的平均值。 b. 计算 R 控制图的控制限,通常为 R 的平均值乘以一个常数因子。
-
计算CPK(过程能力指数): CPK = min[(USL - X-双点中心线) / (3 * 标准差), (X-双点中心线 - LSL) / (3 * 标准差)] 其中,USL是产品规格上限,LSL是产品规格下限。
-
sigma 表示过程的标准差,它是通过控制图中的平均范围R 来估计的。
在控制图中,R 通常代表一组样本数据的范围,而 d2 是控制图常数,它是用于校正范围以估计标准差的。
sigma 被计算为:sigma = (平均范围R) / d2 -
计算产品规格上下限间的合格率: 使用正态分布表或统计软件,根据CPK值和规格上下限,计算出合格率。
这些步骤需要一些数据处理和图表绘制,最好使用统计软件或工具来执行。确保准确地计算平均值、范围、控制限、CPK,以及合格率。
----------
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import scipy.stats as stats
plt.rcParams['font.sans-serif'] = ['SimHei'] # 防止中文标签乱码
plt.rcParams['axes.unicode_minus'] = Falsedf = pd.read_excel('GuanZi1011.xlsx') #<class 'pandas.core.frame.DataFrame'>
# print(data)# print(df.columns)
# print(df.info)# 计算每组的平均值(X-Bar)
x_bar = df.mean(axis=0) # pandas Series # 计算每组的样本标准差(S)
s = df.std(axis=0, ddof=1)# # [10 rows x 10 columns] 10组,10个数据/组
# 固定的A2、B3、B4值
A3 = 0.975
B3 = 0.284
B4 = 1.716# 计算X-Bar控制图的控制限
X_Double_Bar = x_bar.mean()
S_Bar = s.mean()UCL_X_Bar = X_Double_Bar + A3 * S_Bar
LCL_X_Bar = X_Double_Bar - A3 * S_Barprint(f"UCL_X_Bar: {UCL_X_Bar}",f"LCL_X_Bar: {LCL_X_Bar}")# 计算S控制图的控制限
UCL_S = B4 * S_Bar
LCL_S = B3 * S_Bar# 创建X-Bar 控制图,添加上下控制限
plt.figure(figsize=(5.3, 6))
plt.subplot(2, 1, 1)
plt.plot(x_bar, marker='o')
plt.axhline(X_Double_Bar, color='r', linestyle='--', label='Overall Mean')
plt.axhline(UCL_X_Bar, color='g', linestyle='--', label='UCL')
plt.axhline(LCL_X_Bar, color='b', linestyle='--', label='LCL')
plt.title('X-Bar Control Chart')
# plt.xlabel('Sample Group')
plt.ylabel('X-Bar')
plt.legend()# 创建S 控制图,添加上下控制限
plt.subplot(2, 1, 2)
plt.plot(s, marker='o')
plt.axhline(S_Bar, color='r', linestyle='--', label='Overall Mean')
plt.axhline(UCL_S, color='g', linestyle='--', label='UCL')
plt.axhline(LCL_S, color='b', linestyle='--', label='LCL')
plt.title('S Control Chart')
# plt.xlabel('Sample Group')
plt.ylabel('S')
plt.legend()plt.tight_layout()
plt.show()# X-Bar-S图 控制限计算公式:
# UCL(X-Bar) = X-Double Bar + A3 * S-Bar
# LCL(X-Bar) = X-Double Bar - A3 * S-Bar
# UCL(S) = B4 * S-Bar
# LCL(S) = B3 * S-Bar# X-Bar-R图的控制限计算公式:
# UCL(X-Bar) = X-Double Bar + A2 * R-Bar
# LCL(X-Bar) = X-Double Bar - A2 * R-Bar
# UCL(R) = D4 * R-Bar
# LCL(R) = D3 * R-Barimport numpy as np
import matplotlib.pyplot as plt# 生成10组每组10个数据的示例数据(总共100个数据)
np.random.seed(0)
data = np.random.randn(10, 10)# 计算每组的平均值(X-Bar)
x_bar = np.mean(data, axis=1)# 计算每组的极差(R)
r = np.ptp(data, axis=1)# 固定的A2、D4、D3值
A2 = 0.308
D4 = 1.777
D3 = 0.223# 计算X-Bar控制图的控制限
X_Double_Bar = np.mean(x_bar)
R_Bar = np.mean(r)
UCL_X_Bar = X_Double_Bar + A2 * R_Bar
LCL_X_Bar = X_Double_Bar - A2 * R_Bar# 计算R控制图的控制限
UCL_R = D4 * R_Bar
LCL_R = D3 * R_Bar# 创建X-Bar 控制图,添加上下控制限
plt.figure(figsize=(12, 6))
plt.subplot(2, 1, 1)
plt.plot(x_bar, marker='o')
plt.axhline(X_Double_Bar, color='r', linestyle='--', label='Overall Mean')
plt.axhline(UCL_X_Bar, color='g', linestyle='--', label='UCL')
plt.axhline(LCL_X_Bar, color='b', linestyle='--', label='LCL')
plt.title('X-Bar Control Chart')
plt.xlabel('Sample Group')
plt.ylabel('X-Bar')
plt.legend()# 创建R 控制图,添加上下控制限
plt.subplot(2, 1, 2)
plt.plot(r, marker='o')
plt.axhline(R_Bar, color='r', linestyle='--', label='Overall Mean')
plt.axhline(UCL_R, color='g', linestyle='--', label='UCL')
plt.axhline(LCL_R, color='b', linestyle='--', label='LCL')
plt.title('R Control Chart')
plt.xlabel('Sample Group')
plt.ylabel('R')
plt.legend()plt.tight_layout()
plt.show()
绘制X-Bar-R图,监测过程,计算CPK过程能力指数
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
import pandas as pdplt.rcParams['font.sans-serif'] = ['SimHei'] # 防止中文标签乱码
plt.rcParams['axes.unicode_minus'] = False# 替换下面的数据为你的实际数据
data = pd.read_excel('GuanZi1011.xlsx')# 计算每组样本的平均值
x_bar = data.mean(axis=0) # Series# 计算每组样本的范围R
r = data.max(axis=0) - data.min(axis=0)x_bar_avg = np.mean(x_bar)
r_avg = np.mean(r)print(f'x_bar_avg: {x_bar_avg}')
print(f'r_avg: {r_avg}')# X-Bar-R图的控制系数 # [10 rows x 10 columns]
d2 = 3.078 # R控制图的常数,可以根据样本大小查表获取
A2 = 0.308 # X-Bar控制图的常数,可以根据样本大小查表获取
D4 = 1.777 # R控制图的常数,可以根据样本大小查表获取
D3 = 0.223 # R控制图的常数,可以根据样本大小查表获取USL = 5.1 # 规格上限
LSL = 4.9 # 规格下限# sigma 表示过程的标准差,它是通过控制图中的平均范围R 来估计的。
# 在控制图中,R 通常代表一组样本数据的范围,而 d2 是控制图常数,它是用于校正范围以估计标准差的。
# sigma 被计算为:sigma = (平均范围R) / d2
sigma = r_avg / d2# Z 分数(即标准分数,Z = (x - μ) / σ)根据数据点与一组点的平均值和标准偏差之间的关系来描述数据点
Zscore = min((USL - x_bar_avg) / sigma, (x_bar_avg - LSL) / sigma)# 计算CPK(过程能力指数):
# CPK = min[(USL - X-双点中心线) / (3 * 标准差), (X-双点中心线 - LSL) / (3 * 标准差)]
# 其中,USL是产品规格上限,LSL是产品规格下限。
cpk = min((USL - x_bar_avg) / (3 * sigma), (x_bar_avg - LSL) / (3 * sigma))
# 计算合格率
z_upper = (USL - x_bar_avg) / (sigma)
z_lower = (LSL - x_bar_avg) / (sigma)
cpk_area = norm.cdf(z_upper,0,1) - norm.cdf(z_lower,0,1)
cp= (USL-LSL) / (6* sigma) # 规格范围相对于过程的变异性有多宽
ppm = (1 - cpk_area) * 1000000 ## 换算成每百万机会的不合格品数print(f'sigma: {sigma}')
print(f'Zscore: {Zscore}')
print(f'CPK: {cpk}')
print(f"cpk_area:{cpk_area}")
print("CP:", cp)
print(f'PPM: {ppm}')# X-Bar-R图的控制限计算公式:
# UCL(X-Bar) = X-Double Bar + A2 * R-Bar
# LCL(X-Bar) = X-Double Bar - A2 * R-Bar
# UCL(R) = D4 * R-Bar
# LCL(R) = D3 * R-Barx_bar_UCL = x_bar_avg + A2 * r_avg
x_bar_LCL = x_bar_avg - A2 * r_avgr_UCL = D4 * r_avg
r_LCL = D3 * r_avg# 绘制X-Bar控制图
plt.figure(figsize=(7, 6))
plt.subplot(2, 1, 1)
plt.plot(x_bar, marker='o')
plt.axhline(x_bar_avg, color='r', linestyle='--', label='X-Bar Center Line')
plt.axhline(x_bar_UCL, color='g', linestyle='--', label='X-Bar UCL')
plt.axhline(x_bar_LCL, color='g', linestyle='--', label='X-Bar LCL')
plt.title('X-Bar Control Chart')
plt.legend()
plt.grid()# 绘制R控制图
plt.subplot(2, 1, 2)
plt.plot(r, marker='o')
plt.axhline(r_avg, color='r', linestyle='--', label='R Center Line')
plt.axhline(r_UCL, color='g', linestyle='--', label='R UCL')
plt.axhline(r_LCL, color='g', linestyle='--', label='R LCL')
plt.title('R Control Chart')
plt.legend()
plt.grid()
plt.show()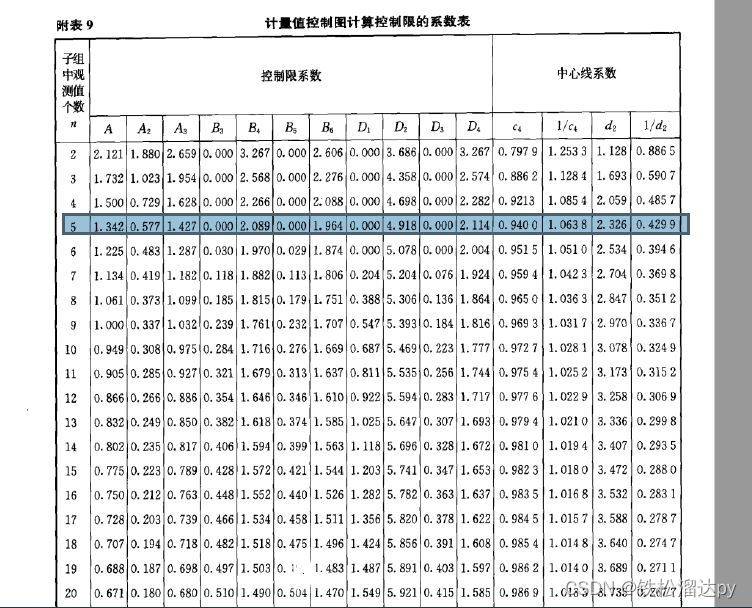
# X-Bar-S图 控制限计算公式:
# UCL(X-Bar) = X-Double Bar + A3 * S-Bar
# LCL(X-Bar) = X-Double Bar - A3 * S-Bar
# UCL(S) = B4 * S-Bar
# LCL(S) = B3 * S-Bar
# X-Bar-R图的控制限计算公式:
# UCL(X-Bar) = X-Double Bar + A2 * R-Bar
# LCL(X-Bar) = X-Double Bar - A2 * R-Bar
# UCL(R) = D4 * R-Bar
# LCL(R) = D3 * R-Bar