很高兴在雪易的CSDN遇见你 ,给你糖糖![]()
![]()
![]()
欢迎大家加入雪易社区-CSDN社区云
前言
本文分享VTK基础操作技术,记录vtk编程中常用的接口,变量等的创建及使用方法希望对各位小伙伴有所帮助!
感谢各位小伙伴的点赞+关注,小易会继续努力分享,一起进步!
你的点赞就是我的动力(^U^)ノ~YO
目录
前言
1. vtkDoubleArray参数的创建
2. 已知方向v1,v2,计算法向量n
3. 计算点到有限直线的距离
4. 计算vtkPolygon的法线
5. vtkPlaneCollection的声明和遍历
6. 遍历不同类型的Cell
7. 三角形条带生成三角形规则
8. 实体与Surface的区别
9. vtkPriorityQueue 优先队列
10. 计算polygon的面积
11. vtkPolyData->vtkActor & vtkActor->vtkPolyData变换过程
12. 打印Print信息
1. vtkDoubleArray参数的创建
//代码摘自vtkPolyPlane的ComputeNormal函数中
const vtkIdType = 5;
vtkDoubleArray* Normals = vtkDoubleArray::New();
Normals->SetNumberOfComponents(3);
Normals->Allocate(3 * nLines);
Normals->SetName("Normals");
Normals->SetNumberOfTuples(nLines);
2. 已知方向v1,v2,计算法向量n
vtkMath::Cross(v1, v2, n);
vtkMath::Normalize(n);3. 计算点到有限直线的距离
// Compute distance to finite line. Returns parametric coordinate t
// and point location on line.
double vtkLine::DistanceToLine(const double x[3], const double p1[3], const double p2[3], double& t, double closestPoint[3])
{const double* closest = nullptr;//// Determine appropriate vectors// 计算P21向量double p21[3] = { p2[0] - p1[0], p2[1] - p1[1], p2[2] - p1[2] };//// Get parametric location// 计算x点到P21为法向量的平面的距离double num = p21[0] * (x[0] - p1[0]) + p21[1] * (x[1] - p1[1]) + p21[2] * (x[2] - p1[2]);if (num == 0.0){//若距离为0表示,x与p1点重合t = 0;closest = p1;}else{//计算p21点到p21为法向量的平面的距离double denom = vtkMath::Dot(p21, p21);// trying to avoid an expensive fabsdouble tolerance = VTK_TOL * num;//计算误差if (tolerance < 0.0){tolerance = -tolerance;}if (denom < tolerance) // numerically bad!{//若p21点到平面的距离小于误差,若num>0,表示最近点为p2;反之为p1if (num > 0){closest = p2;t = VTK_DOUBLE_MAX;}else{closest = p1;t = VTK_DOUBLE_MIN;}}//// If parametric coordinate is within 0<=p<=1, then the point is closest to// the line. Otherwise, it's closest to a point at the end of the line.//else if ((t = num / denom) < 0.0){//若x点与p21点的方向不一致,则最近点为p1closest = p1;}else if (t > 1.0){closest = p2;}else{closest = p21;p21[0] = p1[0] + t * p21[0];p21[1] = p1[1] + t * p21[1];p21[2] = p1[2] + t * p21[2];}}//计算x到直线Line12的最近点。if (closestPoint){closestPoint[0] = closest[0];closestPoint[1] = closest[1];closestPoint[2] = closest[2];}//返回x与最近点的距离的平方return vtkMath::Distance2BetweenPoints(closest, x);
}4. 计算vtkPolygon的法线
void vtkPolygon::ComputeNormal(vtkPoints* p, int numPts, const vtkIdType* pts, double* n)
{int i;double v[3][3], *v0 = v[0], *v1 = v[1], *v2 = v[2], *tmp;double ax, ay, az, bx, by, bz;//// Check for special triangle case. Saves extra work.//n[0] = n[1] = n[2] = 0.0;if (numPts < 3){return;}if (numPts == 3){if (pts){p->GetPoint(pts[0], v0);p->GetPoint(pts[1], v1);p->GetPoint(pts[2], v2);}else{p->GetPoint(0, v0);p->GetPoint(1, v1);p->GetPoint(2, v2);}vtkTriangle::ComputeNormal(v0, v1, v2, n);return;}// Because polygon may be concave, need to accumulate cross products to// determine true normal.//// set things up for loopif (pts){p->GetPoint(pts[0], v1);p->GetPoint(pts[1], v2);}else{p->GetPoint(0, v1);p->GetPoint(1, v2);}for (i = 0; i < numPts; i++){tmp = v0;v0 = v1;v1 = v2;v2 = tmp;if (pts){p->GetPoint(pts[(i + 2) % numPts], v2);}else{p->GetPoint((i + 2) % numPts, v2);}// order is important!!! to maintain consistency with polygon vertex orderax = v2[0] - v1[0];ay = v2[1] - v1[1];az = v2[2] - v1[2];bx = v0[0] - v1[0];by = v0[1] - v1[1];bz = v0[2] - v1[2];n[0] += (ay * bz - az * by);n[1] += (az * bx - ax * bz);n[2] += (ax * by - ay * bx);}vtkMath::Normalize(n);
}5. vtkPlaneCollection的声明和遍历
vtkNew<vtkPlaneCollection> planes;
vtkNew<vtkPlane> plane;
plane->SetOrigin(origin);
plane->SetNormal(normal);
planes->AddItem(plane);vtkCollectionSimpleIterator iter;
int numPlanes = 0;
if(planes)
{planes->InitTraversal(iter);numPlanes = planes->GetNumberOfItems();vtkPlane* plane = nullptr;for (int planeId = 0; planes && (plane = planes->GetNextPlane(iter)); planeId++){//plane 操作}
}6. 遍历不同类型的Cell
vtkPolyData* inputDS = ...
vtkCellArray* inputPolys = inputDS->GetPolys();const vtkIdType* pts = nullptr;
vtkIdType cellId, npts;
for(cellId = 0, inputPolys->InitTraversal(); inputPolys->GetNextCell(npts, pts); cellId++)
{...
}vtkCellArray *inVerts = input->GetVerts();
for (inVerts = input->GetVerts(), inVerts->InitTraversal(); inVerts->GetNextCell(npts, pts);)
{for (j = 0; j < npts; j++){Verts[pts[j]].type = VTK_FIXED_VERTEX;}
}// 同理对于Line7. 三角形条带生成三角形规则
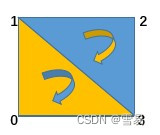
vtkCellArray* strips = vtkCellArray::New();
strips->InsertNextCell(4);
strips->InsertCellPoint(0);
strips->InsertCellPoint(1);
strips->InsertCellPoint(3);
strips->InsertCellPoint(2);生成的三角形为(0,1,3)和(3,1,2)。
8. 实体与Surface的区别
实体的所有Triangle的方向均指向内部。
9. vtkPriorityQueue 优先队列
vtkPriorityQueue* leftmostPoints = vtkPriorityQueue::New();
leftmostPoints->Allocate(8);
leftmostPoints->Insert(-10, 0);
leftmostPoints->Insert(10, 1);
leftmostPoints->Insert(-3, 2);
leftmostPoints->Insert(0, 3);
leftmostPoints->Insert(2, 4);
leftmostPoints->Insert(5, 5);
leftmostPoints->Insert(-80, 6);
leftmostPoints->Insert(30, 7);
while (leftmostPoints->GetNumberOfItems())
{vtkIdType currentPointID = leftmostPoints->Pop();
//currentPointID分别为6,0,2,3,4,5,1,7
}
10. 计算polygon的面积
vtkSphere::ComputeBoundingSphere(static_cast<vtkDoubleArray*>(polygon->Points->GetData())->GetPointer(0),polygon->PointIds->GetNumberOfIds(), sphere, hints);
//if (sphere[3] <= this->HoleSize)
//sphere[3]为polygon的面积11. vtkPolyData->vtkActor & vtkActor->vtkPolyData变换过程
vtkPolyData* pd = ...;
vtkPolyDataMapper* mapper = vtkPolyDataMapper::New();
mapper->setInputData(pd);
vtkActor* actor = vtkActor::New();
actor->setMapper(mapper);//vtkPolyData改变驱动vtkActor改变
pd->Modified(); //关联的Actor会自动更新//vtkActor改变(发生移动或旋转等),并不会驱动关联的PolyData数据进行改变
//1. 获取vtkActor变换矩阵
//2. 将变换矩阵作用于关联的PolyData对象即可。12. 打印Print信息
vtkPolyData* pd;
pd->Print(std::cout)感谢各位小伙伴的点赞+关注,小易会继续努力分享,一起进步!
你的赞赏是我的最最最最大的动力(^U^)ノ~YO