B树
前言
首先,为什么要总结B树、B+树的知识呢?最近在学习数据库索引调优相关知识,数据库系统普遍采用B-/+Tree作为索引结构(例如mysql的InnoDB引擎使用的B+树),理解不透彻B树,则无法理解数据库的索引机制;接下来将用最简洁直白的内容来了解B树、B+树的数据结构
另外,B-树,即为B树。因为B树的原英文名称为B-tree,而国内很多人喜欢把B-tree译作B-树,其实,这是个非常不好的直译,很容易让人产生误解。如人们可能会以为B-树是一种树,而B树又是一种树。而事实上是,B-tree就是指的B树,目前理解B的意思为平衡
B树的出现是为了弥合不同的存储级别之间的访问速度上的巨大差异,实现高效的 I/O。平衡二叉树的查找效率是非常高的,并可以通过降低树的深度来提高查找的效率。但是当数据量非常大,树的存储的元素数量是有限的,这样会导致二叉查找树结构由于树的深度过大而造成磁盘I/O读写过于频繁,进而导致查询效率低下。另外数据量过大会导致内存空间不够容纳平衡二叉树所有结点的情况。B树是解决这个问题的很好的结构
概念
首先,B树不要和二叉树混淆,在计算机科学中,B树是一种自平衡树数据结构,它维护有序数据并允许以对数时间进行搜索,顺序访问,插入和删除。B树是二叉搜索树的一般化,因为节点可以有两个以上的子节点。[1]与其他自平衡二进制搜索树不同,B树非常适合读取和写入相对较大的数据块(如光盘)的存储系统。它通常用于数据库和文件系统。
定义
B树是一种平衡的多分树,通常我们说m阶的B树,它必须满足如下条件:
- 每个节点最多只有m个子节点。
- 每个非叶子节点(除了根)具有至少⌈ m/2⌉子节点。
- 如果根不是叶节点,则根至少有两个子节点。
- 具有k个子节点的非叶节点包含k -1个键。
- 所有叶子都出现在同一水平,没有任何信息(高度一致)。
第一次看到这个定义的时候,在想什么鬼?。。。。什么是阶?子节点、飞叶子点、根???啥意思!少年别慌。。。
什么是B树的阶 ?
B树中一个节点的子节点数目的最大值,用m表示,假如最大值为10,则为10阶,如图

所有节点中,节点【13,16,19】拥有的子节点数目最多,四个子节点(灰色节点),所以可以定义上面的图片为4阶B树,现在懂什么是阶了吧
什么是根节点 ?
节点【10】即为根节点,特征:根节点拥有的子节点数量的上限和内部节点相同,如果根节点不是树中唯一节点的话,至少有俩个子节点(不然就变成单支了)。在m阶B树中(根节点非树中唯一节点),那么有关系式2<= M <=m,M为子节点数量;包含的元素数量 1<= K <=m-1,K为元素数量。
什么是内部节点 ?
节点【13,16,19】、节点【3,6】都为内部节点,特征:内部节点是除叶子节点和根节点之外的所有节点,拥有父节点和子节点。假定m阶B树的内部节点的子节点数量为M,则一定要符合(m/2)<= M <=m关系式,包含元素数量M-1;包含的元素数量 (m/2)-1<= K <=m-1,K为元素数量。m/2向上取整。
什么是叶子节点?
节点【1,2】、节点【11,12】等最后一层都为叶子节点,叶子节点对元素的数量有相同的限制,但是没有子节点,也没有指向子节点的指针。特征:在m阶B树中叶子节点的元素符合(m/2)-1<= K <=m-1。
好了,概念已经清楚,不用着急背公式, 接着往下看
插入
针对m阶高度h的B树,插入一个元素时,首先在B树中是否存在,如果不存在,即在叶子结点处结束,然后在叶子结点中插入该新的元素。
- 若该节点元素个数小于m-1,直接插入;
- 若该节点元素个数等于m-1,引起节点分裂;以该节点中间元素为分界,取中间元素(偶数个数,中间两个随机选取)插入到父节点中;
- 重复上面动作,直到所有节点符合B树的规则;最坏的情况一直分裂到根节点,生成新的根节点,高度增加1;
上面三段话为插入动作的核心,接下来以5阶B树为例,详细讲解插入的动作;
5阶B树关键点:
- 2<=根节点子节点个数<=5
- 3<=内节点子节点个数<=5
- 1<=根节点元素个数<=4
- 2<=非根节点元素个数<=4
插入8

图(1)插入元素【8】后变为图(2),此时根节点元素个数为5,不符合 1<=根节点元素个数<=4,进行分裂(真实情况是先分裂,然后插入元素,这里是为了直观而先插入元素,下面的操作都一样,不再赘述),取节点中间元素【7】,加入到父节点,左右分裂为2个节点,如图(3)

接着插入元素【5】,【11】,【17】时,不需要任何分裂操作,如图(4)
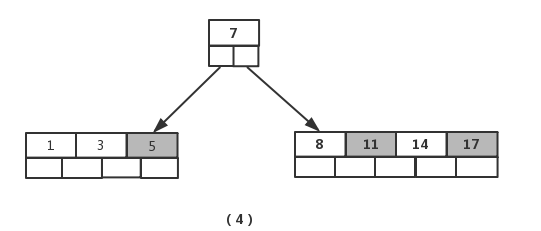
插入元素【13】
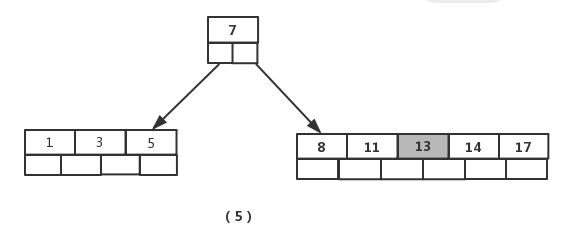
节点元素超出最大数量,进行分裂,提取中间元素【13】,插入到父节点当中,如图(6)
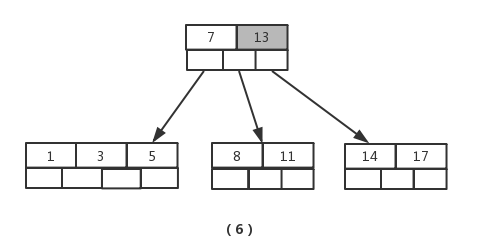
接着插入元素【6】,【12】,【20】,【23】时,不需要任何分裂操作,如图(7)
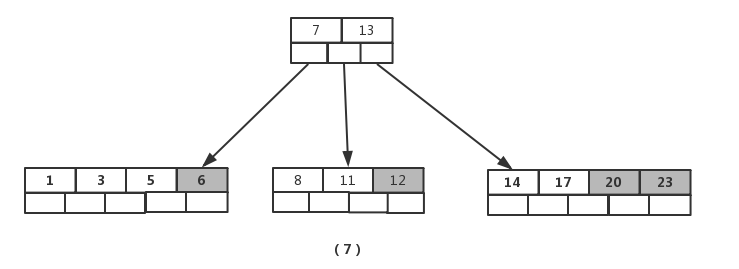
插入【26】时,最右的叶子结点空间满了,需要进行分裂操作,中间元素【20】上移到父节点中,注意通过上移中间元素,树最终还是保持平衡,分裂结果的结点存在2个关键字元素。
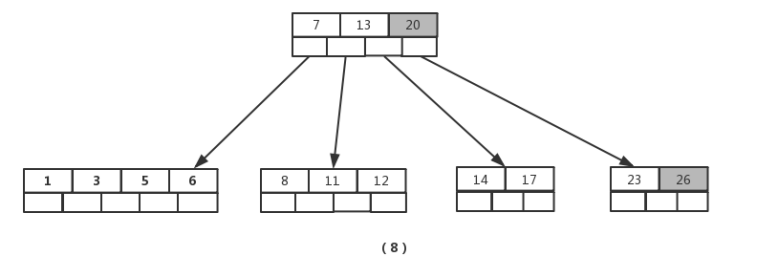
插入【4】时,导致最左边的叶子结点被分裂,【4】恰好也是中间元素,上移到父节点中,然后元素【16】,【18】,【24】,【25】陆续插入不需要任何分裂操作
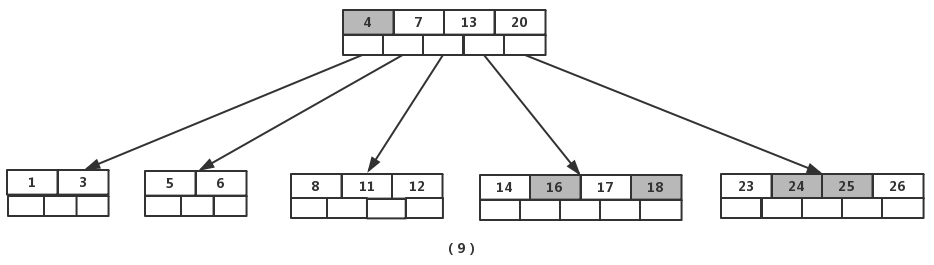
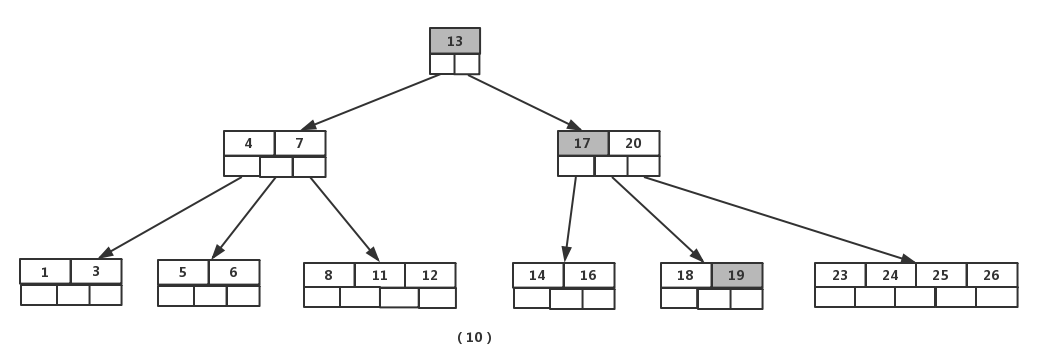
最后,当插入【19】时,含有【14】,【16】,【17】,【18】的结点需要分裂,把中间元素【17】上移到父节点中,但是情况来了,父节点中空间已经满了,所以也要进行分裂,将父节点中的中间元素【13】上移到新形成的根结点中,这样具体插入操作的完成。
删除
首先查找B树中需删除的元素,如果该元素在B树中存在,则将该元素在其结点中进行删除;删除该元素后,首先判断该元素是否有左右孩子结点,如果有,则上移孩子结点中的某相近元素(“左孩子最右边的节点”或“右孩子最左边的节点”)到父节点中,然后是移动之后的情况;如果没有,直接删除。
- 某结点中元素数目小于(m/2)-1,(m/2)向上取整,则需要看其某相邻兄弟结点是否丰满;
- 如果丰满(结点中元素个数大于(m/2)-1),则向父节点借一个元素来满足条件;
- 如果其相邻兄弟都不丰满,即其结点数目等于(m/2)-1,则该结点与其相邻的某一兄弟结点进行“合并”成一个结点;
接下来还以5阶B树为例,详细讲解删除的动作;
- 关键要领,元素个数小于 2(m/2 -1)就合并,大于4(m-1)就分裂
如图依次删除依次删除【8】,【20】,【18】,【5】
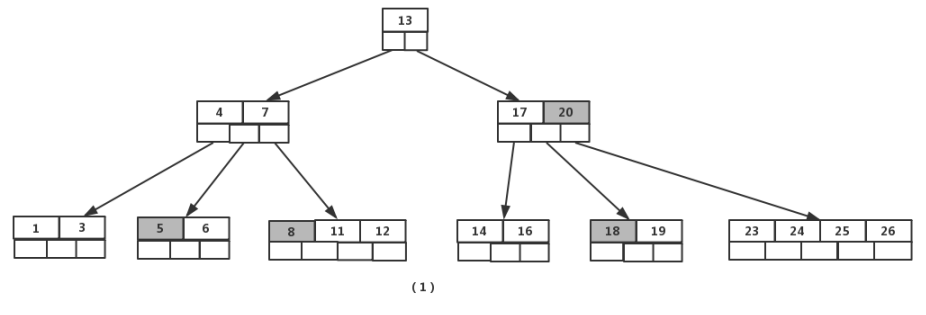
首先删除元素【8】,当然首先查找【8】,【8】在一个叶子结点中,删除后该叶子结点元素个数为2,符合B树规则,操作很简单,咱们只需要移动【11】至原来【8】的位置,移动【12】至【11】的位置(也就是结点中删除元素后面的元素向前移动)

下一步,删除【20】,因为【20】没有在叶子结点中,而是在中间结点中找到,咱们发现他的继承者【23】(字母升序的下个元素),将【23】上移到【20】的位置,然后将孩子结点中的【23】进行删除,这里恰好删除后,该孩子结点中元素个数大于2,无需进行合并操作。

下一步删除【18】,【18】在叶子结点中,但是该结点中元素数目为2,删除导致只有1个元素,已经小于最小元素数目2,而由前面我们已经知道:如果其某个相邻兄弟结点中比较丰满(元素个数大于ceil(5/2)-1=2),则可以向父结点借一个元素,然后将最丰满的相邻兄弟结点中上移最后或最前一个元素到父节点中,在这个实例中,右相邻兄弟结点中比较丰满(3个元素大于2),所以先向父节点借一个元素【23】下移到该叶子结点中,代替原来【19】的位置,【19】前移;然【24】在相邻右兄弟结点中上移到父结点中,最后在相邻右兄弟结点中删除【24】,后面元素前移。

最后一步删除【5】, 删除后会导致很多问题,因为【5】所在的结点数目刚好达标,刚好满足最小元素个数(ceil(5/2)-1=2),而相邻的兄弟结点也是同样的情况,删除一个元素都不能满足条件,所以需要该节点与某相邻兄弟结点进行合并操作;首先移动父结点中的元素(该元素在两个需要合并的两个结点元素之间)下移到其子结点中,然后将这两个结点进行合并成一个结点。所以在该实例中,咱们首先将父节点中的元素【4】下移到已经删除【5】而只有【6】的结点中,然后将含有【4】和【6】的结点和含有【1】,【3】的相邻兄弟结点进行合并成一个结点。

也许你认为这样删除操作已经结束了,其实不然,在看看上图,对于这种特殊情况,你立即会发现父节点只包含一个元素【7】,没达标(因为非根节点包括叶子结点的元素K必须满足于2=<K<=4,而此处的K=1),这是不能够接受的。如果这个问题结点的相邻兄弟比较丰满,则可以向父结点借一个元素。而此时兄弟节点元素刚好为2,刚刚满足,只能进行合并,而根结点中的唯一元素【13】下移到子结点,这样,树的高度减少一层。

看完插入,删除,想必也把B树的特征掌握了,下面普及下其他知识,换个脑子
磁盘IO与预读
计算机存储设备一般分为两种:内存储器(main memory)和外存储器(external memory)。
内存储器为内存,内存存取速度快,但容量小,价格昂贵,而且不能长期保存数据(在不通电情况下数据会消失)。
外存储器即为磁盘读取,磁盘读取数据靠的是机械运动,每次读取数据花费的时间可以分为寻道时间、旋转延迟、传输时间三个部分,寻道时间指的是磁臂移动到指定磁道所需要的时间,主流磁盘一般在5ms以下;旋转延迟就是我们经常听说的磁盘转速,比如一个磁盘7200转,表示每分钟能转7200次,也就是说1秒钟能转120次,旋转延迟就是1/120/2 = 4.17ms;传输时间指的是从磁盘读出或将数据写入磁盘的时间,一般在零点几毫秒,相对于前两个时间可以忽略不计。那么访问一次磁盘的时间,即一次磁盘IO的时间约等于5+4.17 = 9ms左右,听起来还挺不错的,但要知道一台500 -MIPS的机器每秒可以执行5亿条指令,因为指令依靠的是电的性质,换句话说执行一次IO的时间可以执行40万条指令,数据库动辄十万百万乃至千万级数据,每次9毫秒的时间,显然是个灾难。下图是计算机硬件延迟的对比图,供大家参考:

考虑到磁盘IO是非常高昂的操作,计算机操作系统做了一些优化,当一次IO时,不光把当前磁盘地址的数据,而是把相邻的数据也都读取到内存缓冲区内,因为局部预读性原理告诉我们,当计算机访问一个地址的数据的时候,与其相邻的数据也会很快被访问到。每一次IO读取的数据我们称之为一页(page)。具体一页有多大数据跟操作系统有关,一般为4k或8k,也就是我们读取一页内的数据时候,实际上才发生了一次IO,这个理论对于索引的数据结构设计非常有帮助。
事实1 : 不同容量的存储器,访问速度差异悬殊。
- 磁盘(ms级别) << 内存(ns级别), 100000倍
- 若内存访问需要1s,则一次外存访问需要一天
- 为了避免1次外存访问,宁愿访问内存100次...所以将
最常用的数据存储在最快的存储器中
事实2 : 从磁盘中读 1 B,与读写 1KB 的时间成本几乎一样
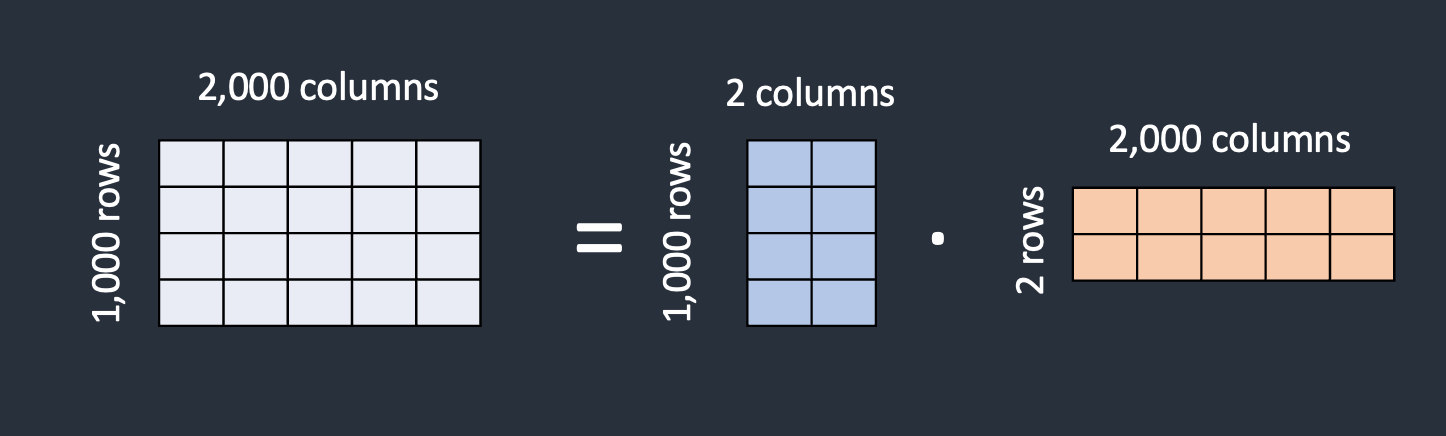
从以上数据中可以总结出一个道理,索引查询的数据主要受限于硬盘的I/O速度,查询I/O次数越少,速度越快,所以B树的结构才应需求而生;B树的每个节点的元素可以视为一次I/O读取,树的高度表示最多的I/O次数,在相同数量的总元素个数下,每个节点的元素个数越多,高度越低,查询所需的I/O次数越少;假设,一次硬盘一次I/O数据为8K,索引用int(4字节)类型数据建立,理论上一个节点最多可以为2000个元素,2000*2000*2000=8000000000,80亿条的数据只需3次I/O(理论值),可想而知,B树做为索引的查询效率有多高;
另外也可以看出同样的总元素个数,查询效率和树的高度密切相关
B树的高度
一棵含有N个总关键字数的m阶的B树的最大高度是多少?
log(m/2)(N+1)/2 + 1 ,log以(m/2)为低,(N+1)/2的对数再加1
算法如下

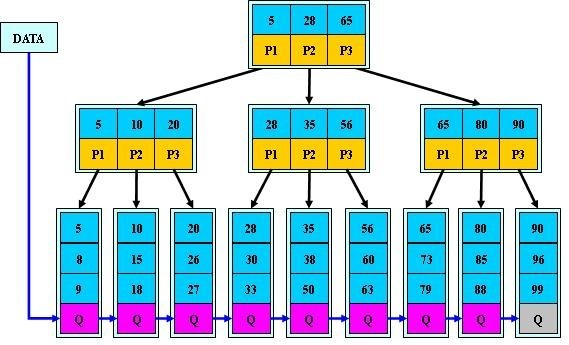
B+树
B+树是应文件系统所需而产生的B树的变形树,那么可能一定会想到,既然有了B树,又出一个B+树,那B+树必然是有很多优点的
B+树的特征:
- 有m个子树的中间节点包含有m个元素(B树中是k-1个元素),每个元素不保存数据,只用来索引;
- 所有的叶子结点中包含了全部关键字的信息,及指向含有这些关键字记录的指针,且叶子结点本身依关键字的大小自小而大的顺序链接。 (而B 树的叶子节点并没有包括全部需要查找的信息);
- 所有的非终端结点可以看成是索引部分,结点中仅含有其子树根结点中最大(或最小)关键字。 (而B 树的非终节点也包含需要查找的有效信息);
查找算法
查找以典型的方式进行,类似于二叉查找树。起始于根节点,自顶向下遍历树,选择其分离值在要查找值的任意一边的子指针。在节点内部典型的使用是二分查找来确定这个位置。
对B+树可以进行两种查找运算:
1、从最小关键字起顺序查找;
2、从根结点开始,进行随机查找。
在查找时,若非终端结点上的关键值等于给定值,并不终止,而是继续向下直到叶子结点。因此,在B+树中,不管查找成功与否,每次查找都是走了一条从根到叶子结点的路径。其余同B-树的查找类似。
插入算法
m阶B树的插入操作在叶子结点上进行,假设要插入关键值a,找到叶子结点后插入a,做如下算法判别:
①如果当前结点是根结点并且插入后结点关键字数目小于等于m,则算法结束;
②如果当前结点是非根结点并且插入后结点关键字数目小于等于m,则判断若a是新索引值时转步骤④后结束,若a不是新索引值则直接结束;
③如果插入后关键字数目大于m(阶数),则结点先分裂成两个结点X和Y,并且他们各自所含的关键字个数分别为:u=大于(m+1)/2的最小整数,v=小于(m+1)/2的最大整数;
由于索引值位于结点的最左端或者最右端,不妨假设索引值位于结点最右端,有如下操作:
如果当前分裂成的X和Y结点原来所属的结点是根结点,则从X和Y中取出索引的关键字,将这两个关键字组成新的根结点,并且这个根结点指向X和Y,算法结束;
如果当前分裂成的X和Y结点原来所属的结点是非根结点,依据假设条件判断,如果a成为Y的新索引值,则转步骤④得到Y的双亲结点P,如果a不是Y结点的新索引值,则求出X和Y结点的双亲结点P;然后提取X结点中的新索引值a’,在P中插入关键字a’,从P开始,继续进行插入算法;
④提取结点原来的索引值b,自顶向下,先判断根是否含有b,是则需要先将b替换为a,然后从根结点开始,记录结点地址P,判断P的孩子是否含有索引值b而不含有索引值a,是则先将孩子结点中的b替换为a,然后将P的孩子的地址赋值给P,继续搜索,直到发现P的孩子中已经含有a值时,停止搜索,返回地址P。
删除算法
B+树的删除也仅在叶子结点进行,当叶子结点中的最大关键字被删除时,其在非终端结点中的值可以作为一个“分界关键字”存在。若因删除而使结点中关键字的个数少于m/2(m/2结果取上界,如5/2结果为3)时,其和兄弟结点的合并过程亦和B-树类似。
1、首先,查找要删除的值。接着从包含它的节点中删除这个值。
2、如果没有节点处于违规状态则处理结束。
3、如果节点处于违规状态则有两种可能情况:
(1)它的兄弟节点,就是同一个父节点的子节点,可以把一个或多个它的子节点转移到当前节点,而把它返回为合法状态。如果是这样,在更改父节点和两个兄弟节点的分离值之后处理结束。
(2)它的兄弟节点由于处在低边界上而没有额外的子节点。在这种情况下把两个兄弟节点合并到一个单一的节点中,而且我们递归到父节点上,因为它被删除了一个子节点。持续这个处理直到当前节点是合法状态或者到达根节点,在其上根节点的子节点被合并而且合并后的节点成为新的根节点。
算法区分
B+树与B-树
B+树是应文件系统所需而产生的一种B-树的变形树。一棵m阶的B+树和m阶的B树的差异在于:
(1)有n棵子树的结点中含有n个关键码;
(2)所有的叶子结点中包含了全部关键码的信息,及指向含有这些关键码记录的指针,且叶子结点本身依关键码的大小自小而大的顺序链接;
(3)所有的非终端结点可以看成是索引部分,结点中仅含有其子树根结点中最大(或最小)关键码。
为什么说B+树比B树更适合数据库索引?
1)B+树的磁盘读写代价更低
B+树的内部结点并没有指向关键字具体信息的指针。因此其内部结点相对B 树更小。如果把所有同一内部结点的关键字存放在同一盘块中,那么盘块所能容纳的关键字数量也越多。一次性读入内存中的需要查找的关键字也就越多。相对来说IO读写次数也就降低了;
2)B+树查询效率更加稳定
由于非终结点并不是最终指向文件内容的结点,而只是叶子结点中关键字的索引。所以任何关键字的查找必须走一条从根结点到叶子结点的路。所有关键字查询的路径长度相同,导致每一个数据的查询效率相当;
3)B+树便于范围查询(最重要的原因,范围查找是数据库的常态)
B树在提高了IO性能的同时并没有解决元素遍历的我效率低下的问题,正是为了解决这个问题,B+树应用而生。B+树只需要去遍历叶子节点就可以实现整棵树的遍历。而且在数据库中基于范围的查询是非常频繁的,而B树不支持这样的操作或者说效率太低;不懂可以看看这篇解读-》范围查找
补充:B树的范围查找用的是中序遍历,而B+树用的是在链表上遍历;
B+树如下: