1、 线性回归的原理
1.1 线性回归应用场景
房价预测
销售额度预测
金融:贷款额度预测、利用线性回归以及系数分析因子

1.2 什么是线性回归
1.2.1定义与公式
线性回归(Linear regression)是利用回归方程(函数)对一个或多个自变量(特征值)和因变量(目标值)之间关系进行建模的一种分析方式。
- 特点:只有一个自变量的情况称为单变量回归,大于一个自变量情况的叫做多元回归
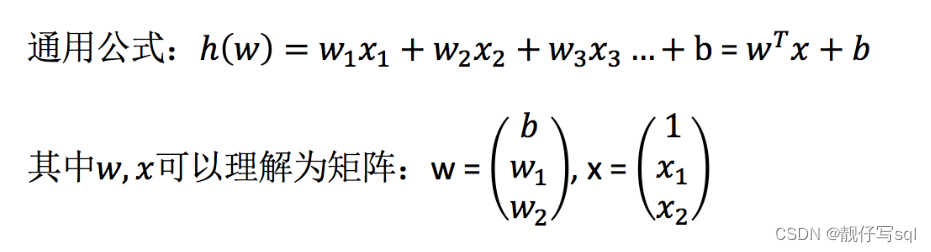
那么怎么理解呢?我们来看几个例子
期末成绩 = 0.7×考试成绩+0.3×平时成绩
房子价格 = 0.02×中心区域的距离 + 0.04×城市一氧化氮浓度 + (-0.12×自住房平均房价) + 0.254×城镇犯罪率
上面两个例子,我们看到特征值与目标值之间建立的一个关系,这个可以理解为回归方程。
1.2.2 线性回归的特征与目标的关系分析
线性回归当中的关系有两种,一种是线性关系,另一种是非线性关系。在这里我们只能画一个平面更好去理解,所以都用单个特征举例子。
- 线性关系
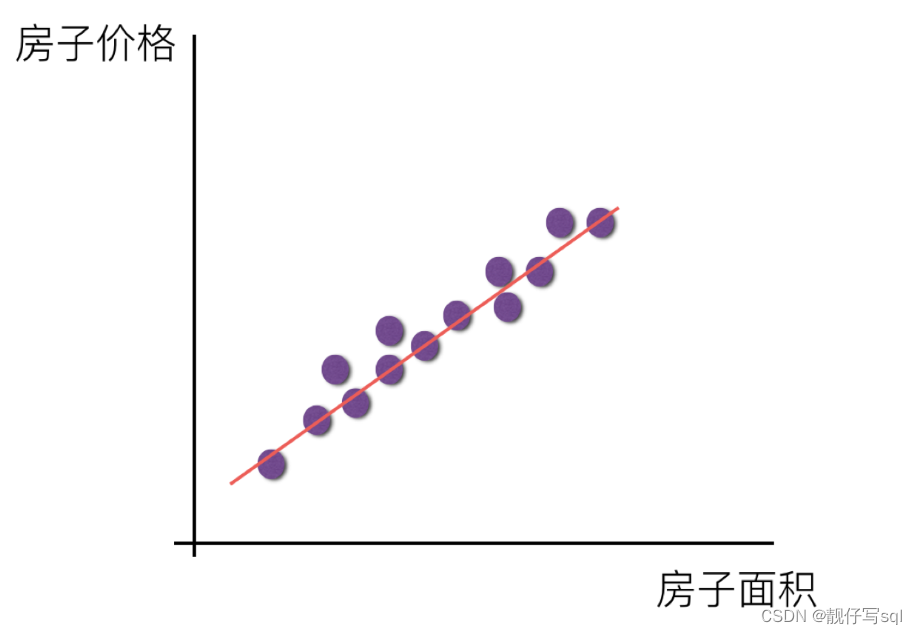
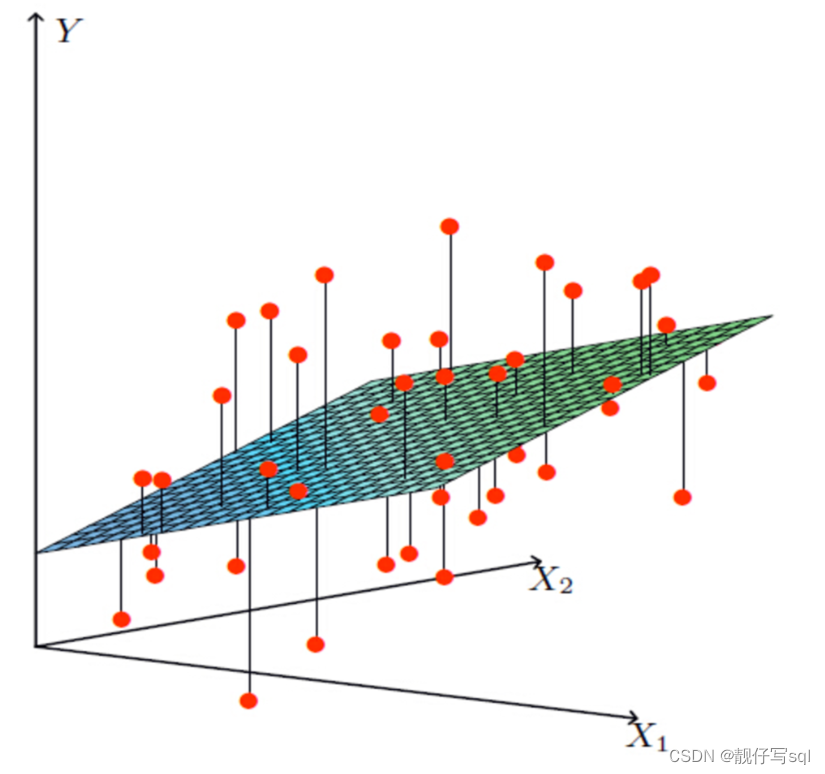
注释:如果在单特征与目标值的关系呈直线关系,或者两个特征与目标值呈现平面的关系
更高维度的我们不用自己去想,记住这种关系即可

注释:为什么会这样的关系呢?原因是什么?我们后面 讲解过拟合欠拟合重点介绍
如果是非线性关系,那么回归方程可以理解为:
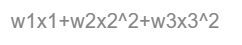
1.2.3 广义线性模型
非线性关系?
线性模型
1、自变量一次
y = w1x1 + w2x2 + w3x3 + …… + wnxn + b
2、参数一次
y = w1x1 + w2x1^2 + w3x1^3 + w4x2^3 + …… + b
1.2.4 线性关系&线性模型
1、线性关系一定是线性模型
2、线性模型不一定是线性关系
2、线性回归的损失函数和优化原理(理解记忆)
假设刚才的房子例子,真实的数据之间存在这样的关系
真实关系:真实房子价格 = 0.02×中心区域的距离 + 0.04×城市一氧化氮浓度 + (-0.12×自住房平均房价) + 0.254×城镇犯罪率
那么现在呢,我们随意指定一个关系(猜测)
随机指定关系:预测房子价格 = 0.25×中心区域的距离 + 0.14×城市一氧化氮浓度 + 0.42×自住房平均房价 + 0.34×城镇犯罪率
请问这样的话,会发生什么?真实结果与我们预测的结果之间是不是存在一定的误差呢?类似这样样子
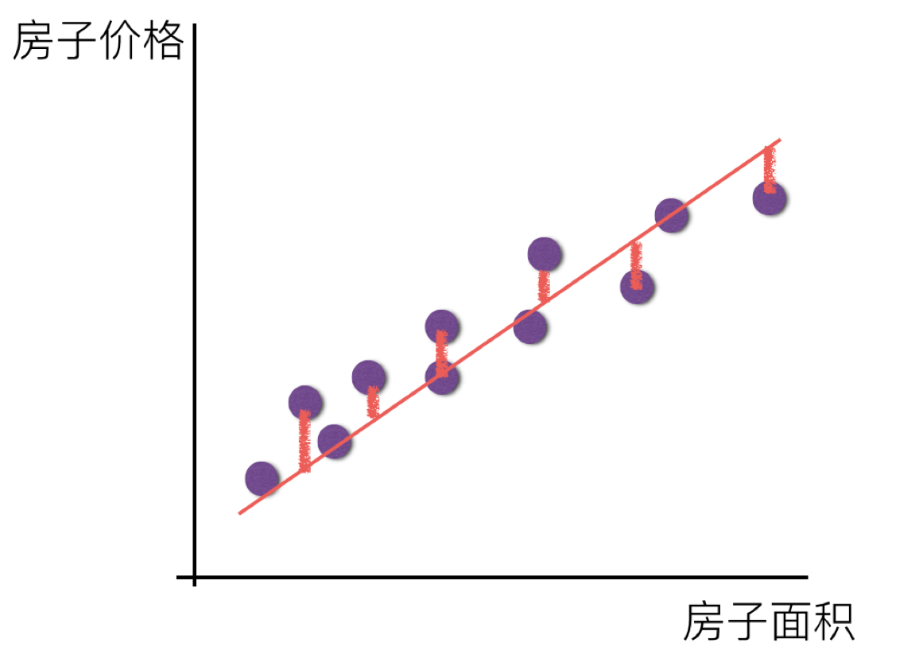
那么存在这个误差,我们将这个误差给衡量出来。
2.1 损失函数
总损失定义为:

如何去减少这个损失,使我们预测的更加准确些?既然存在了这个损失,我们一直说机器学习有自动学习的功能,在线性回归这里更是能够体现。这里可以通过一些优化方法去优化(其实是数学当中的求导功能)回归的总损失!!!
2.2 优化算法
如何去求模型当中的W,使得损失最小?(目的是找到最小损失对应的W值)
线性回归经常使用的两种优化算法
-
优化方法?
-
正规方程
- 天才 - 直接求解W
拓展:
1)求导,得到最大最小值:
y = ax^2 + bx + c
y’ = 2ax + b = 0
x = - b / 2a
2)矩阵逆计算:
a * b = 1
b = 1 / a = a ^ -1
A * B = E
[[1, 0, 0],
[0, 1, 0],
[0, 0, 1]]
B = A ^ -1
- 天才 - 直接求解W
-
梯度下降
勤奋努力的普通人
试错、改进
-
-
正规方程
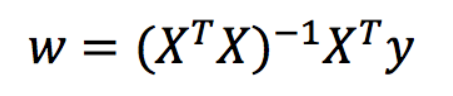
理解:X为特征值矩阵,y为目标值矩阵。直接求到最好的结果
缺点:当特征过多过复杂时,求解速度太慢并且得不到结果