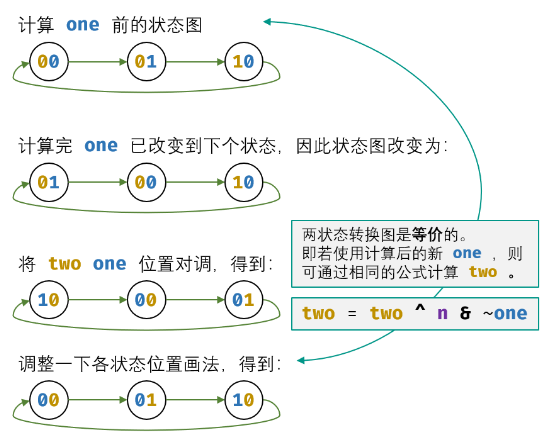
Python数据结构（顺序表）

时间复杂度排序

O(1)< O(logn)< O(n)< O(nlogn)< O(n^2)< O(n^3)< O(2^n)< O(n!)< O(n^n)

顺序表的形式

图a表示的是顺序表的基本形式，数据元素本身连续存储，每个元素所占的存储单元大小固定相同，元素

的下标是其逻辑地址，而元素存储的物理地址 (实际内存地址)可以通过存储区的起始地址Loc(e0)加上逻

辑地址(第i个元素)与存储单元大小©的乘积计算而得，即:

Loc(ei) = Loc(e0)+ ci

故，访问指定元素时无需从头遍历，通过计算便可获得对应地址，其时间复杂度为O(1)。

如果元素的大小不统一，则须采用图b的元素外置的形式，将实际数据元素另行存储，而顺序表中各单元

位置保存对应元素的地址信息(即链接)。由于每个链接所需的存储量相同，通过上述公式，可以计算出元

素链接的存储位置，而后顺着链接找到实际存储的数据元素。注意，图b中的c不再是数据元素的大小，

而是存储一个链接地址所需的存储量，这个量通常很小。

图b这样的顺序表也被称为对实际数据的索引，这是最简单的索引结构

顺序表的结构与实现

顺序表的结构

一个顺序表的完整信息包括两部分，一部分是表中的元素集合，另一部分是为实现正确操作而需记录的

信息，即有关表的整体情况的信息，这部分信息主要包括元素存储区的容量和当前表中已有的元素个数

两项.

顺序表的两种基本实现

图a为一体式结构，存储表信息的单元与元素存储区以连续的方式安排在一块存储区里，两部分数据的整

体形成一个完整的顺序表对象。

一体式结构整体性强，易于管理。但是由于数据元素存储区域是表对象的一部分，顺序表创建后，元素

存储区就固定了。

图b为分离式结构，表对象里只保存与整个表有关的信息(即容量和元素个数)，实际数据元素存放在另一

个独立的元素存储区里，通过链接与基本表对象关联

元素存储区替换

一体式结构由于顺序表信息区与数据区连续存储在一起，所以若想更换数据区，则只能整体搬迁，即整

个顺序表对象(指存储顺序表的结构信息的区域)改变了。

分离式结构若想更换数据区，只需将表信息区中的数据区链接地址更新即可，而该顺序表对象不变

元素存储区扩充

采用分离式结构的顺序表，若将数据区更换为存储空间更大的区域，则可以在不改变表对象的前提下对

其数据存储区进行了扩充，所有使用这个表的地方都不必修改。只要程序的运行环境(计算机系统)还有空

闲存储，这种表结构就不会因为满了而导致操作无法进行。人们把采用这种技术实现的顺序表称为动态

顺序表，因为其容量可以在使用中动态变化。

扩充的两种策略

​ 每次扩充增加固定数目的存储位置，如每次扩充增加10个元素位置，这种策略可称为线性增长。

​ 特点:节省空间，但是扩充操作频繁，操作次数多

​ 每次扩充容量加倍，如每次扩充增加一倍存储空间

​ 特点:减少了扩充操作的执行次数，但可能会浪费空间资源。以空间换时间，推荐的方式。

顺序表的操作

增加元素

如图所示，为顺序表增加新元素111的三种方式

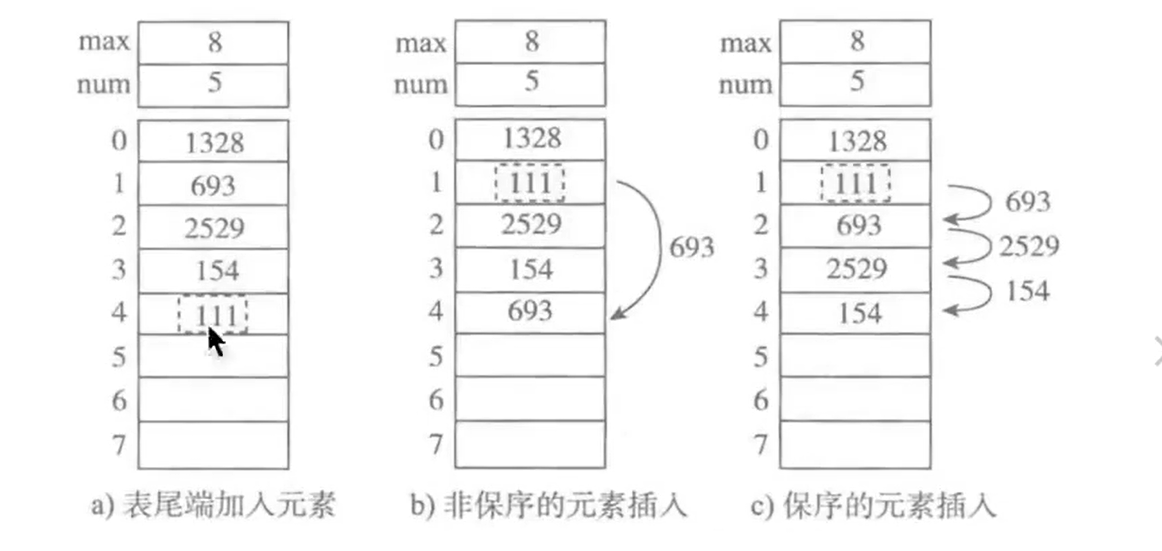
a.尾端加入元素，时间复杂度为O(1)

b.非保序的加入元素 (不常见) ，时间复杂度为O(1)

c.保序的元素加入，时间复杂度为O(n)

删除元素

a.删除表尾元素，时间复杂度为O(1)

b.非保序的元素删除(不常见)，时间复杂度为O(1)

c.保序的元素删除，时间复杂度为O(n)

Python中的顺序表

Python中的list和tuple两种类型采用了顺序表的实现技术，具有前面讨论的顺序表的所有性质tuple是不

可变类型，即不变的顺序表，因此不支持改变其内部状态的任何操作，而其他方面，则与list的性质类

似。

list的基本实现技术

Python标准类型list就是一种元素个数可变的线性表，可以加入和删除元素，并在各种操作中维持已有元

素的顺序(即保序)，而且还具有以下行为特征:

​ 基于下标(位置)的高效元素访问和更新，时间复杂度应该是O(1);

​ 为满足该特征，应该采用顺序表技术，表中元素保存在一块连续的存储区中。

​ 充许任意加入元素，而且在不断加入元素的过程中，表对象的标识(函数id得到的值)不变

​ 为满足该特征，就必须能更换元素存储区，并且为保证更换存储区时list对象的标识id不变，只能采用

​ 分离式实现技术

在Python的官方实现中，list就是一种采用分离式技术实现的动态顺序表。这就是为什么list.append(x)

(或list.insert(len(list),x)，即尾部插入) 比在指定位置插入元素效率高的原因。

在Python的官方实现中，list实现采用了如下的策略: 在建立空表(或者很小的表)时，系统分配一块能容纳

8个元素的存储区;在执行插入操作 (insert或append)时，如果元素存储区满就换一块4倍大的存储区。但

如果此时的表已经很大(目前的阀值为50000)，则改变策略，采用加一倍的方法。引入这种改变策略的方

ist实现采用了如下的策略: 在建立空表(或者很小的表)时，系统分配一块能容纳

8个元素的存储区;在执行插入操作 (insert或append)时，如果元素存储区满就换一块4倍大的存储区。但

如果此时的表已经很大(目前的阀值为50000)，则改变策略，采用加一倍的方法。引入这种改变策略的方

式，是为了避免出现过多空闲的存储位置。