今天跟大家分享华南理工大学和阿里巴巴联合提出的将ViT模型用于下游任务的高效微调方法HSN,该方法在迁移学习、目标检测、实例分割、语义分割等多个下游任务中表现优秀,性能接近甚至在某些任务上超越全参数微调。

- 论文标题:Hierarchical Side Tuning for Vision Transformers
- 机构:华南理工大学、阿里巴巴
- 论文地址:https://arxiv.org/pdf/2310.05393.pdf
- 代码地址(即将开源):https://github.com/AFeng-x/HST#hierarchical-side-tuning-for-vision-transformers
- 关键词:Vision Transformer、迁移学习、目标检测、实例分割、语义分割
1.动机
近年来,大规模的Vision Transformer(简称ViT)在多个任务中表现优秀,很多研究人员尝试利用ViT中的预训练知识提升下游任务的性能。然而,快速增长的模型规模使得在开发下游任务时直接微调预训练模型变得不切实际。 Parameter-efficient transfer learning(简称PETL)方法通过选择预训练模型的参数子集或在主干中引入有限数量的可学习参数,同时保持大部分原始参数不变,来解决该问题。
尽管PETL方法取得了重大成功,但主要是为识别任务而设计的。当将其用于密集预测任务时(比如目标检测和分割),与完全的微调相比其性能仍有很大的差距,这可能是由于密集预测任务与分类任务有本质上的不同。为了解决这一性能差距,作者提出了一种更通用的PETL方法Hierarchical Side-Tuning(简称HST),作者构建了Hierarchical Side Network(简称HSN),能产生金字塔式的多尺度输出,使得整个模型能适应不同的任务。
2.Hierarchical Side-Tuning(HST)
2.1 HST总体结构
HST的总体结构如下图所示:
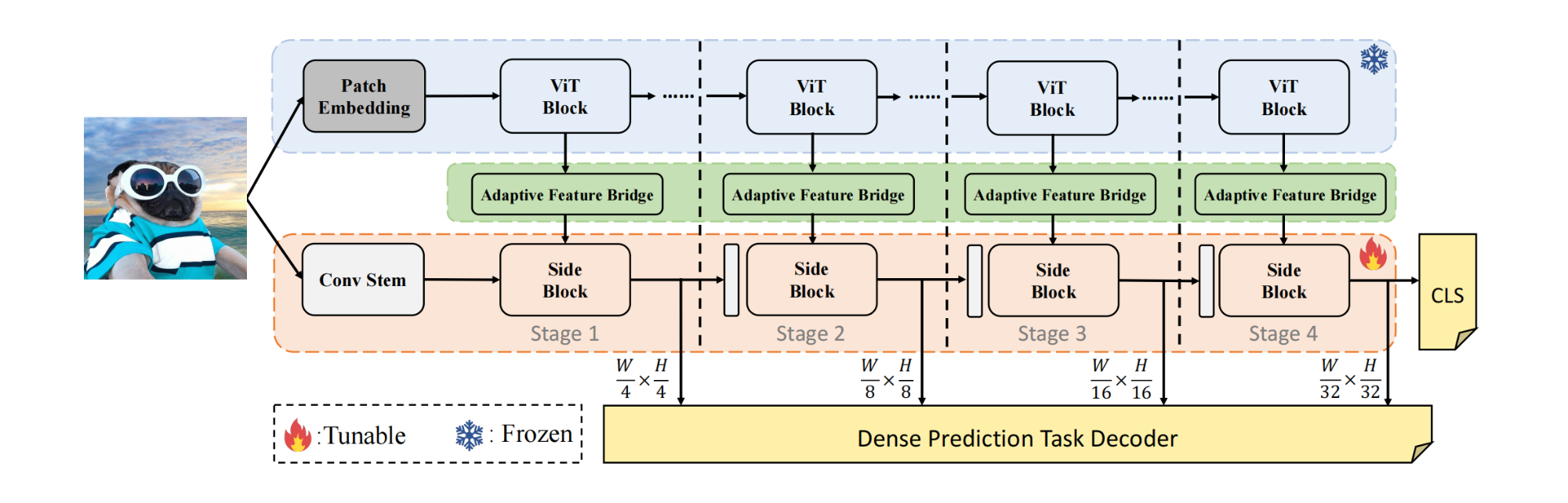
上图中蓝色部分为普通的ViT,其权重被冻结;绿色部分为Adaptive Feature Bridge(简称AFB),用于桥接和预处理中间特征;粉色部分是Hierarchical Side Network(简称HSN),由1个Conv Stem和 L L L个Side Block组成。
对于ViT部分,输入图像首先通过patch embedding,然后进入 L L L个Transformer encoder;对于HSN部分,输入图像通过Conv Stem,从输入图像中引入局部空间上下文信息。HSN由4个stage组成,下采样率分别为 { 4 , 8 , 16 , 32 } \{4,8,16,32\} {4,8,16,32},输出4种不同尺度的特征。每个Transformer encoder都有1个对应的Side Block,信息流从backbone流向Side Block。
2.2 Meta Token
与其他prompt-based的微调方法不同,作者令prompt的数量为1,并将其称作Meta Token(简称MetaT),其结构如下图所示:

作者并没有丢弃prompt对应的输出特征,而是将其与输出的patch token一起作为Adaptive Feature Bridge的输入。由于MetaT的输出特征分布与patch token的分布有差异,这会影响HSN的性能,因此要微调Transformer中的Layer Normalization(简称LN)层,以改变特征的均值和方差(即改变了特征分布),有助于保持同一样本中不同特征之间的相对值。下图展示了MetaT的输出特征与ViT中patch token之间的余弦相似度,显然,通过微调LN层,MetaT的输出与patch token的向量方向能更好地对齐,从而有效地利用MetaT的输出特征。

2.3 Adaptive Feature Bridge(AFB)
由于ViT的输出特征与HSN中的特征形状不同,因此引入了Adaptive Feature Bridge(AFB),AFB包括2个重要部分:双分支分离(Dual-Branch Separation)和权重共享(Linear Weight Sharing),如下图所示:

Dual-Branch Separation
MetaT的输出和patch token先经过线性层进行维度变换,线性层的输出分为2个分支,patch token进行全局平均池化输出1个token,将其称作GlobalT,GlobalT与MetaT拼接得到 F m g i \mathcal{F}_{m g}^i Fmgi。通过双线性差值改变patch token的形状,使其与HSN中对应stage的特征形状一致。整体流程表示如下:
F m g i = [ W j F MetaT i , AvgPooling ( W j F patch i ) ] ; F f g i = T ( W j F v i t i ) \mathcal{F}_{m g}^i=\left[W_j \mathcal{F}_{\text {MetaT }}^i, \operatorname{AvgPooling}\left(W_j \mathcal{F}_{\text {patch }}^i\right)\right] ; \mathcal{F}_{f g}^i=\mathcal{T}\left(W_j \mathcal{F}_{v i t}^i\right) Fmgi=[WjFMetaT i,AvgPooling(WjFpatch i)];Ffgi=T(WjFviti)
上式中 i i i表示第 i i i个Vit block, W j W_j Wj表示第 j j j个stage中线性层的权重矩阵。
Linear Weight Sharing
同一个stage中的多个AFB共享线性层权重,以减少可学习参数;此外,这样能在同一个stage中实现特征间的信息交互,达到与使用多个线性层相当的效果。
2.4 Side Block
Side Block包含1个cross-attention层和1个Feed-Forward Network(简称FFN),其结构如下图所示。

Side Block对ViT的中间特征和多尺度特征进行建模,考虑到这两个输入分支的特点,作者通过不同的方法将它们引入到Side Block中。
Meta-Global Injection
将HSN输出的多尺度特征作为Query(记作 Q Q Q),使用meta-global token作为key(记作 K K K)和value(记作 V V V),cross-attention表示如下:
( ( Q h s n ) ( K m g ) T ) V m g = A V m g \left(\left(Q_{h s n}\right)\left(K_{m g}\right)^T\right) V_{m g}=A V_{m g} ((Qhsn)(Kmg)T)Vmg=AVmg
上式中 Q h s n ∈ R L × d Q_{h s n} \in \mathbb{R}^{L \times d} Qhsn∈RL×d, ( K m g ) T ∈ R d × M \left(K_{m g}\right)^T \in \mathbb{R}^{d \times M} (Kmg)T∈Rd×M, V m g ∈ R M × d V_{m g} \in \mathbb{R}^{M \times d} Vmg∈RM×d, L L L表示多尺度特征输入序列的长度, M M M表示meta-global token的长度, d d d表示特征维度。
将Meta-Global Injection的输出记作 F ^ h s n i \hat{F}_{h s n}^i F^hsni,可表示如下:
F ^ h s n i = F h s n i + CrossAttention ( F h s n i , F m g i ) \hat{\mathcal{F}}_{h s n}^i=\mathcal{F}_{h s n}^i+\operatorname{CrossAttention}\left(\mathcal{F}_{h s n}^i, \mathcal{F}_{m g}^i\right) F^hsni=Fhsni+CrossAttention(Fhsni,Fmgi)
上式中 i i i表示HST和ViT的第 i i i个block。
Fine-Grained Injection
将Meta-Global Injection的输出 F ^ h s n i \hat{F}_{h s n}^i F^hsni与 F f g i F_{f g}^i Ffgi进行元素相加,然后使用FFN进行建模,表示如下:
F h s n i + 1 = F ^ h s n i + F f g i + FFN ( F ^ h s n i + F f g i ) F_{h s n}^{i+1}=\hat{F}_{h s n}^i+F_{f g}^i+\operatorname{FFN}\left(\hat{F}_{h s n}^i+F_{f g}^i\right) Fhsni+1=F^hsni+Ffgi+FFN(F^hsni+Ffgi)
F h s n i + 1 F_{h s n}^{i+1} Fhsni+1作为下一个Side Block的输入。
3.实验
3.1 实验设置


3.2 实验结果
(1)图像分类
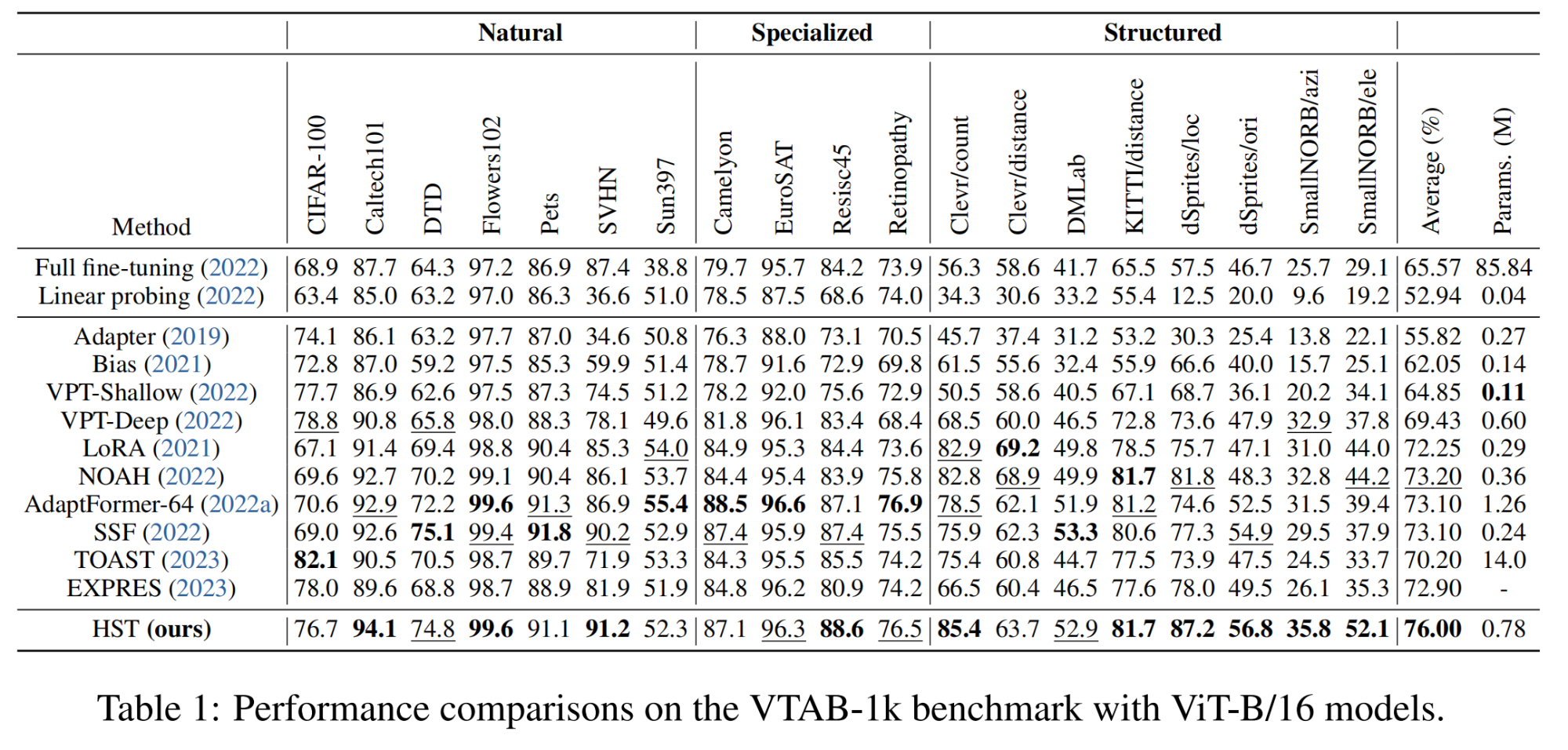
(2)目标检测和实例分割
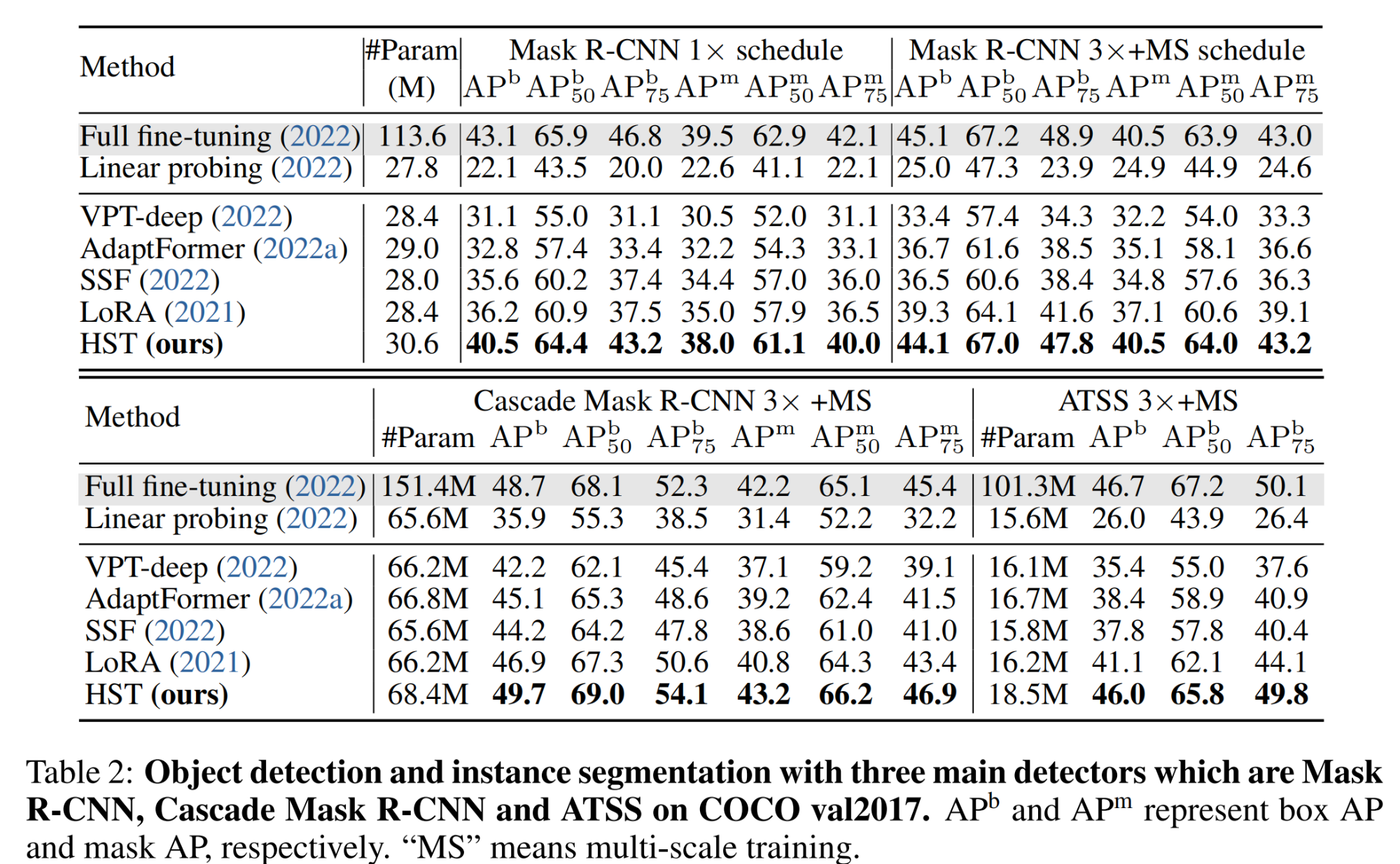
(3)语义分割
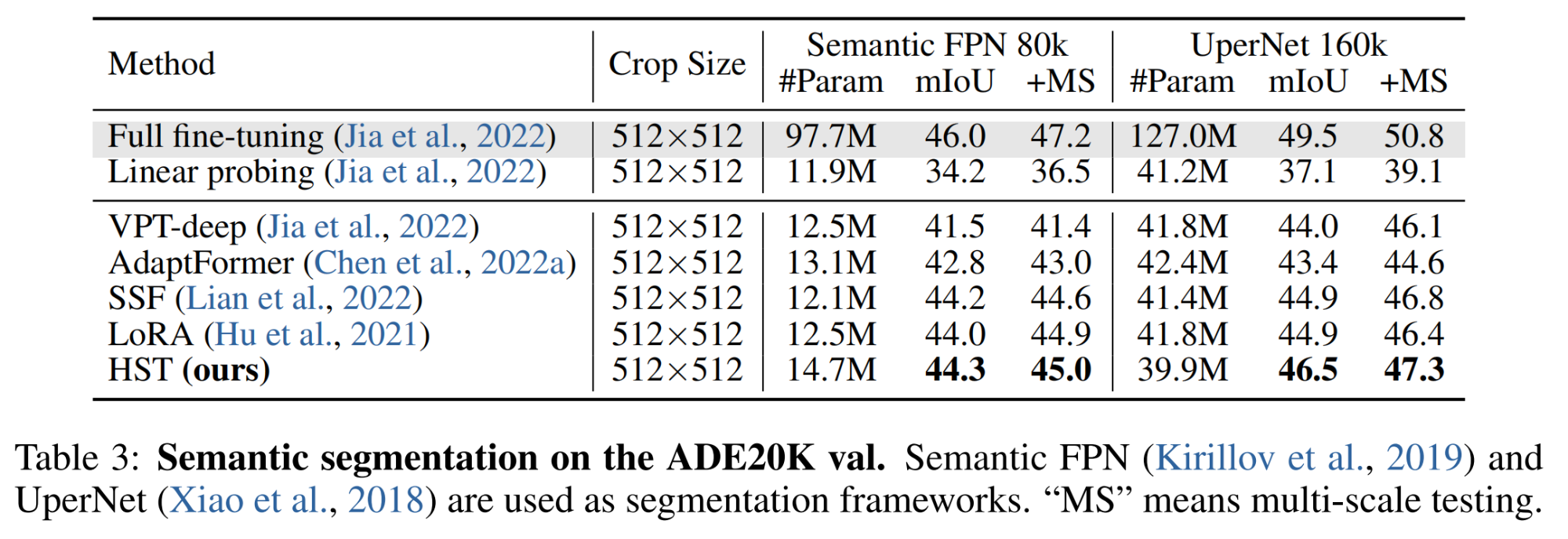
更多消融实验及分析请查看原文。
4.总结
作者提出了一种新的参数高效的迁移学习方法Hierarchical Side-Tuning(HST),可训练的side network利用了backbone的中间特征,并生成了用于进行预测的多尺度特性。通过实验表明,HST在不同的数据集和任务中表现优异,显著地减少了在密集预测任务中PETL与完全微调的性能差距。






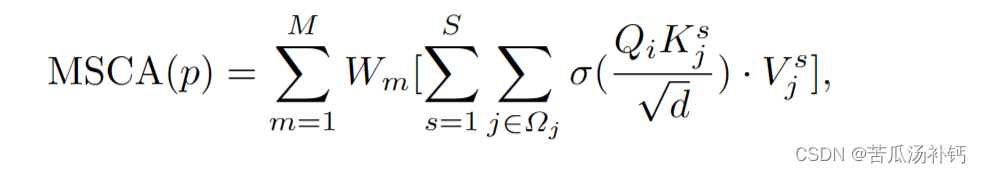

![[计算机提升] 用户和用户组](https://img-blog.csdnimg.cn/fe1b6e3065cb4bcd88a855cc5969b41a.png)