目录

前言

堆的概念与结构

堆的实现

 堆的初始化

堆的销毁

堆的显示

堆的插入

堆的向上调整算法

堆的删除

堆的向下调整算法

堆的判空

获取堆顶元素

 堆的数据个数

堆的创建

---

前言

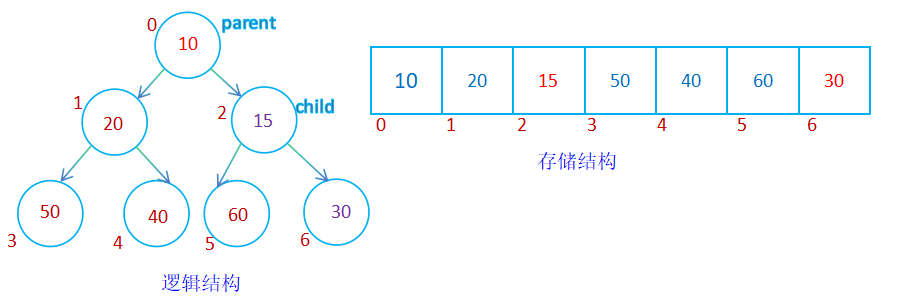
二叉树的顺序结构存储即使用数组存储，而数组存储适用于完全二叉树，完全二叉树不会存在空间上的浪费，二叉树的顺序存储在物理上是一个数组，在逻辑上是一颗二叉树；

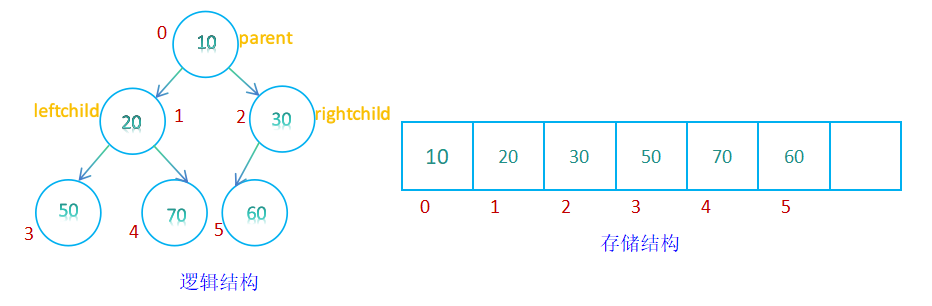
完全二叉树的顺序存储可以根据下标寻找孩子结点或者父结点，规律如下：

leftchild=2*parent+1,   rightchild=2*parent+2；

parent=(child-1)/2 ；

堆的概念与结构

堆的定义：

如果有一个关键码的集合K = {K1 ，K2 ，K3 ，…，Kn-1}，把它的所有元素按完全二叉树的顺序存储方式存储在一个一维数组中，并满足：Ki <=K2i+1且Ki<=K2i+2(Ki >= K2i+1且Ki >= K2i+2) i = 0，1， 2…，则称为小堆(或大堆)。将根节点最大的堆叫做最大堆或大根堆，根节点最小的堆叫做最小堆或小根堆；

堆的性质：

• 堆中某个节点的值总是不大于或不小于其父节点的值；
• 堆总是一棵完全二叉树；

• 小根堆示意图

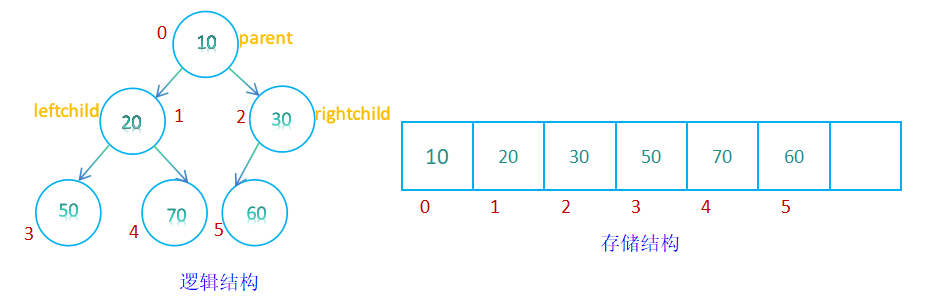
• 大根堆示意图

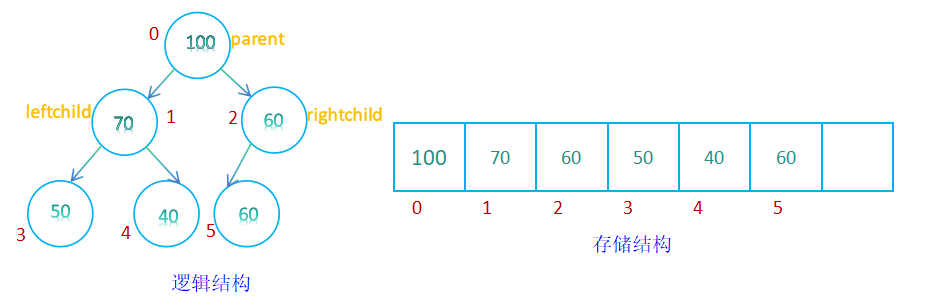
堆的实现

 堆总是一棵完全二叉树，堆是用数组存储的；

//堆结构的定义
//由于是顺序存储，采用顺序表定义
typedef int HeapDataType;
typedef struct Heap
{HeapDataType* nums;//数组int size;//数据个数int capacity;//记录数组容量
}Heap;

 堆的初始化

//堆的初始化
void HeapInit(Heap* php)
{assert(php != NULL);php->nums = (HeapDataType*)malloc(sizeof(HeapDataType)*4);if (php->nums == NULL){perror("malloc failed:");exit(-1);}php->size = 0;php->capacity = 4;
}

堆的销毁

void HeapDestroy(Heap* php)
{assert(php != NULL);free(php->nums);php->nums = NULL;php->size = 0;php->capacity = 0;
}

堆的显示

//堆的显示
void HeapPrint(Heap* php)
{assert(php != NULL);for (int i = 0; i < php->size; i++){printf("%d ", php->nums[i]);}printf("\n");
}

堆的插入

堆的插入是在堆尾的下一个位置插入数据并保证数组的逻辑结构为堆；

• case 1:

当在数组尾元素的下一个位置插入的数据其值大于等于父节点的值时，仍然为小堆；

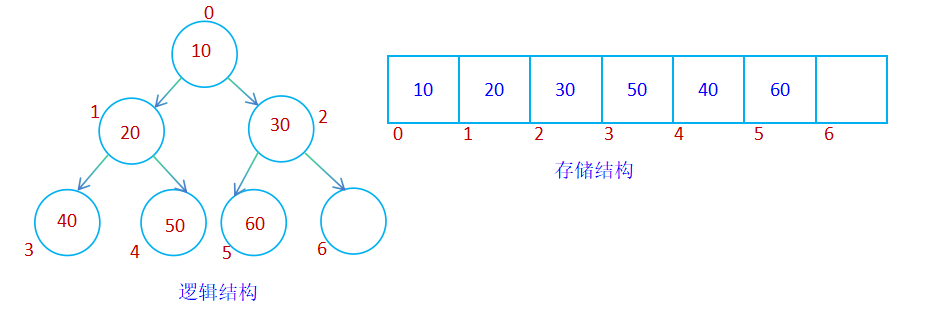
• case 2:

当在数组尾元素的下一个位置插入的数据其值小于父节点的值时，堆的逻辑结构被破坏，采用向上调整算法，将其调整为堆；

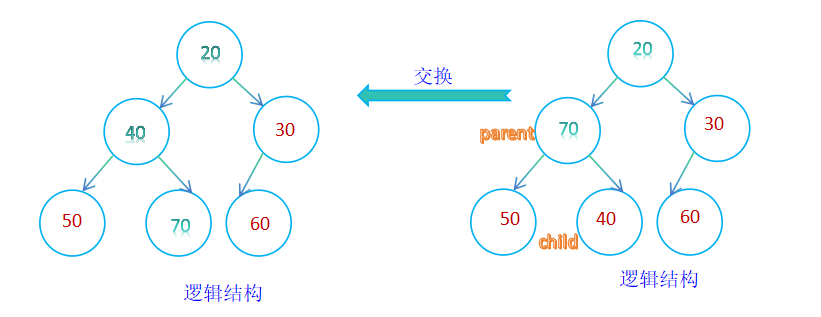
堆的向上调整算法

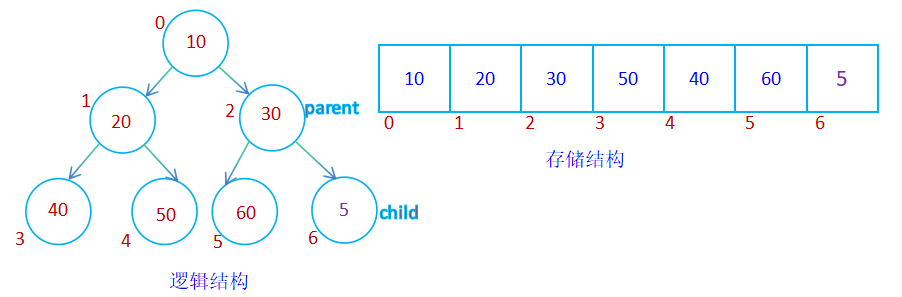
由于堆的逻辑结构为小堆，孩子结点处插入的数值小于其父节点处的值，堆的逻辑结构被破坏；首先交换child位置处与parent位置处的值，然后child=parent,parent=(child-1)/2,继续比较孩子节点与父亲结点处的数值，若不满足小堆，继续向上调整，直至根结点的位置为止或出现满足小堆的数值出现停止；

case 1:

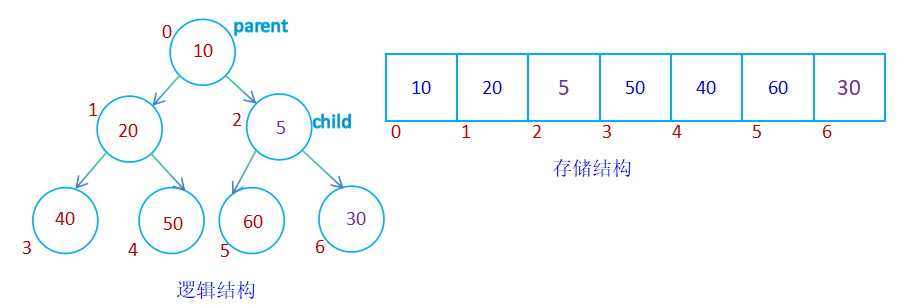
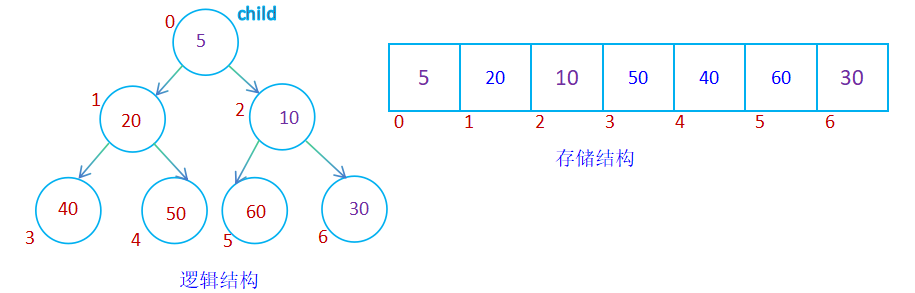
case 2:

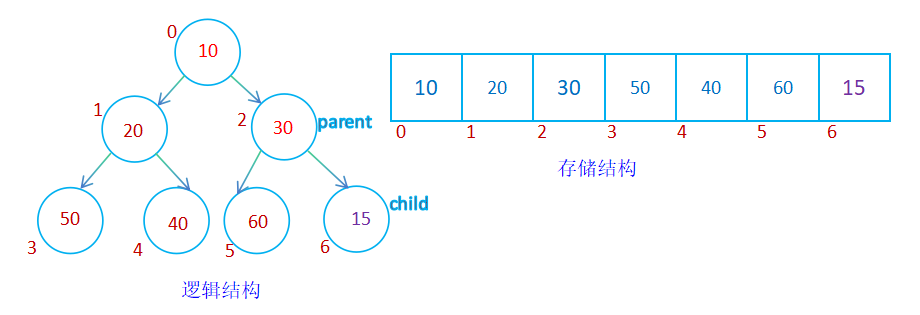
向上调整算法的时间复杂度：

当插入的数据不需要调整，时间复杂度为O(1);

当插入的数据一直调整到根结点处，调整了高度h次，设满二叉树的结点个数为N，则h=log2(N+1),那么其时间复杂度为O(logn);

综上所述，时间复杂度为O(logn);

//交换
void swap(HeapDataType* p1, HeapDataType* p2)
{HeapDataType tmp = *p1;*p1 = *p2;*p2 = tmp;
}
//堆的向上调整算法
void AdjustUp(HeapDataType* nums, int child)
{int parent = (child - 1) / 2;while (child>0){if (nums[child] < nums[parent]){swap(&nums[child], &nums[parent]);child = parent;parent = (parent - 1) / 2;}else{break;}}
}

//堆的插入
void HeapPush(Heap* php, HeapDataType x)
{assert(php != NULL);//检查数组容量，容量满时扩容;if (php->size == php->capacity){HeapDataType* tmp = (HeapDataType*)realloc(php->nums, sizeof(HeapDataType)* 2 * (php->capacity));if (tmp == NULL){perror("realloc failed:");exit(-1);}php->nums = tmp;php->capacity = 2 * (php->capacity);}//插入堆的叶结点即二叉树的叶节点php->nums[php->size] = x;php->size++;//任意数据插入之后还是堆吗？//结论是否定的-->向上调整算法-->调整为堆//参数设计为指向数组首元素的指针与数组尾元素的下标，返回值为空AdjustUp(php->nums, php->size - 1);
}

堆的删除

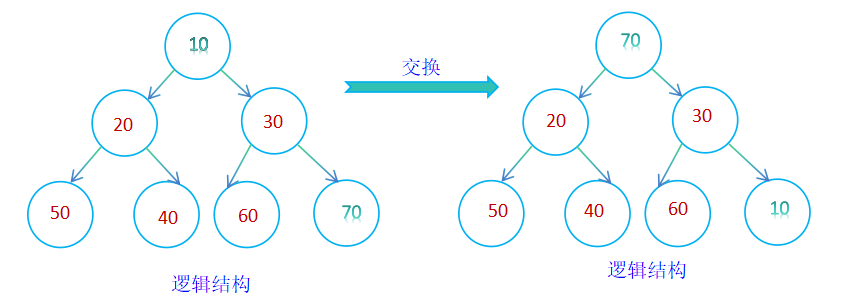
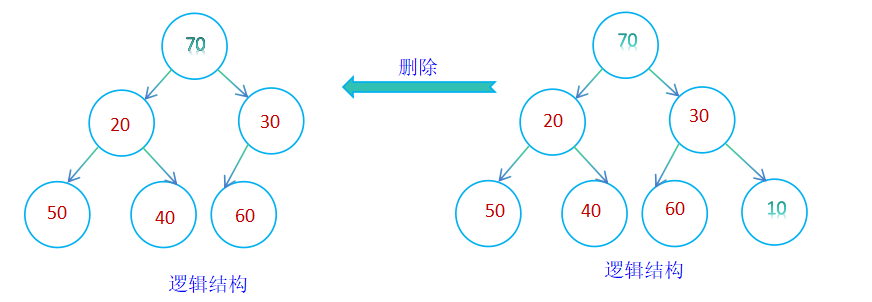
堆的删除是删除堆顶数据，并且保证其逻辑结构仍然为堆，删除的方法是将堆顶的数据与最后一个数据交换，然后删除数组最后一个数据，最后进行向下调整算法，保证其逻辑结构为堆；

堆的向下调整算法

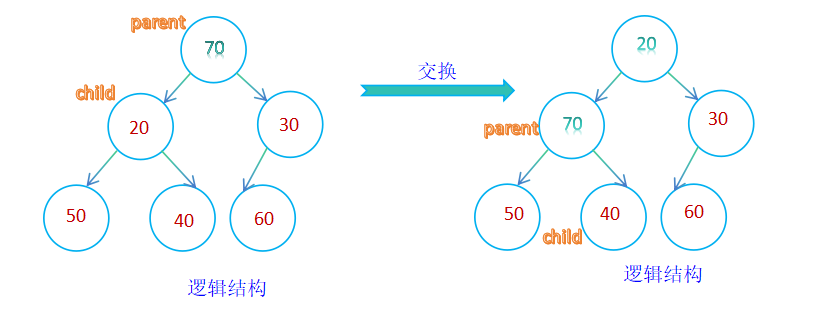
首先利用假设法寻找同一高度处值最小的孩子，根据其左右子树为小堆还是大堆，按照小堆或大堆的原则将其交换，若为小堆，父节点处的数值大于孩子结点出的数值，则交换彼此位置；若为大堆，父节点处的数值小于孩子结点出的数值，则交换彼此位置；直至叶节点为止或出现满足其逻辑上大小堆的数值为止；

堆向下调整算法的时间复杂度为O(logN)；

//堆的向下调整算法
void AdjustDown(HeapDataType* nums, int n, int parent)
{//假设法求同一深度左右孩子最小的一个,假设左孩子为最小int child = parent * 2 + 1;while (child<n){if (child+1 < n && nums[child] > nums[child + 1]){child++;}//无论左右孩子,child为最小,调整为小堆;if (nums[child] < nums[parent]){swap(&nums[child], &nums[parent]);parent = child;child = 2 * parent + 1;}else{break;}}
}

//堆的删除
void HeapPop(Heap* php)
{//删除数组首元素,并且保证逻辑为堆;assert(php != NULL);assert(php->size > 0);swap(&php->nums[0],&php->nums[php->size - 1]);php->size--;//向下调整AdjustDown(php->nums, php->size, 0);
}

堆的判空

//堆的判空
bool HeapEmpty(Heap* php)
{assert(php);return php->size == 0;
}

获取堆顶元素

//取堆顶元素
HeapDataType HeapTop(Heap* php)
{assert(php != NULL);assert(php->size > 0);return php->nums[0];
}

堆的数据个数

//堆的数据个数
int HeapSize(Heap* php)
{assert(php != NULL);return php->size;
}

堆的创建

给定一个数组，这个数组逻辑上是一颗完全二叉树，而且不一定为堆，通过向上调整算法将其构建为堆；建堆的思想为以数组首元素的下一个位置为起点，利用向上调整算法，依次插入元素建堆；

void HeapCreate(Heap* php, HeapDataType* nums, int n)
{assert(php != NULL);php->nums = (HeapDataType*)malloc(sizeof(HeapDataType)*n);if (php->nums == NULL){perror("malloc fail:");exit(-1);}php->size = php->capacity = n;memcpy(php->nums, nums, sizeof(HeapDataType)*n);//建堆，建堆的时间复杂度为O(N*logN);for (int i = 1; i < n; i++){AdjustUp(php->nums, i);}
}