文章目录
- 1. 最短路径问题
- 2. 单源最短路径--Dijkstra算法
- 算法思想
- 图解
- 如何存储路径及其权值
- 代码实现
- 调式观察
- 打印最短路径
- Dijkstra算法的缺陷
- 3. 源码
1. 最短路径问题
最短路径问题:
从带权有向图(求最短路径通常是有向图)G中的某一顶点出发,找出一条通往另一顶点的最短路径,最短也就是沿路径各边的权值总和达到最小。
那下面我们就要来学习几个求最短路径的算法
2. 单源最短路径–Dijkstra算法
这篇文章我们先来学习第一个求单源最短路径的算法——迪杰斯特拉算法(Dijkstra),是由荷兰计算机科学家狄克斯特拉于1959年提出的,然后后面我们还会学到求多源最短路径的算法。
所以这里先给大家介绍一下什么是单源最短路径,什么是多源最短路径:
单源最短路径指的是从一个源节点出发,计算到其他所有节点的最短路径。也就是说,在单源最短路径问题中,只需要确定一个起点,然后计算该起点到图中所有其他节点的最短距离。
多源最短路径则是在图中计算任意两个节点之间的最短路径。换言之,需要求解所有可能的起点和终点之间的最短路径。
那下面我们就来学习一下第一个求单源最短路径的算法——Dijkstra算法
算法思想
首先我们可以先从概念上了解一下Dijkstra算法的思想:
单源最短路径问题:给定一个图G = ( V , E ) ,求源结点s ∈ V 到图中每个结点v ∈ V的最短路径。Dijkstra算法就适用于解决带权重的有向图上的单源最短路径问题,同时算法要求图中所有边的权重非负。一般在求解最短路径的时候都是已知一个起点和一个终点,所以使用Dijkstra算法求解过后也就得到了所需起点到终点的最短路径。
针对一个带权有向图G,将所有结点分为两组S和Q,S是已经确定最短路径的结点集合,在初始时为空(初始时就可以将源节点s放入,毕竟源节点到自己的代价是0),Q 为其余未确定最短路径的结点集合,每次从Q 中找出一个从起点到该结点代价最小的结点u ,将u 从Q 中移出,并放入S 中,对u 的每一个相邻结点v (且v不在S中)进行松弛操作。松弛即对每一个相邻结点v ,判断源节点s到结点u 的代价与u 到v 的代价之和是否比原来s 到v 的代价更小,若代价比原来小则要将s 到v 的代价更新为s 到u 与u 到v 的代价之和,否则维持原样。如此一直循环直至集合Q 为空,即所有节点都已经查找过一遍并确定了最短路径,至于一些起点到达不了的结点在算法循环后其代价仍为初始设定的值,不发生变化。
Dijkstra算法每次都是选择V-S中最小的路径节点来进行更新,并加入S中,所以该算法使用的是贪心策略。
Dijkstra算法存在的问题是不支持图中带负权路径,如果带有负权路径,则可能会找不到一些路径的最短路径,这个我们后面也会给大家演示。
图解
那只看上面的概念的话,大家可能还不是特别理解,那下面我们来画图带大家分析一下
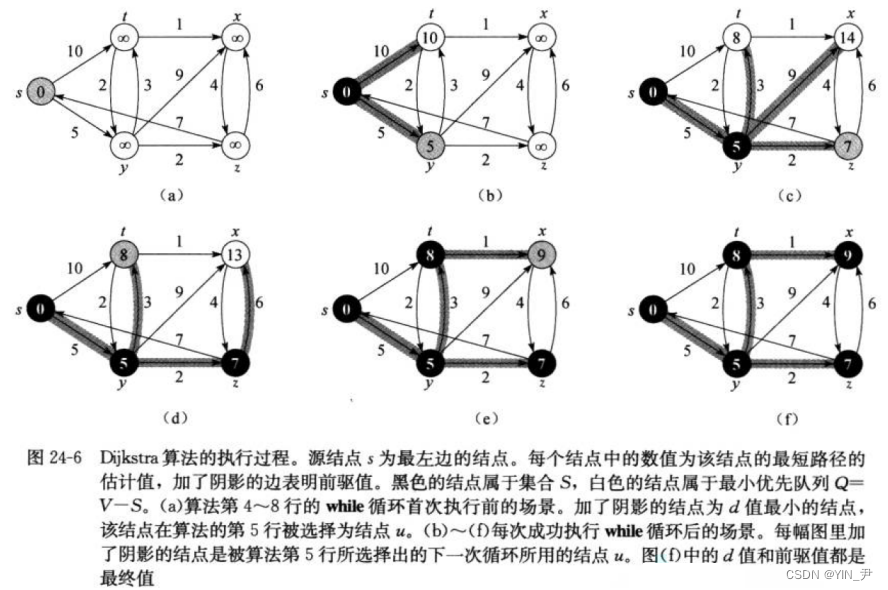
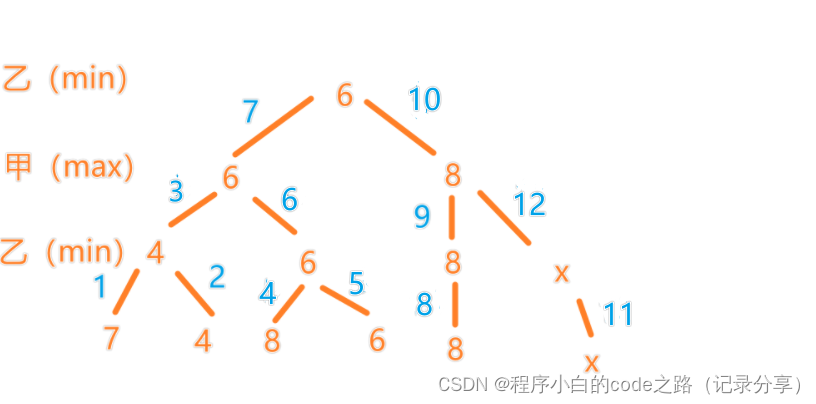
首先,我们可以先来看一下算法导论上给出的图解:
大家可以自己先看一下
然后,我来带大家走一遍这个过程:
其实就按照上面的思想一步步走就行了。
按照上面说的,将所有结点分为两组S和Q,S是已经确定最短路径的结点集合,Q 为其余未确定最短路径的结点集合。
那起始的时候,可以认为S是空的,所有结点都在Q里面。
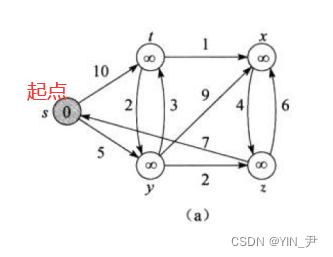
然后这里选择的起点是s
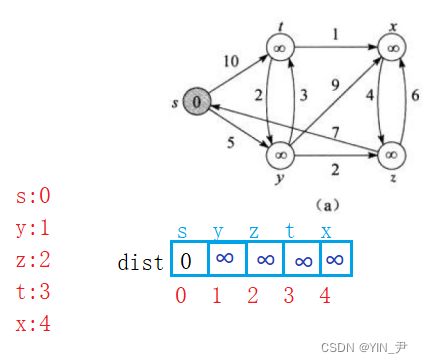
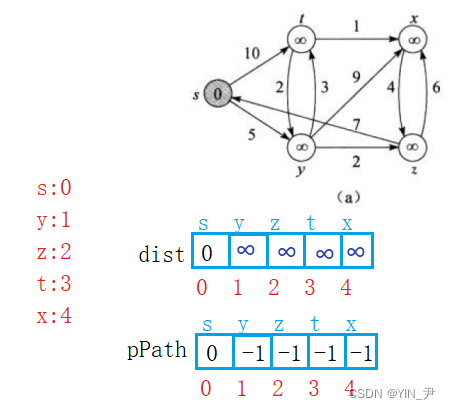
每次从Q 中找出一个从起点到该结点代价最小的结点u,那第一次这个结点u就是s,可以认为s到s的距离是0(图中每个结点里面的值就表示当前从起点到自己的最短路径,还没更新的路径用∞标识),那把s结点放到S集合里面,Q中删去s;
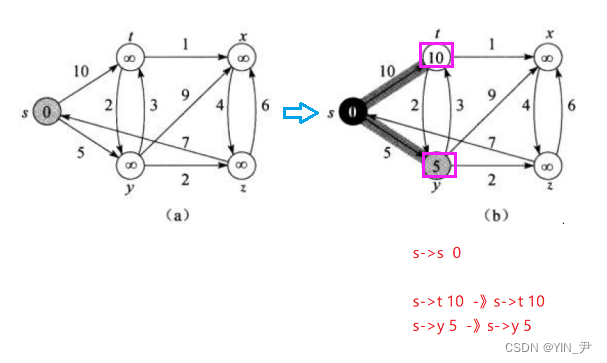
然后对s 的每一个相邻结点v 进行松弛操作(其实去更新起点到它相邻点的距离),s到它相邻的两个结点距离s-t为10,s-y为5,都比原来从起点到它们的距离小,所以更新
然后再从Q里面找一个到起点路径最短的点,那这次找到的是y(此时s-y为5是最小的),把y从Q中移除,放入S里面;
然后对y进行松弛操作
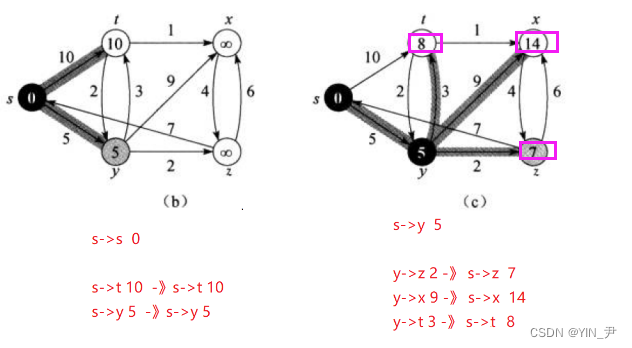
y相邻的几个顶点到y的距离+y到起点s的距离都比之前起点到它们的距离短,所以都更新
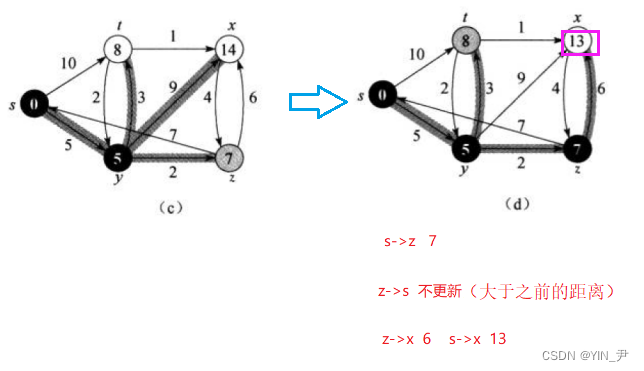
接着继续从Q中选一个到起点距离最短的是z,z从Q中移出,放入S;
接着对x进行松弛操作,更新相应的距离
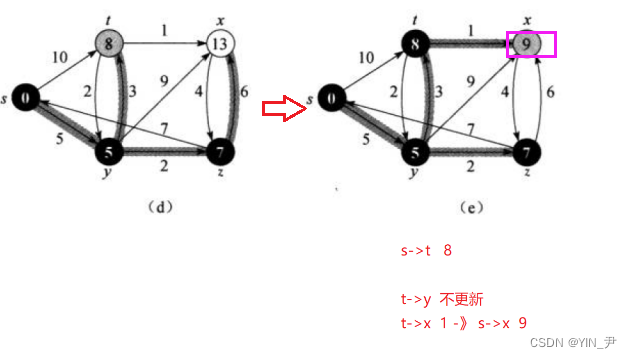
接着继续从Q中选一个到起点距离最短的是t,t从Q中移出,放入S;
接着对t进行松弛操作,更新相应的距离
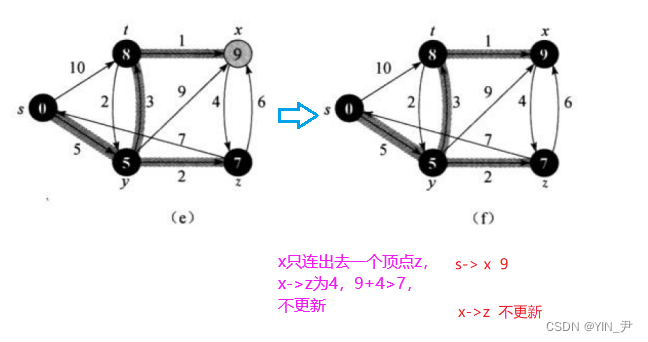
再接着继续从Q中选一个到起点距离最短的是x,x从Q中移出,放入S;
接着再对x进行松弛操作
至此,集合Q 为空(起始Q是满的,所以n个结点的话,其实就选了n次去更新),即所有节点都已经查找过一遍并确定了最短路径
算法执行结束!
如何存储路径及其权值
相信算法现在大家已经理解了,但是还有一些问题需要我们解决:
既然我们是要求最短路径,那肯定得把相关的信息存储起来啊,上面图中直接把每个顶点对应最短路径的权值直接写到了结点里面,而且每条路径是怎么走的,经过了哪些顶点,我们也很容易看出来。
可是后面我们要写代码,那在写代码的时候我们如何把这些信息也存储起来呢?
🆗,是这样处理的:
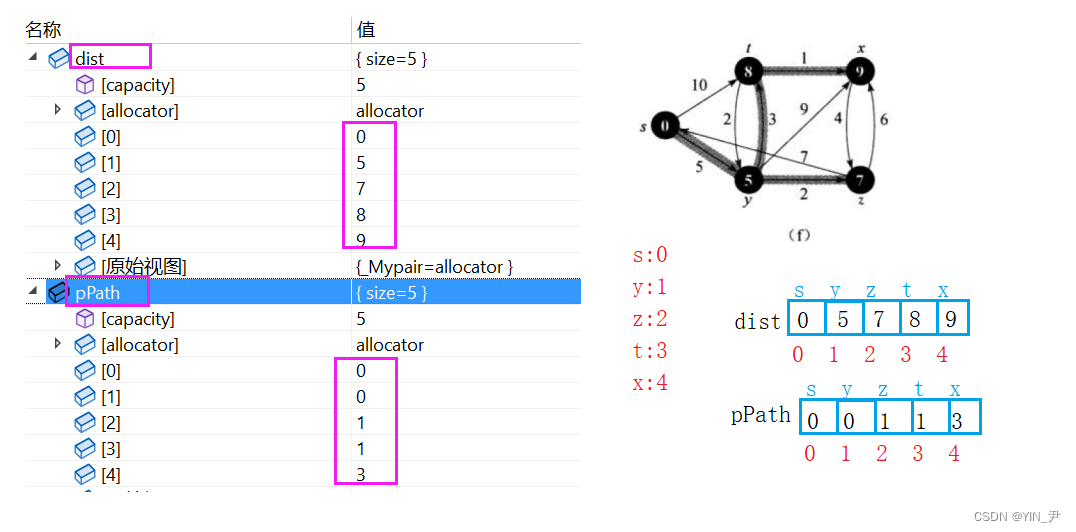
因为每个顶点不是都映射一个下标嘛,所以我们就可以搞一个数组,每个下标映射的顶点是谁,这个位置就存储起点到这个顶点的最短路径。
那最开始就是这样的:
然后后面我们每次更新最短路径的时候修改里面的权值就行了
那上面存的是最短路径的权值,那路径又要如何存储呢?
一条路径可能会经过多个顶点啊。
🆗,那这里呢还是用一个一维数组就可以搞定:
怎么做呢?
很简单,每个顶点映射的位置存储路径上在它前面的那个顶点映射的下标,如果把路径看成一棵树的话,就是存储它的父结点的下标
比如最开始就可以这样存
首先s自己就是起点,可以认为最短路径就是s->s,所以它存自己的下标,然后剩下的顶点都还没有更新最短路径,起始存一个-1
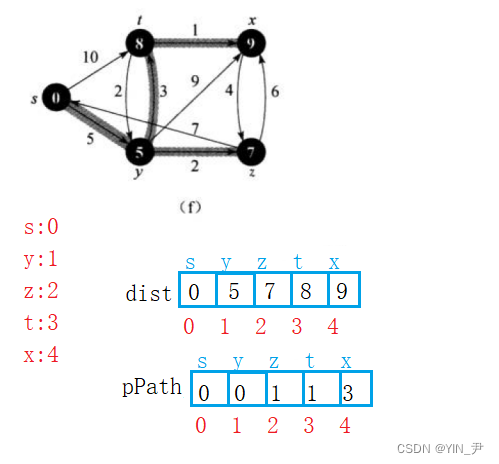
接着每走一步就去更新数组就行了(存路径上它前面的那个结点(可以认为是它的父结点)的下标,类似并查集那里用的双亲表示法存储),那到最后的时候,就是这样的
那这样存储路径的话我们想要获取一个顶点的最短路径的时候,就从这个顶点开始顺序它的父亲(路径中的上一个结点)往上找就行了,找到起点停止,就是一条完整的路径(类似并查集里面的findRoot顺着父结点向上找根)。
代码实现
那下面我们就来实现一下代码:
首先需要给一个起点,然后两个vector存储最短路径及对应的路径权值
然后,按照我们上面分析的思路走就行了
注释写的比较清楚,相信大家应该很容易可以看懂,说一点就是我们现在用的是邻接矩阵结构,所有查找u相邻的结点是去邻接矩阵_matrix里面找,如果下标[u][v]的位置对应的权值不是MAX_W,那它们就相连的,v就是u的一个相邻顶点,然后再判断如果源节点s到结点u 的代价与u 到v 的代价之和(其实就是距离嘛)是否比原来s 到v 的代价更小,若代价比原来小则要将s 到v 的代价更新为s 到u 与u 到v 的代价之和(更新距离)
调式观察
那这就实现好了,我们可以先通过调式观察一下:
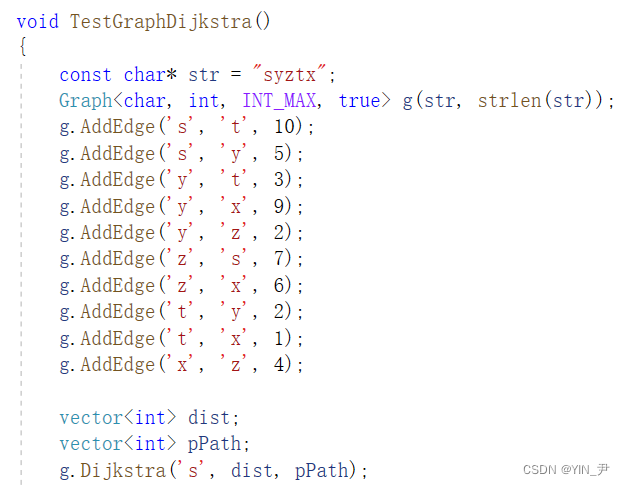
我这里已经写好了一个测试用例(最后会给大家分享源码),这个图就是我们上面讲解思想的时候对应的那个图
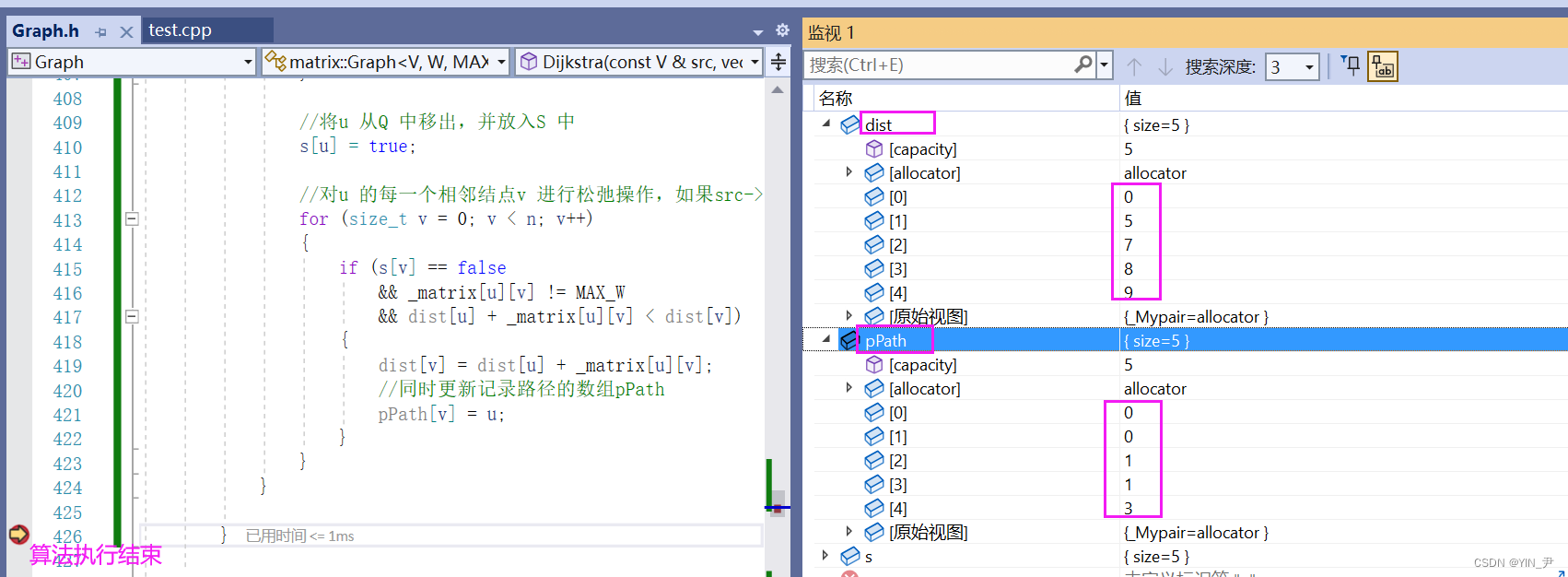
我们来调式观察一下
对比一下我们之前分析的
没有问题,一模一样
打印最短路径
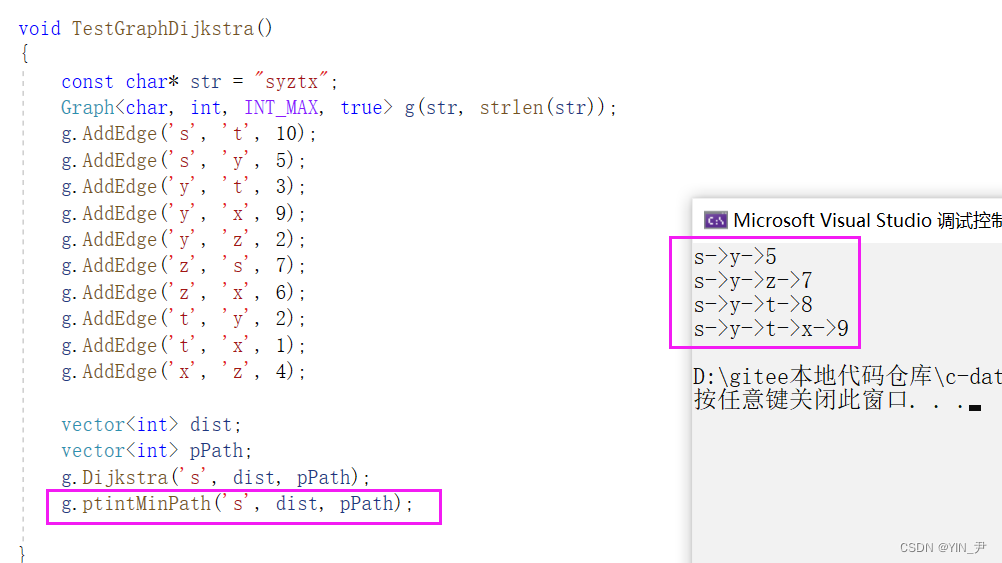
那下面呢我们可以写一个大于路径的函数,把最终得到的起点到各顶点的最短路径以及权值都打印出来看一下,和上面图上的是否一样:
那我们拿到这两个数组就可以去打印
但是这里打印的时候有一个问题:
按我们上面说的,找路径的时候通过pPath数组顺着结点的父亲或者说它的路径上的前一个结点,往上找就行了,找到起点停止。
但是!
这样找出来的路径是不是反的啊,因为我们最后找到的是起点,而正常情况应该是从起点开始嘛。
所以我们要处理一下,也很好搞:
我们可以搞一个vector把路径上的结点保存下来,然后逆置一下,再去打印就行了
来实现一下:
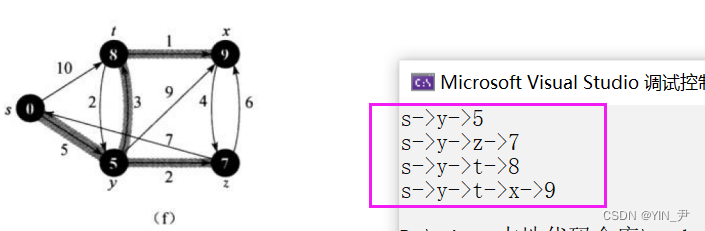
然后我们来打印一下看看:
大家可以对照一下,没有问题
Dijkstra算法的缺陷
但是呢,Dijkstra算法是有一些缺陷的,对于带有负权值的边的图,Dijkstra算法是搞不定的!
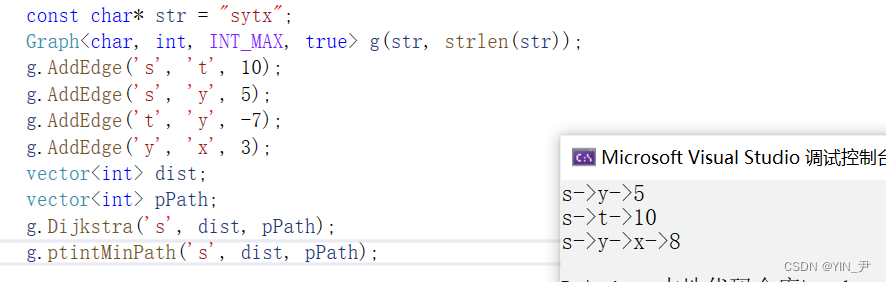
这里呢也准备了一个测试用例,我们可以来看一下:
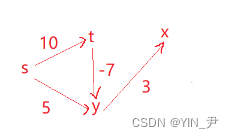
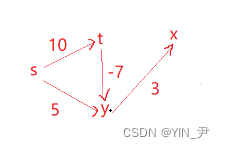
首先它对应的一个图应该是这样的:
那我们现在对这个图执行Dijkstra算法并打印出来看一下:
是这样一个结果
但是我们会发现如果按照这个图有负权值的话,其实有一条最短路径其实没有更新出来,s->t->y应该是3(10+(-7)=3)
也就是说3应该是起点s到y的最短距离,s->t->y是最短路径。
图中带有负权路径时,贪心策略就失效了。
那为什么会这样呢?
因为按照Dijkstra算法的话
这里起点是s,所以第一次选到s,放到S集合里面,然后对s的相邻顶点进行松弛操作,更新距离s->t为10,s-y为5,所以第二次选到y,那y就被放到S集合里面了,而S是已经确定最短路径的结点集合,所以它这里的贪心策略就认为此时的5就是s->y的最短路径距离了(当然如果没有负权值的话这样是肯定正确的),y的最短路径已经确定了。
所以后面再去对t的相邻顶点进行松弛的时候就不会判断st+ty的距离是否小于sy,也不会再更新y的最短路径了,所以上面s->t->y就没有更新出来。因为每次都是从Q里面选的,而y前面已经放到S集合里面了。
但是有了负权值的话,sy的最短路径就不一定是5了(如果全是正的话肯定没问题),后面绕到其它的路径如果遇到负权值就可能会比5还小。
所以对于有负权值的图,Dijkstra算法就不再适用,这种贪心策略就失效了。
那对于有负权值的图我们如何求最短路径呢?
bellman—ford算法可以解决负权图的单源最短路径问题
这个我们下一篇文章就会讲到…
3. 源码
void Dijkstra(const V& src, vector<int>& pPath, vector<W>& dist)
{//初始化一下记录路径和权值(距离)的数组size_t srci = GetVertexIndex(src);size_t n = _vertexs.size();pPath.resize(n, -1);dist.resize(n, MAX_W);//集合S为已确定最短路径的顶点集合,这里我们用一个数组表示S集合就可以//,初始化全false(S中无结点),表示所有顶点都在Q中,//不在S就在Q(其余未确定最短路径的结点集合)vector<bool> s(n, false);pPath[srci] = srci;dist[srci] = 0;//n个结点,需要选择n次去更新路径for (size_t i = 0; i < n; i++){int u = 0;W minDist = MAX_W;//从Q 中找出一个从起点到该结点代价最小的结点ufor (size_t j = 0; j < n; j++){if (s[i] == false && dist[i] < minDist){u = i;minDist = dist[i];}}//将u 从Q 中移出,并放入S 中s[u] = true;//对u 的每一个相邻结点v 进行松弛操作,如果src->u + u->v < src->v ,就更新距离for (size_t v = 0; v < n; v++){if (s[v] == false && _matrix[u][v] != MAX_W && dist[u] + _matrix[u][v] < dist[v]){dist[v] = dist[u] + _matrix[u][v];//同时更新记录路径的数组pPathpPath[v] = u;}}}}void ptintMinPath(const V& src, const vector<int>& pPath, const vector<W>& dist)
{size_t srci = GetVertexIndex(src);size_t n = _vertexs.size();for (size_t i = 0; i < n; i++){if (i != srci)//起点-》起点就没必要打印了{//定义一个vector保存路径上的结点vector<int> path;//从当前结点开始顺着父结点往上走size_t parenti = i;while (parenti != srci){path.push_back(parenti);parenti = pPath[parenti];}path.push_back(srci);//逆置path数组reverse(path.begin(), path.end());//打印路径for (auto e : path){cout << _vertexs[e] << "->";}//打印权值cout << dist[i] << endl;}}
}
void TestGraphDijkstra()
{/*const char* str = "syztx";Graph<char, int, INT_MAX, true> g(str, strlen(str));g.AddEdge('s', 't', 10);g.AddEdge('s', 'y', 5);g.AddEdge('y', 't', 3);g.AddEdge('y', 'x', 9);g.AddEdge('y', 'z', 2);g.AddEdge('z', 's', 7);g.AddEdge('z', 'x', 6);g.AddEdge('t', 'y', 2);g.AddEdge('t', 'x', 1);g.AddEdge('x', 'z', 4);vector<int> dist;vector<int> pPath;g.Dijkstra('s', dist, pPath);g.ptintMinPath('s', dist, pPath);*/// 图中带有负权路径时,贪心策略则失效了。// 测试结果可以看到s->t->y之间的最短路径没更新出来const char* str = "sytx";Graph<char, int, INT_MAX, true> g(str, strlen(str));g.AddEdge('s', 't', 10);g.AddEdge('s', 'y', 5);g.AddEdge('t', 'y', -7);g.AddEdge('y', 'x', 3);vector<int> dist;vector<int> pPath;g.Dijkstra('s', dist, pPath);g.ptintMinPath('s', dist, pPath);
}