一、说明
如果你还没有做过逻辑回归,你会在这里挣扎。我强烈建议在开始之前查看它。您在逻辑回归方面的能力将影响您学习神经网络的难易程度和速度。
二、神经网络简介
神经网络是一个神经元网络。这些神经元是逻辑回归函数,它们被链接在一起形成一个网络,从人脑中获取松散的灵感。在监督式机器学习算法家族中,神经网络及其所有后续架构是一些更难学习、理解和构建的算法。随着这种复杂性的增加,带来了令人难以置信的性能,神经网络能够“几乎”学习任何东西。到目前为止,我们一直将所有的 ML 算法视为函数近似器。我们有数据,但我们想弄清楚定义该数据的函数。神经网络可以近似非常困难和复杂的函数。然而,有时他们是如何做到的似乎令人困惑。事实上,在机器学习中的所有模型中,神经网络可能是最神秘的,通常类似于魔法。
我建议在阅读此博客之前,先观看3blue1brown关于神经网络的系列文章。动画和可视化将帮助您直观地了解神经网络的实际工作原理。
我相信他使用的模型有一些警告,以简化教学。他使用均方误差作为误差函数,使用sigmoid函数作为输出层。我们将继续使用交叉熵误差和softmax激活。我也会避免观看该系列的最后一个视频,因为当您回到这里时可能会导致混乱,因为推导和变量不会相同。
三、设置模型
简单神经网络的架构与我们的 Softmax 回归算法并没有什么不同,我们在之前的博客中已经介绍过。我们只是在神经元输出层之前添加另一层神经元,计算属于每个类的概率。这称为隐藏层,用 z 表示。
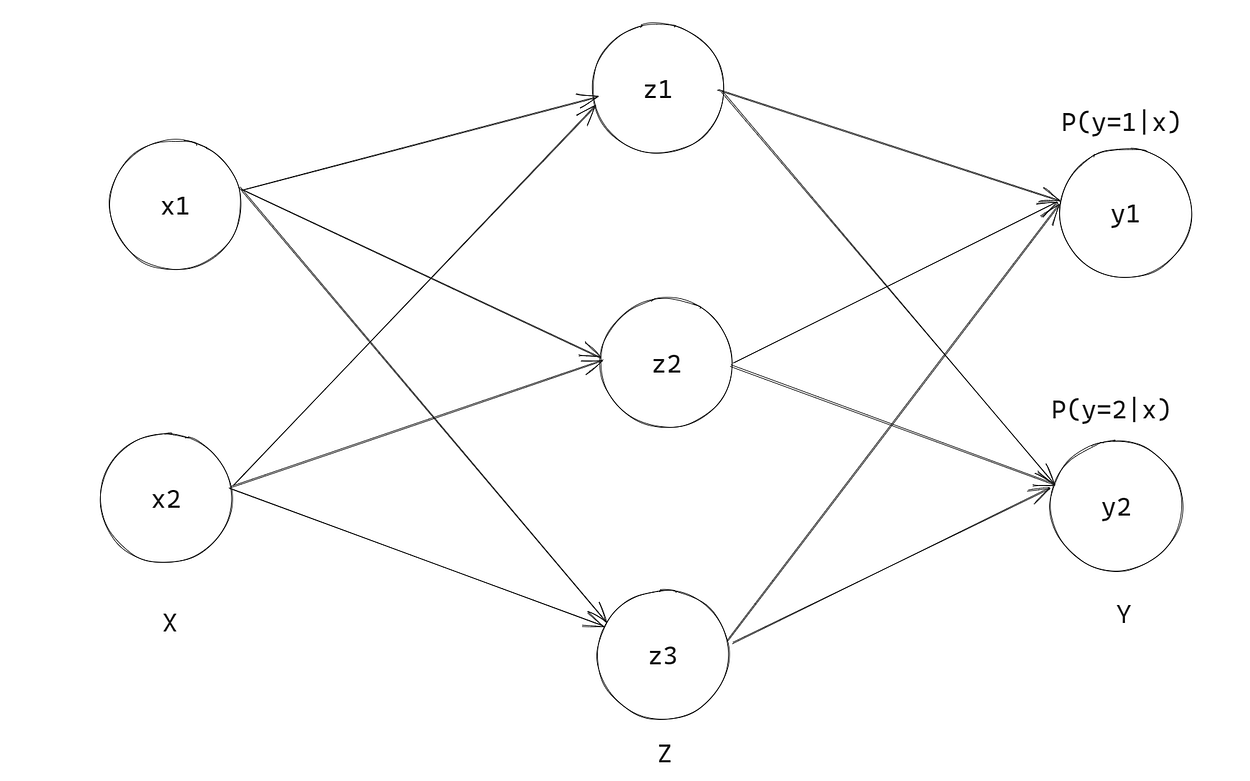
我们现在将坚持只有 1 个隐藏层和 3 个神经元,以保持一切简单。但是,您可以根据需要在每层中拥有任意数量的隐藏层和任意数量的神经元,没有限制。
四、变量名称、符号和表示法
在我们深入研究神经网络之前,拥有某种标准化符号非常重要,这样就不会混淆任何变量的含义。一旦我们开始进行反向传播,这是解决神经网络权重的算法,就会有一堆变量的海啸,让你不知所措。事实上,这可能是反向传播最难的部分,数学与 Softmax 回归相同,只是有更多的变量和复杂性层使其很难跟上。您将希望对符号感到非常熟悉,否则您将在反向传播过程中遇到困难。
- N = 样本
数 - 测量 10 个个体的重量,N = 10 - D = 每个样本
的特征数 - 测量身高、体重和年龄以预测血压。D=3 - X = 大小为 NxD
的数据矩阵 - 每行都是一个样本,而每一列都是该样本的一个特征 - x = 大小为 Dx1 的单个样本
- yn = 来自大小为 Kx1 的第 n 个样本的模型的单个目标标签或预测
- Y = 模型中的所有目标标签或预测作为大小为 NxK 的向量(如果一个热编码)和大小为 Nx1 的矩阵(如果不是)
- tn = 第 n 个样本中的单个目标标签
- T = 所有目标标签作为大小为 NxK 的向量(如果一个热编码)和大小为 Nx1 的矩阵(如果不是)
- P(y=k|x) = 单个值,我们的模型将类 k 预测为概率
- P(Y|X) = 我们对所有 N 个目标的所有预测的矩阵,给定 X,大小与 Y 相同。
- E 或 J = 误差函数 = 成本函数 = 目标函数
现在,我们对 Y 有两种不同含义的原因有两个。使用 Y 表示目标,使用 P(Y|X)对于预测很有用,因为它代表概率,这就是我们想要解释模型的方式。将 T 用于目标,将 Y 用于预测对于推导和编码很有用,因为它使编写方程和代码变得更加简单。我们不想写 P(Y|X)一直以来,它都非常麻烦。
通常,大写字母是指矩阵,而小写字母是指向量/标量。我们将使用小写字母来索引一系列值。例如,我们使用小写的“n”来索引所有 N 个样本。
现在让我们看一下与隐藏层相关的变量,当我们添加更多隐藏层时,我们最终会用完字母来识别它们,因此我们将使用上标。这将使推导在短期内更加混乱,即使我们确实可以访问字母,但最好现在就习惯它们,在神经网络变大之前。否则,一旦从字母的过渡变得不可避免,你就会迷失在所有的方程式中。
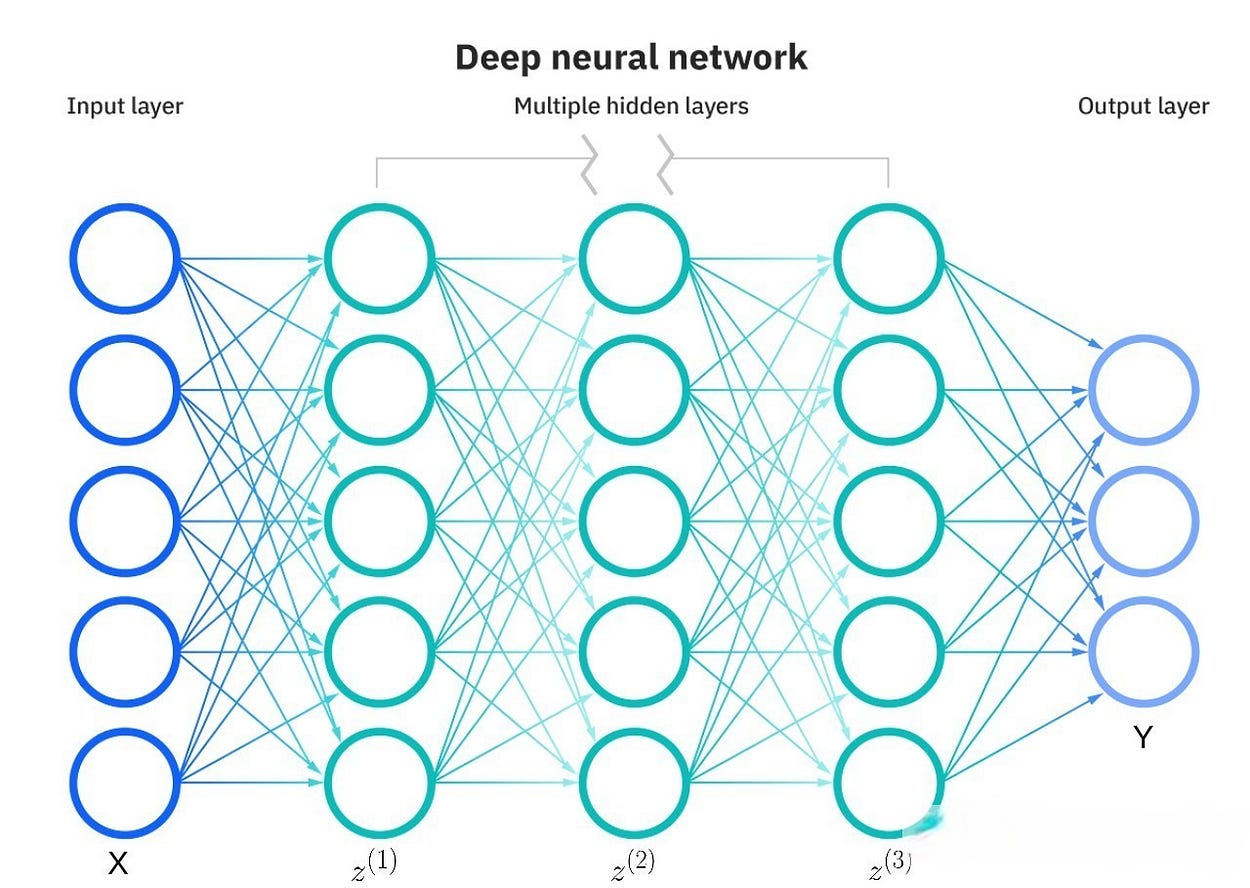
每个隐藏层都有自己的一组权重和偏差,我们将使用上标来引用每个相应的变量。
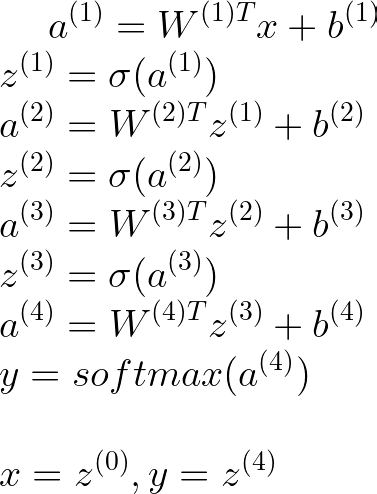
我们还引入一些变量来计算隐藏层及其各自的神经元
![]()
我们还希望能够为不同形状和大小的神经网络执行此操作,而不仅仅是我们上面计算的神经网络。我们将把信仰的飞跃从这个具体的例子带到一个抽象的、广义的前向传播的表示。
让我们创建一个更通用的权重矩阵版本,可用于任何隐藏层。
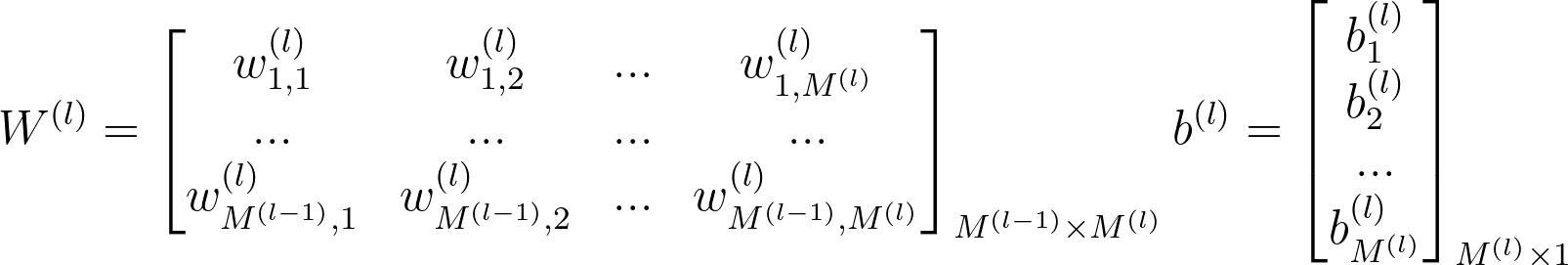
注意矩阵的大小,任何给定隐藏层的权重矩阵 W(l) 的大小取决于前一层的大小。
有2种特殊情况,上述尺寸不适用,连接到第一个隐藏层的输入层的权重矩阵,以及连接到输出层的最后一个隐藏层的权重矩阵。让我们也来看看这些。
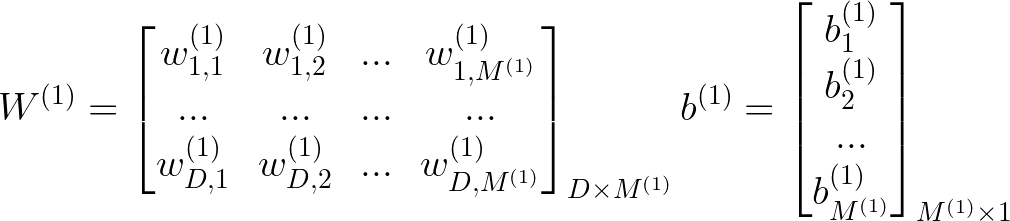
我们可以想到 D=M(0)
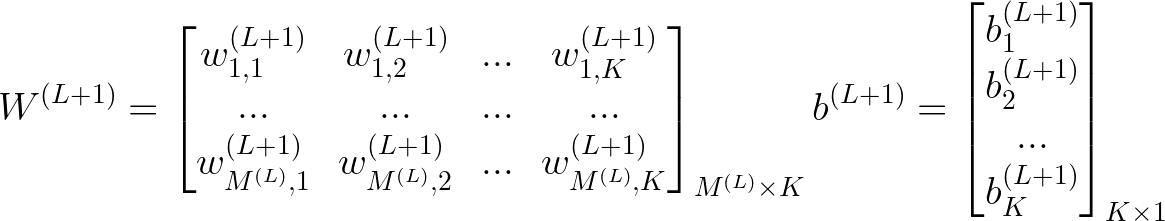
我们可以想到 K=M(L+1)
现在,我们可以很容易地引用任何大小的神经网络的权重矩阵,在任何给定层上都有任意数量的神经元。
五、前向传播
5.1 一般理解
我们可以很容易地创建一个小型神经网络,并使用随机权重进行预测。这称为前向传播。让我们继续之前的示例,其中包含 2 个输入节点、一个包含 3 个神经元的隐藏层和 2 个输出节点。所以在这种情况下,L = 1 和 m(1) = 3
让我们首先为我们的小型神经网络分配一些随机权重,并初始化输入和输出。
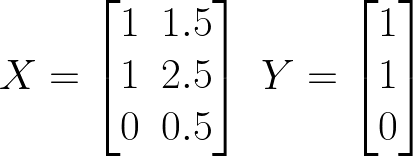
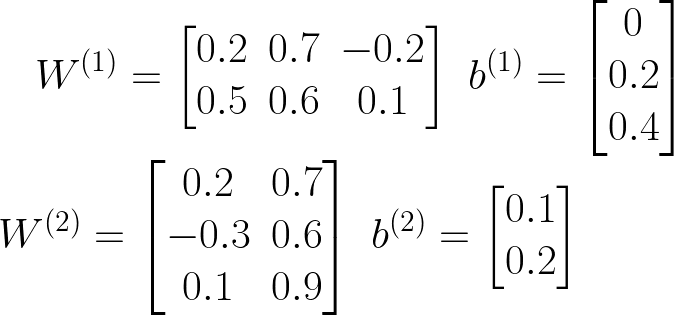
让我们一起做一个 1 个样本预测,从 X 的第一个样本开始。首先从输入层到隐藏层。
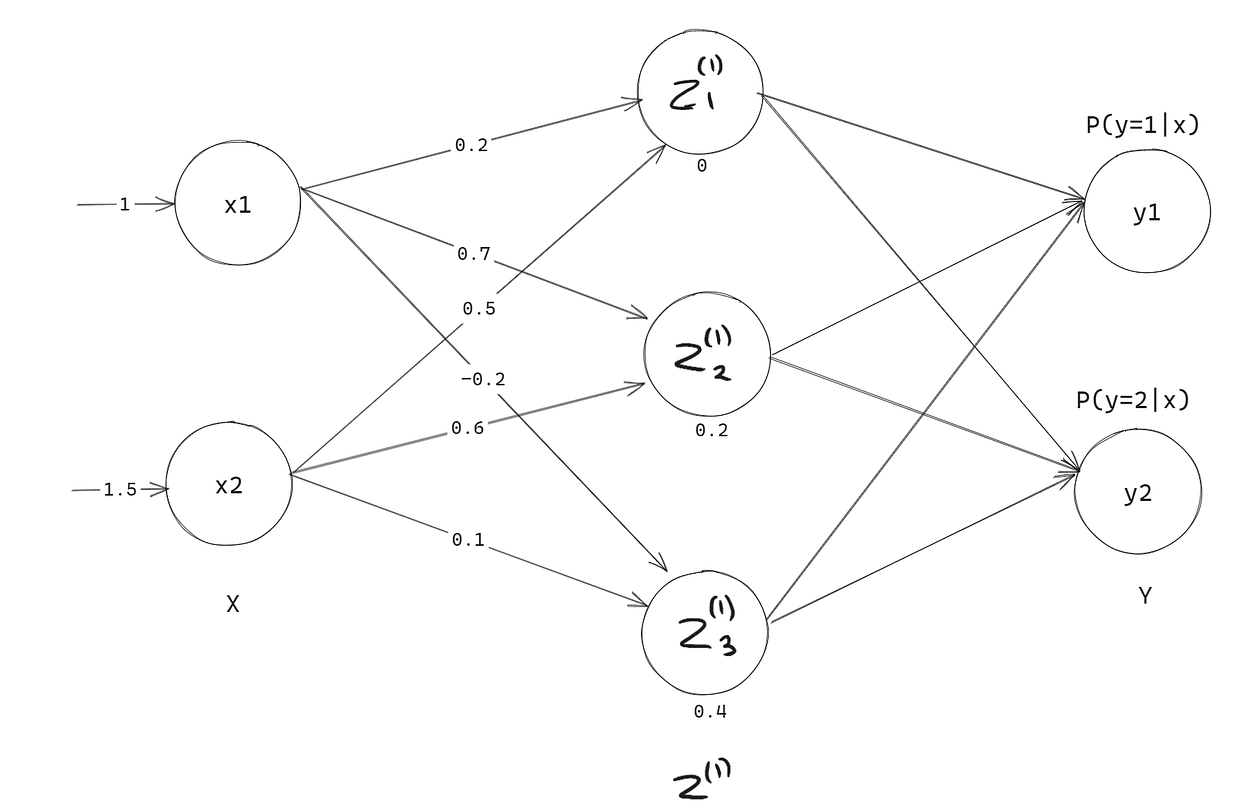
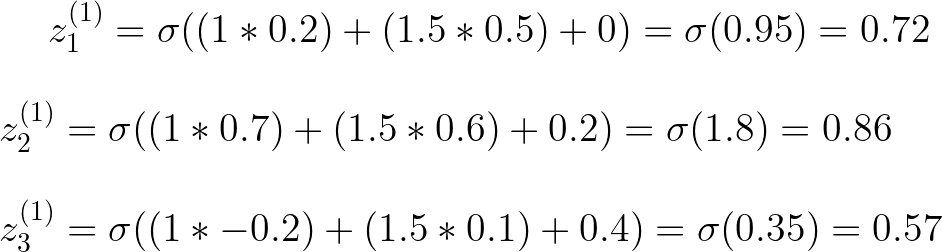
现在从隐藏层到输出层。


让我们回想一下softmax公式

概率总和为 1 !
如果您想要更多练习,我建议您手动浏览 X 中的其他 2 个样本并计算结果。
5.2 矢量化模型
现在,手动逐个执行所有这些计算非常慢,我们还希望能够在代码中表示前向传播。我们希望能够立即计算所有 N 个样本的预测。我们已经熟悉了前面博客中的复合函数和矢量化,所以让我们在这里应用它。
对于单个样本,我们有
![]()
对于所有 N 个样品,我们有
![]()
关于偏差项的大小,这里实际上存在一个数学错误。让我们快速浏览一下。
让我们回想一下 X、W 和 b 的大小

请记住,矩阵加法要求矩阵的大小相等,因此实际上 b 的大小必须如下所示为 NxM(1) 才能在数学上正确
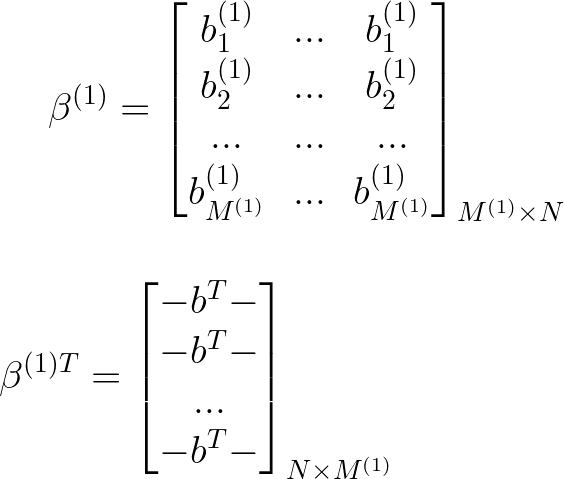
基本上,这样做是确保为所有N个输入添加偏置项。
幸运的是,当我们编码时,NumPy已经在我们编写时自动为我们执行此操作
X.dot(W) + b 我们拥有构建第一个前馈神经网络所需的一切对模型进行编码
六、反向传播
在我们深入研究深度神经网络的梯度之前。让我们继续我们的 1 个隐藏层的例子,并从那里慢慢建立起来。我想明确指出,更重要的是了解我们为什么以及如何进行反向传播,而不是担心微积分。微积分只是一个机械计算,在实践中,当我们使用TensorFlow和PyTorch等深度神经网络库时,它们会自动为我们完成所有微积分并找到梯度。因此,如果您不能立即进行推导,请不要气馁,这并不意味着您不擅长机器学习,只是意味着您需要复习微积分。您仍然可以继续并在代码中实现模型。
我们的损失函数与 Softmax 回归相同。但是现在我们有 2 组权重需要解决,而不仅仅是 1 组。我们从网络最末端的权重开始,因此称为“反向传播”,因为将这些权重更改一些小值(导数)只会导致输出层发生变化。随着我们在网络中的进一步,权重的一些微小变化将影响网络中后续隐藏层的权重。
让我们像往常一样快速可视化我们希望采用的导数,如果我们对 W(2) 中的单个权重进行一些小的更改,其他变量将受到影响,这就是链式规则的关键。
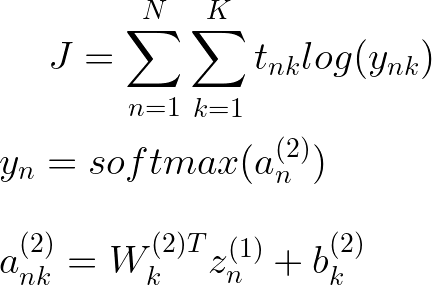
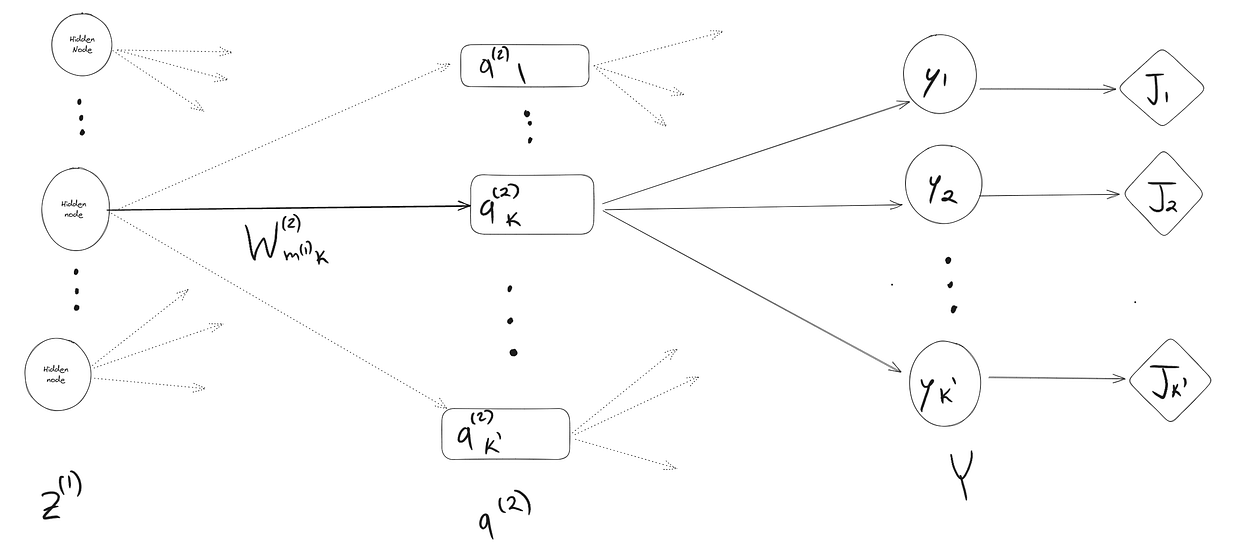
召回 k' 是一个虚拟变量,用于索引 K
总的来说,我们得到了这个导数,它几乎与softmax导数相同,只是变量命名约定有点不同
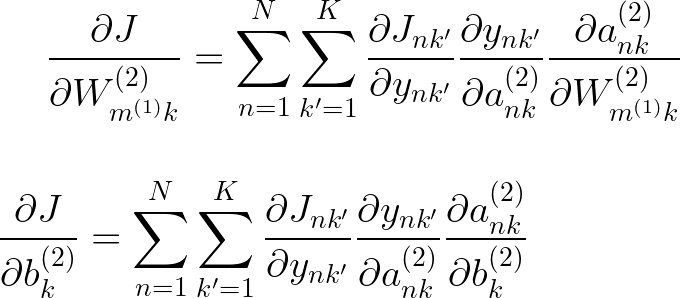
方便的是,当我们进行softmax回归时,我们已经计算了这两个方程的前两个导数,而第三个导数类似于softmax回归中的导数,其中它只是线性项的导数。

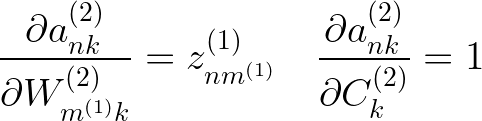
把所有的东西放在一起,我们得到
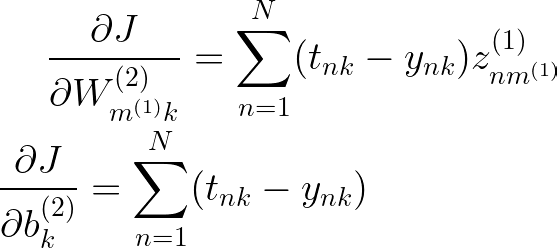
到目前为止还不错,现在我们需要取下一组将输入层连接到隐藏层的权重和偏差的导数。
现在,如果我们对 W(1) 中的权重进行一些小的更改,这将对所有后续变量产生蝴蝶效应。让我们快速可视化一下。
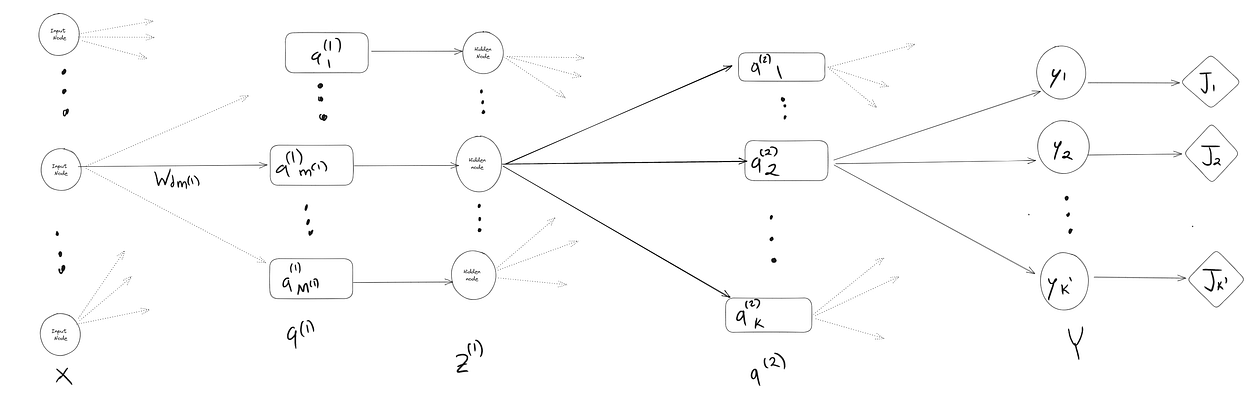
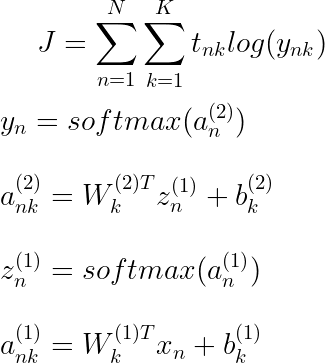
由于 K 不再出现在外部项中,我们必须对 K 求和以获得我们的偏导数。直觉上这是有道理的,因为现在我们对 W(1) 中的权重所做的任何小更改都会影响权重连接到的神经元,这将改变所有 k 激活,然后会影响所有 k' softmax 函数。k 和 k' 的总和都在 K 之上。
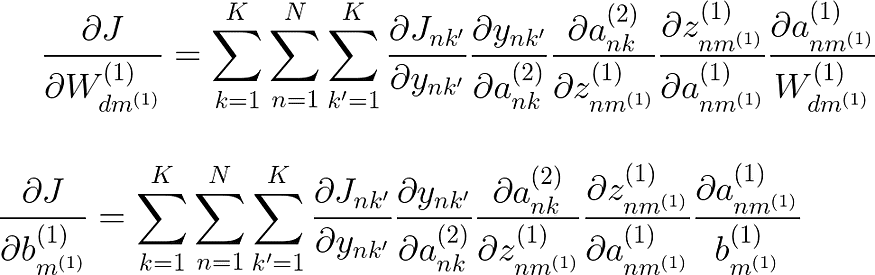
在重用它们(传播)之前,我们已经计算了其中一些导数。

以下衍生品也非常简单。
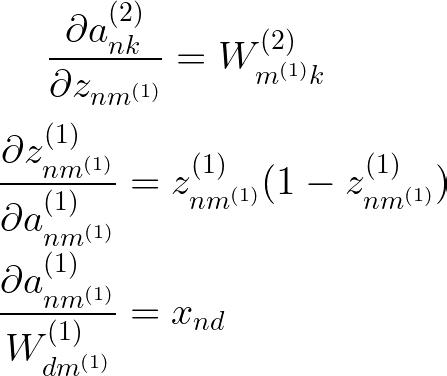
我们可以使用激活本身来表示 Z(1) 层激活函数的导数。我们在进行逻辑回归时已经计算了这个导数。假设我们想使用不同的激活函数,我们可以替换
现在把所有东西放在一起
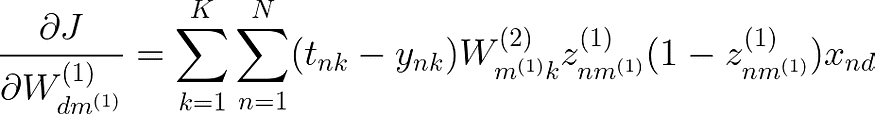
最后一步是对此进行矢量化,以使计算快速简便。让我们看一下这些矩阵的大小,如果我们扩展 2 个总和、所有权重和所有输入。
![]()
我们想操纵这个术语,以便所有的乘法在维度方面都是有效的。我们先来看看 W(2) 的转置
![]()
现在我们可以定义激活函数梯度 Z(1-Z) 与 T-Y 和 W 转置之间的乘积之间的元素乘法。
![]()
最后取 X 的转置,我们有一个完整的方程来表示 W(1) 中所有权重的梯度。
![]()
生成的矩阵应为 DxM(1),其大小与 W(1) 相同,后者表示 W(1) 中所有权重的梯度。
七、 添加更多图层
现在,如果我们想添加第二个隐藏层,甚至更多,导数将变得相当长且计算繁琐。幸运的是,像PyTorch和TensorFlow这样的深度学习库中存在自动差分,我们在编程时不必担心这一点,但理解理论仍然很重要。您可能已经注意到,此导数存在一种反复出现的模式,我们可以重用我们之前计算的导数,并且随着我们添加更多层,无论大小如何,导数的整体结构都保持不变。我们可以利用这一点为任意数量的隐藏层编写更通用的解决方案。
让我们将之前的神经网络扩展到两个隐藏层,而不仅仅是一个。

我们已经解决了 W(3) 的导数。

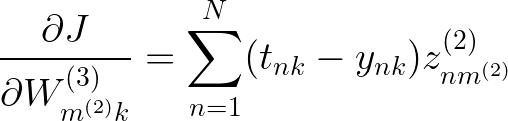
W(2) 的导数也应该类似于我们之前求解的导数。唯一改变的是变量命名和最后一个偏导数,因为 W(2) 依赖于前一个隐藏层 Z(1),而不是像以前那样依赖于 X。
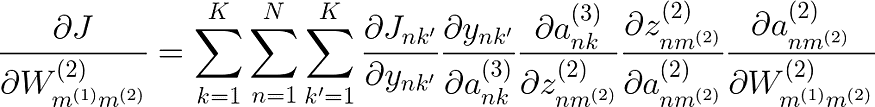
尝试像我们之前那样绘制神经网络来仔细检查这个导数。
解决方案是

现在终于到了 W(1) 的导数。这个导数会很长,但我希望你尝试自己找出模式并慢慢计算导数。
![]()
你会注意到,我们已经解决了所有这些衍生物,只是上标不同,现在也许能够理解为什么我说我们从一开始就使用上标更好。
为了推广,假设我们想使用不同的激活函数,我们可以将激活函数的导数替换为 z',而不是像我们现在这样将 sigmoid 的导数替换为 sigmoid,那么您可以简单地将 z' 替换为所选激活函数的重复导数。
最后我们得到
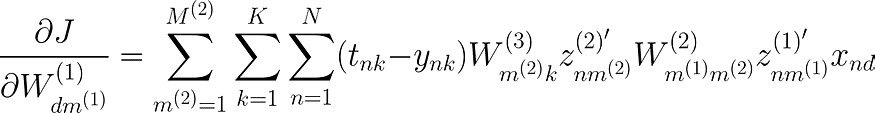
八、确定模式
您可能已经注意到,当我们添加新的隐藏层时,我们正在添加 2 个新项,因此我们的第一层梯度有 7 个导数,第二层有 5 个导数,第三层有 3 个导数。

我们越往前走,我们遇到的术语就越常见
每次创建新层时,我们都会添加一个线性变换和一个激活函数。
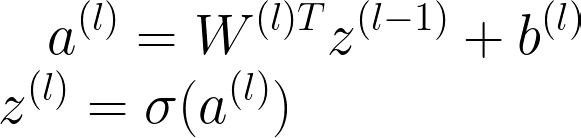
进行中.....拉曼欣德





![[开源]MIT开源协议,基于Vue3.x可视化拖拽编辑,页面生成工具](https://img-blog.csdnimg.cn/img_convert/b55fb4e85a01ec6e03aa764f5a511797.png)