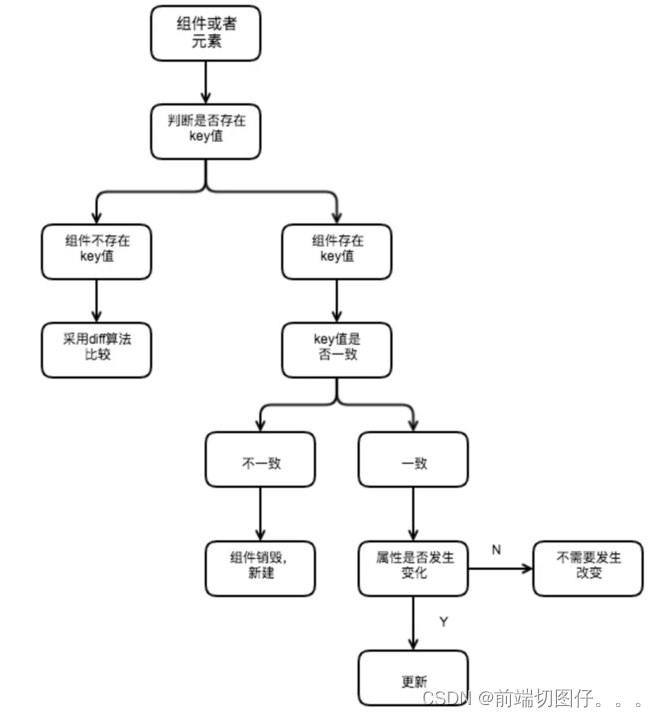
Metric Tensor--度量张量
度量张量可以测量空间的长度和角度。
How do you get the length of a vector ?
(正交基的话)可以使用三角形的勾股定理(毕达哥拉斯定理)。
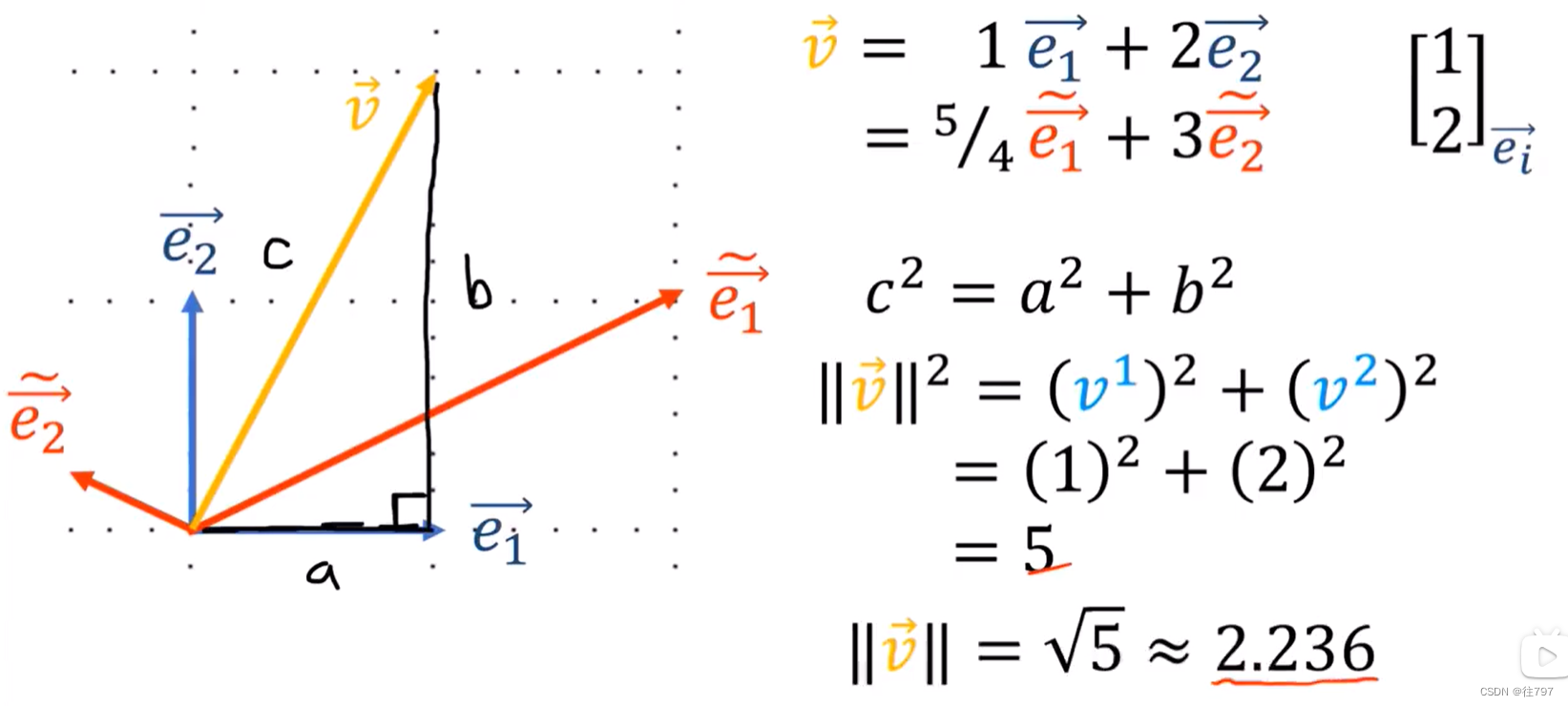
上面用的是正交基e1、e2来计算的, 但是,若你想用 利用勾股定理计算就行不通,因为
和
不是正交基,无法这么计算。
Pythagoras's Theorem is a lie for non-orthonormal bases.毕达哥拉斯定理对于非正交基而言是个谎言。 其仅在基底向量长度为1且正交的情况下成立。
事实上,若我们使用不同的坐标系,其中一个向量V总是平行于一个基向量时,毕达哥拉斯定理就不起作用。
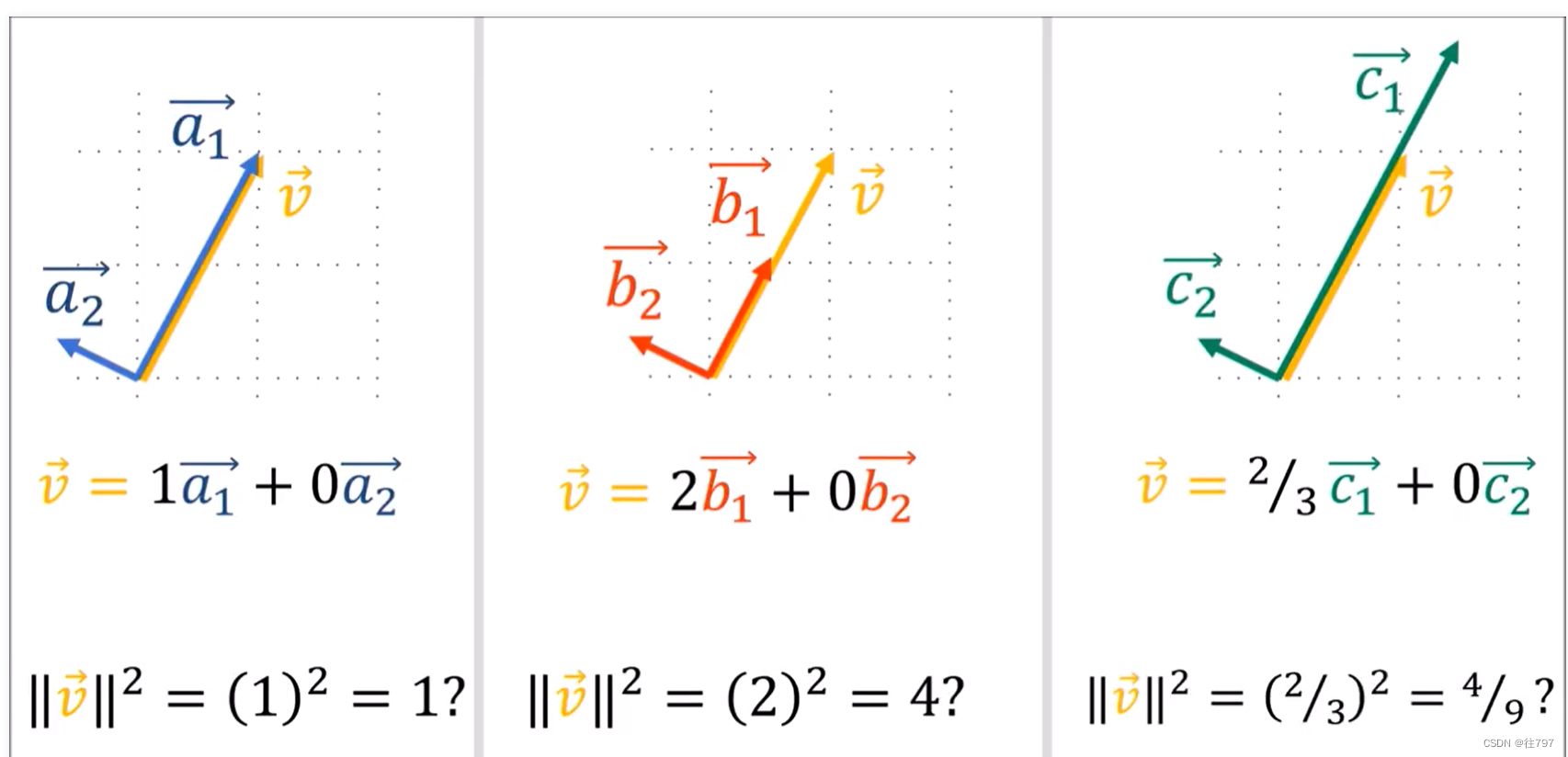
从这三个例子可以看出,对于一般的非正交坐标系,毕达哥拉斯定理对我们没什么好处。
事实证明,向量长度的真正公式不是由毕达哥拉斯给出的,而是由点积给出的,。
所以向量V的平方长度 = V · V、
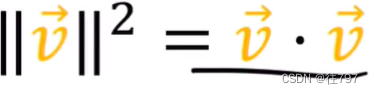
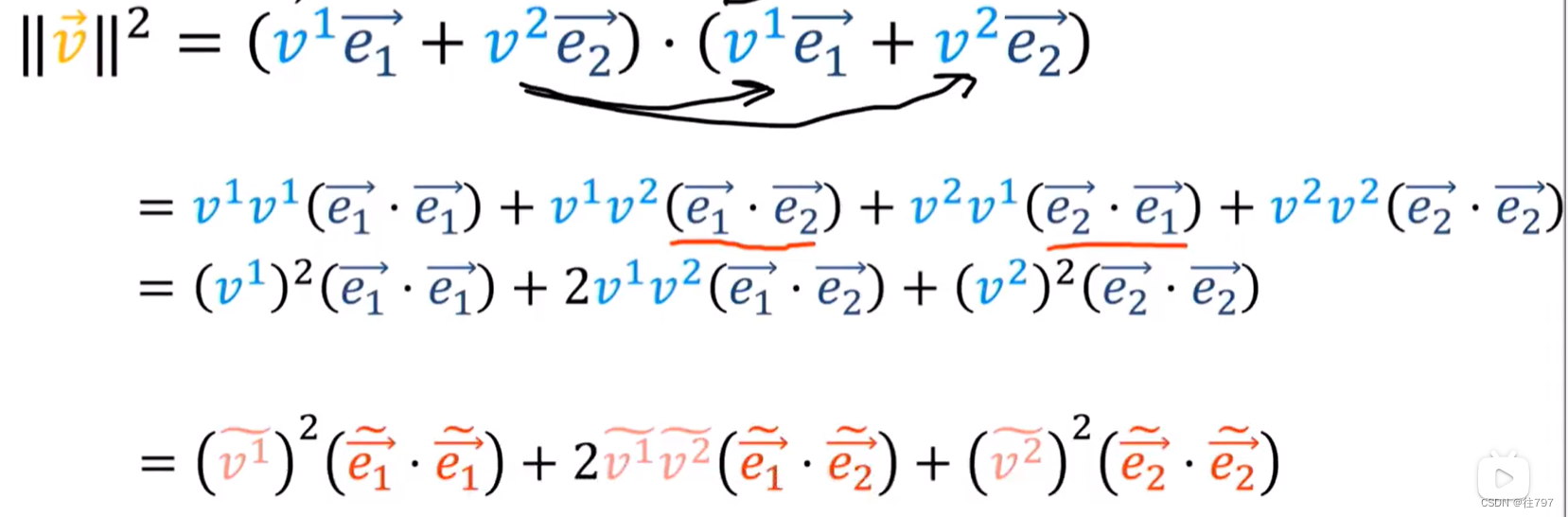
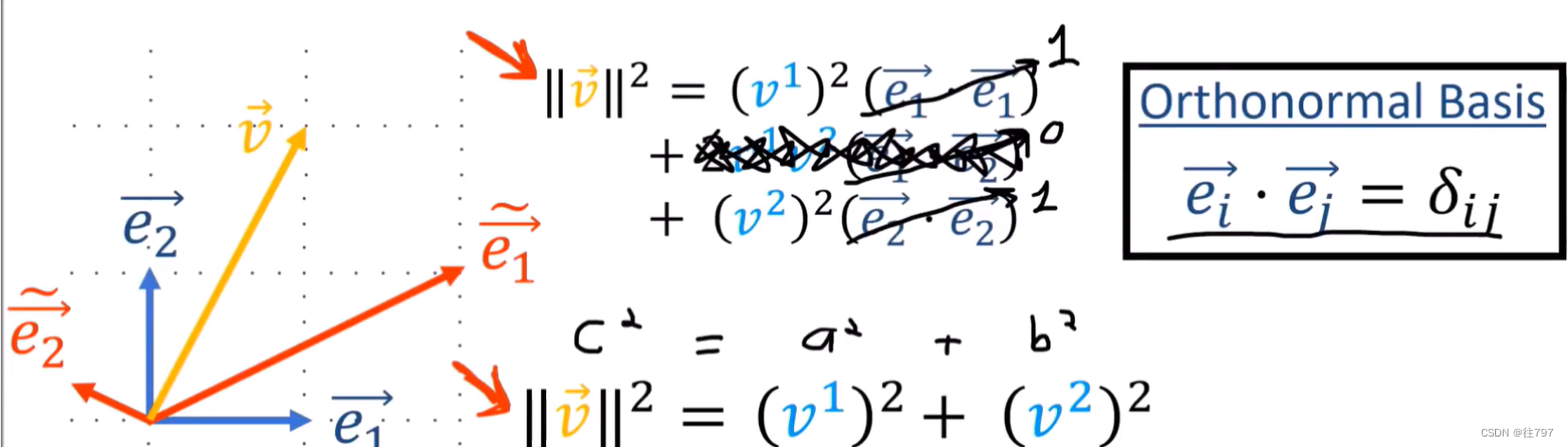
orthonormal basis -----正交基
上面第一个红色箭头的就是 向量长度的真正公式;
而下面第二个红色箭头是因为正交基,才有这么简单的公式出来。
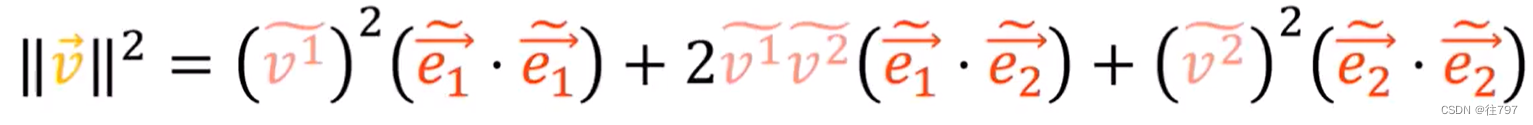
而在这个新基的基底下,就不会有那么简单的式子了,因为和
不是正交基 , 长度也不为1。
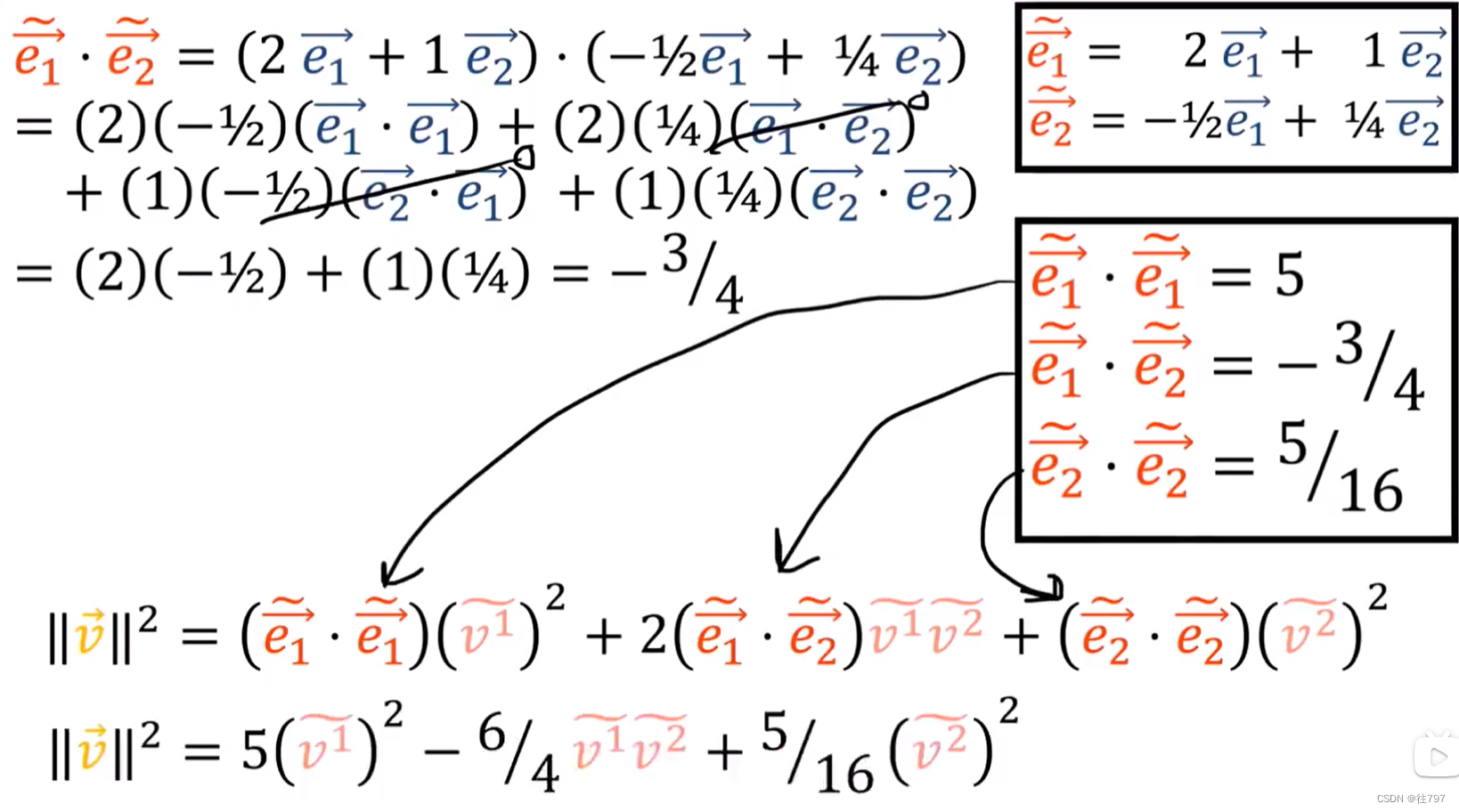
但是另有办法计算, 也就是想办法计算出 、
、
,
而要怎么计算这个呢? 我们知道e1 · e1 =1 , e1 · e2=0 , e2 · e2 = 1.
故可将新基用旧基来线性表示,再展开计算。
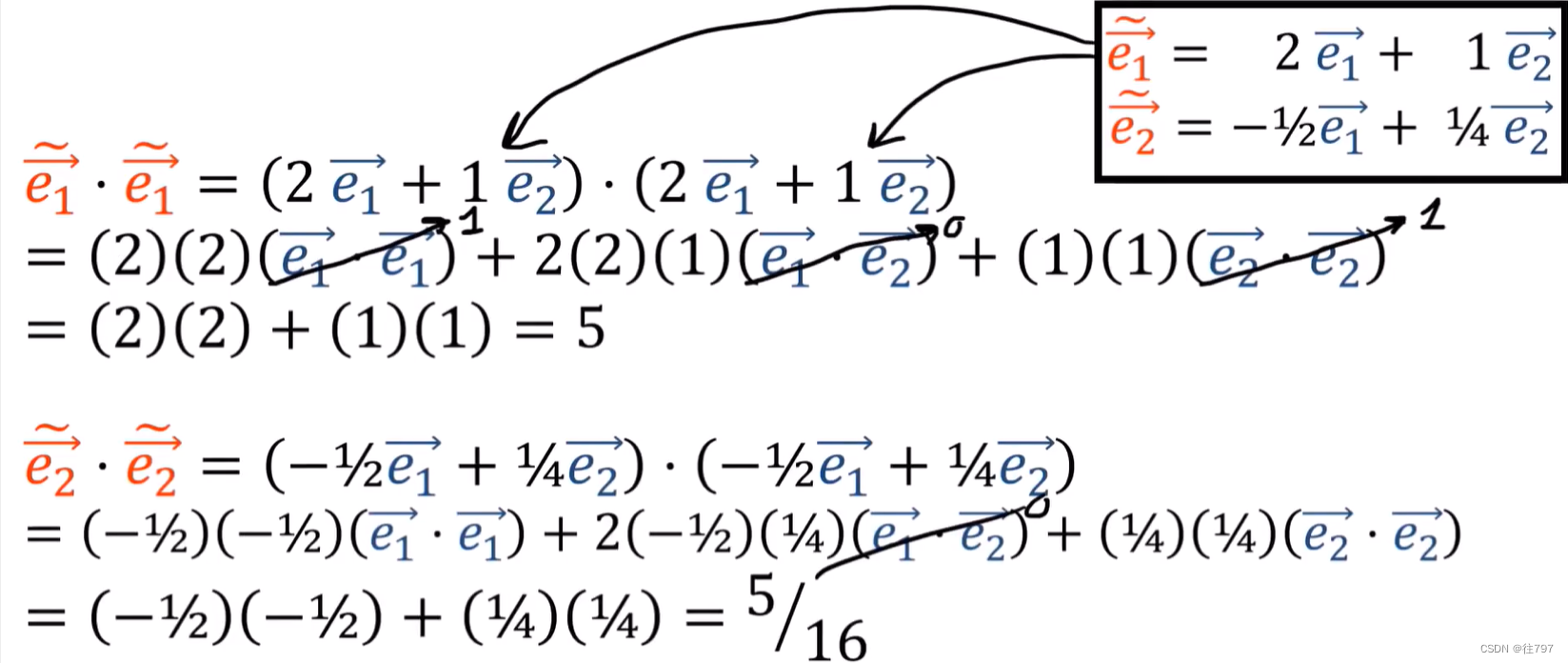
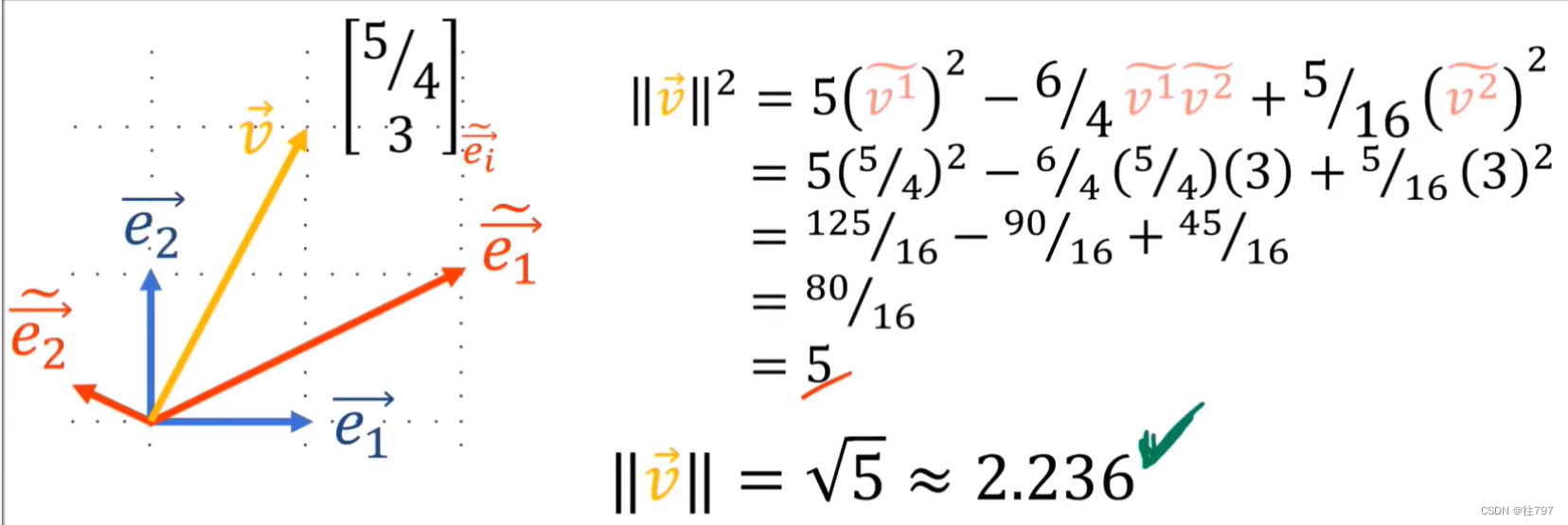
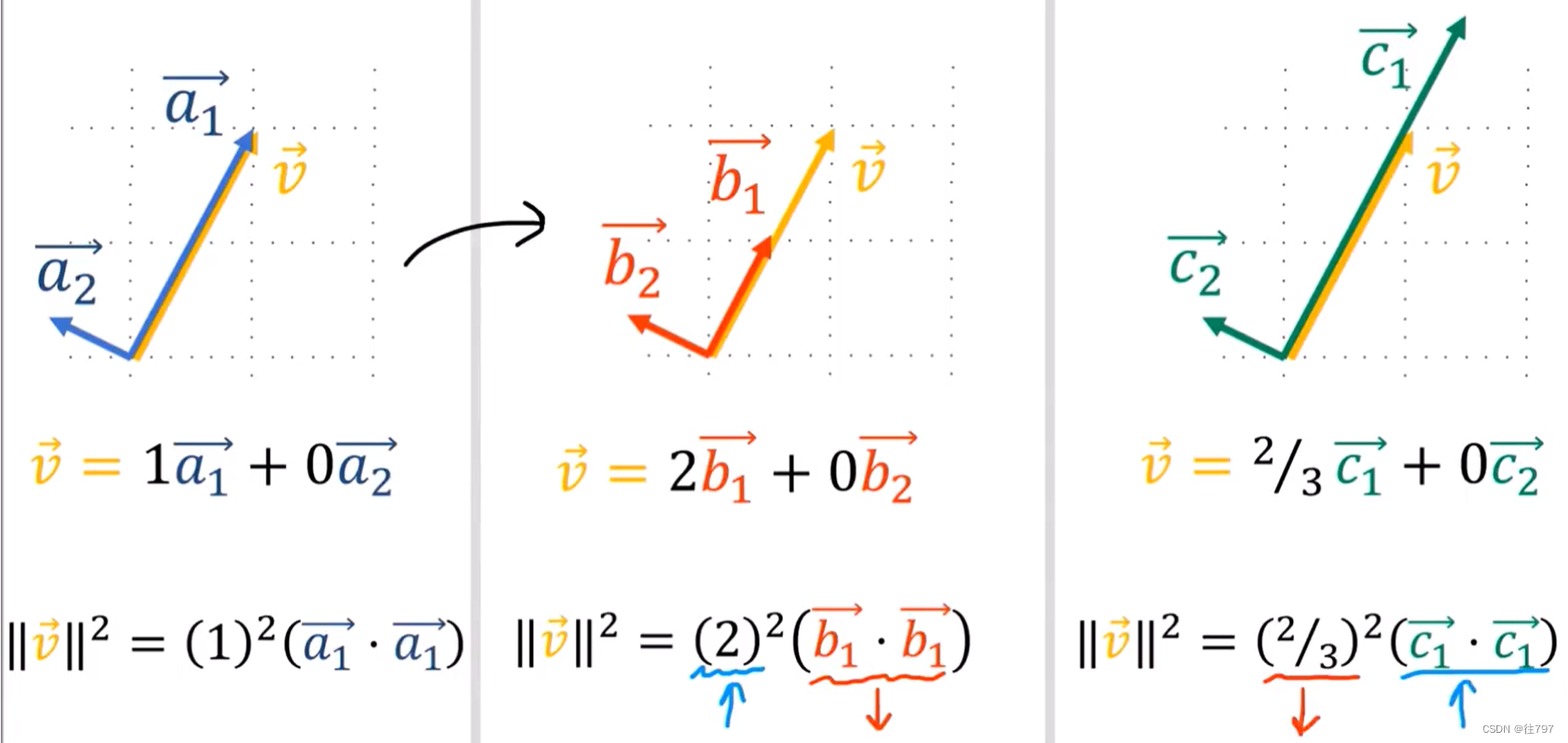
这新公式通常有效,原因是放向量的分量变大时,基向量会变小,因此,当从“a“变到”b“时,
比较左、中图,发现向量的组件从”1“变大为”2“,与a1相比,b1会缩小。
因此,分量的增长和基向量的点积的缩小将平衡,长度将相同。
类似的,中、右图比较,分量缩小,则基向量的点积将增大以平衡事物,并且长度将保持不变。
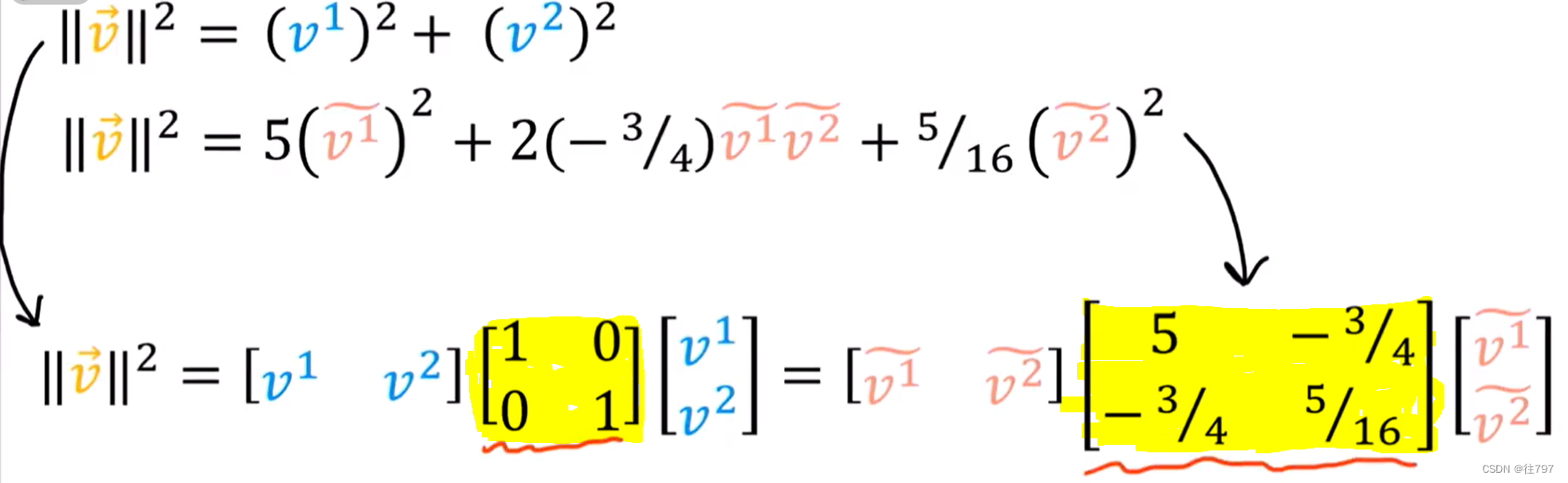
看图,我们可以把向量的长度写成矩阵的乘法形式,
在任何给定坐标系中获取向量长度的关键是 这里的矩阵。
这就是我们所说的度量张量。
用字母g来表示度量张量,
看下图,左边这个是旧基中的度量张量,右边这个是新基中的度量张量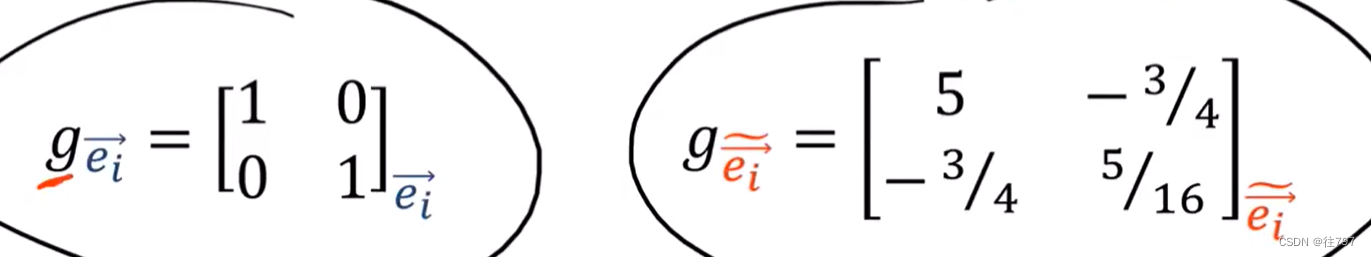
它们度量的是同一个向量V的长度,也就是说,它们是相同的度量张量,它只是由不同的矩阵表示,就像向量一样,度量张量是不变的,但是,当使用不同的坐标系时,它们看起来不同并且具有不同的组件。
因此,归根到底,要使用下图这些公式来获得向量长度,只需要知道基向量点积,
我们可以将e1 · e1 , e1 · e2, e2 · e2 这些乘积存储到一个矩阵中,该矩阵表示该坐标系的度量张量。 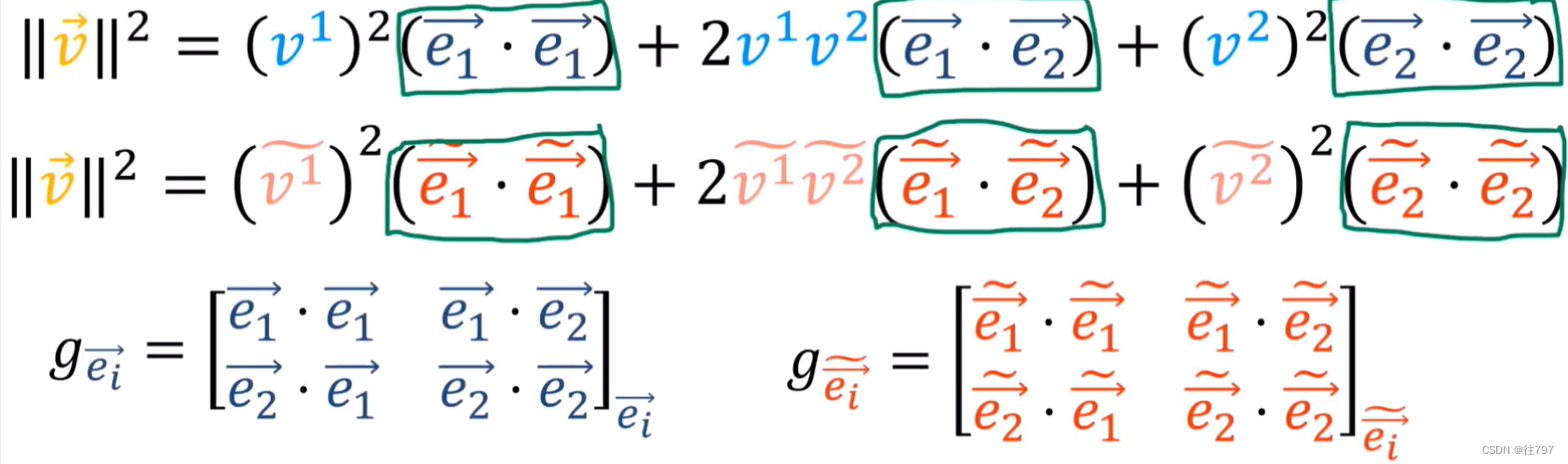
因此,要获 得 向量长度 的平方,可在这里使用下面这些简单的公式,
注意,这里有隐含对 i 和 j 的求和,度量张量的分量由基向量的点积给出。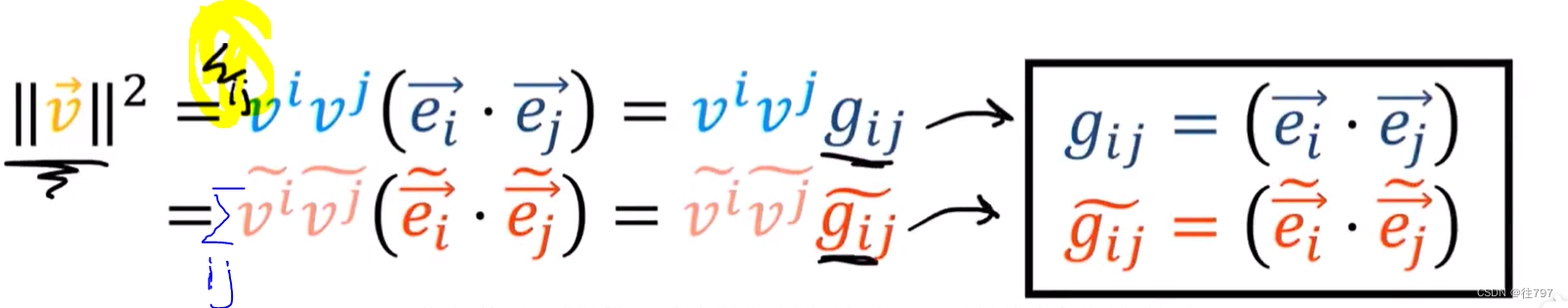
以上就展示了如何利用度量张量来计算向量的长度。
接下来展示 如何利用 度量张量来测量角度。
有以下坐标系:
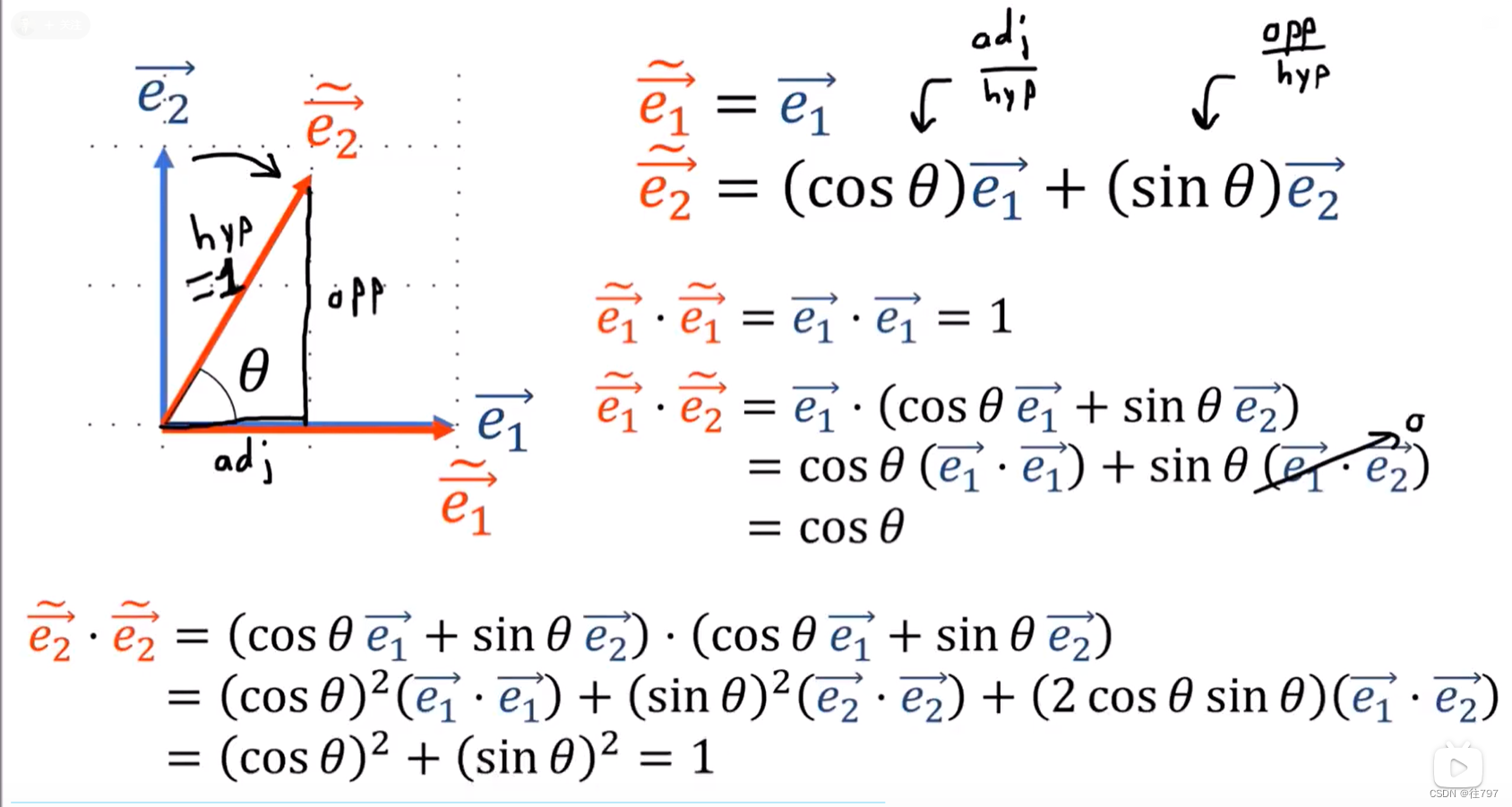
故有:
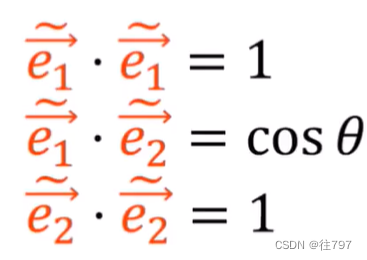
还有度量张量如下:(注意:这两个是同一个度量张量,只是在不同的坐标系下,有不同的分量而已,)
假设有两个向量V 、W, 想测量它们之间的角度。
和
与向量V 、W 的方向相同,且
和
的长度都为1。
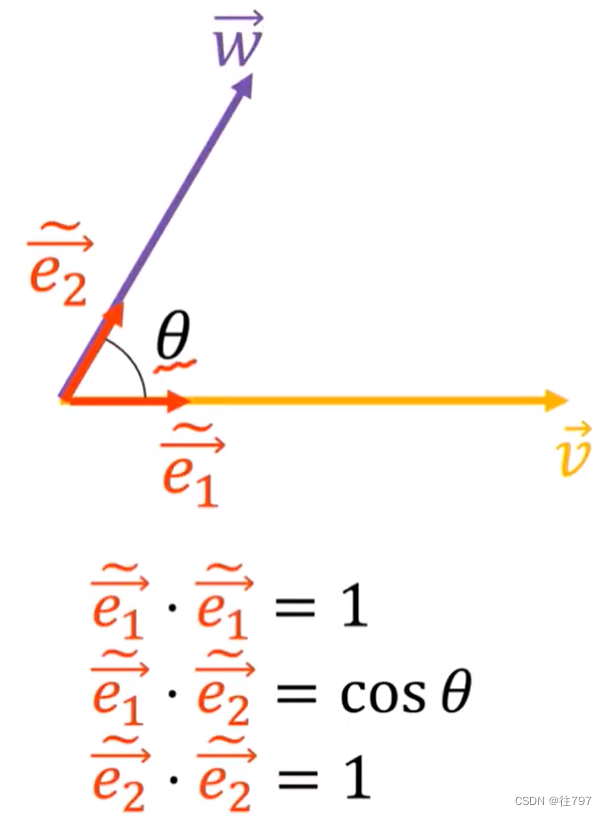
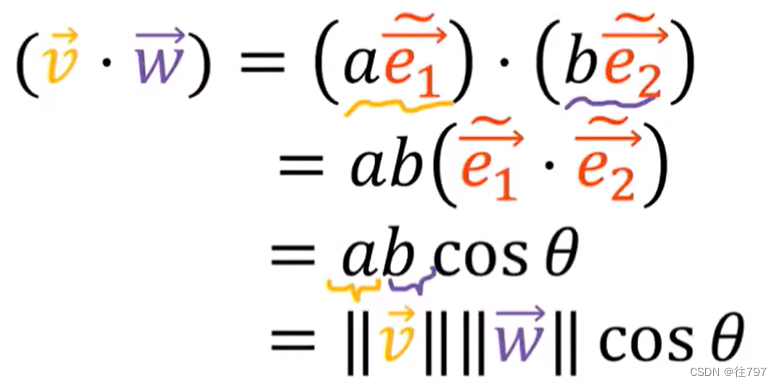
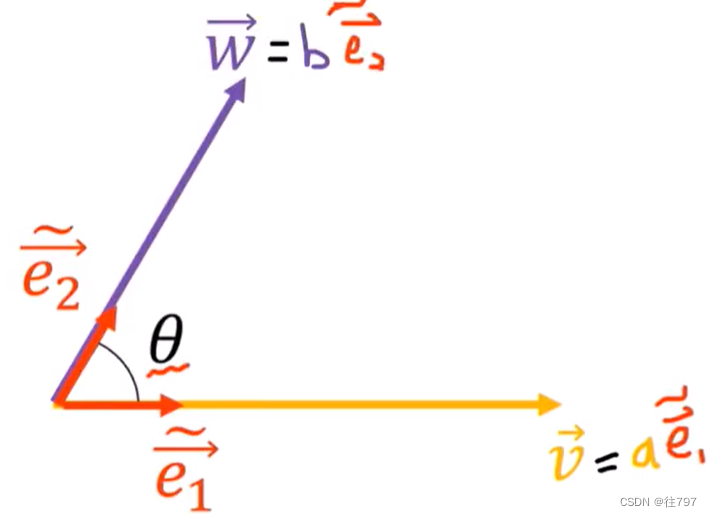
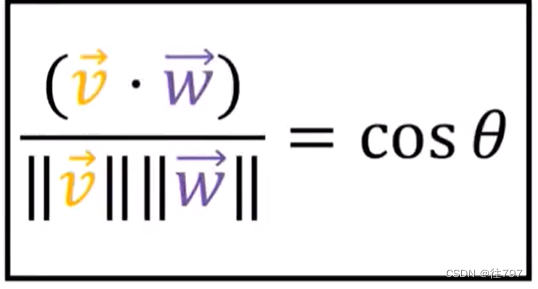
要求出V 和 W 的角度, 按照公式,只要求出 V · W ,以及她两的长度。
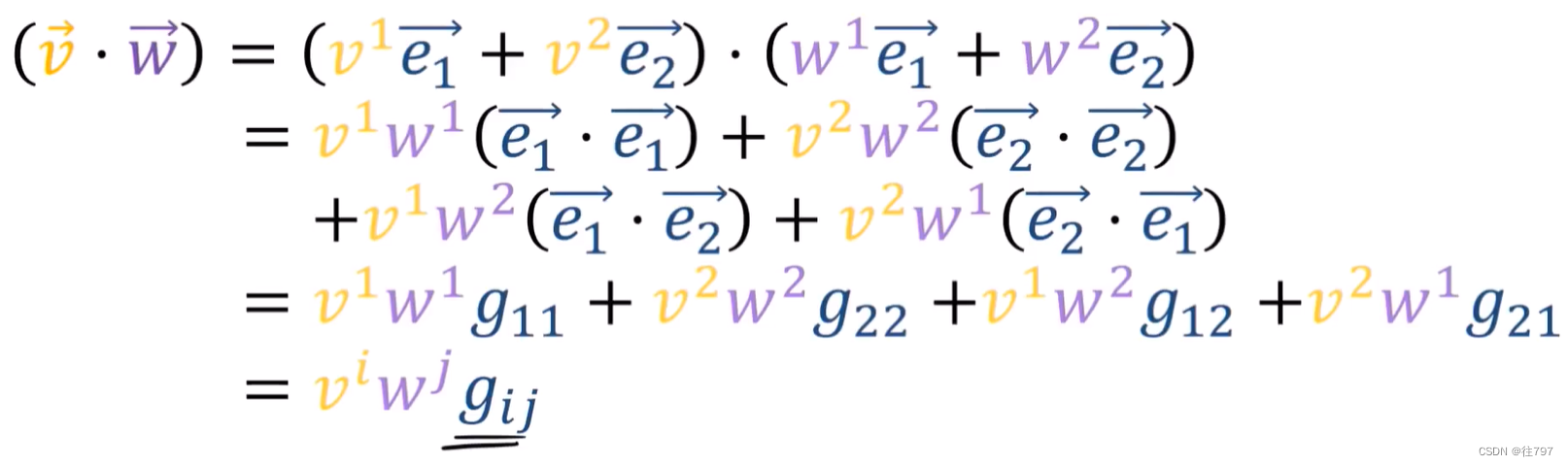
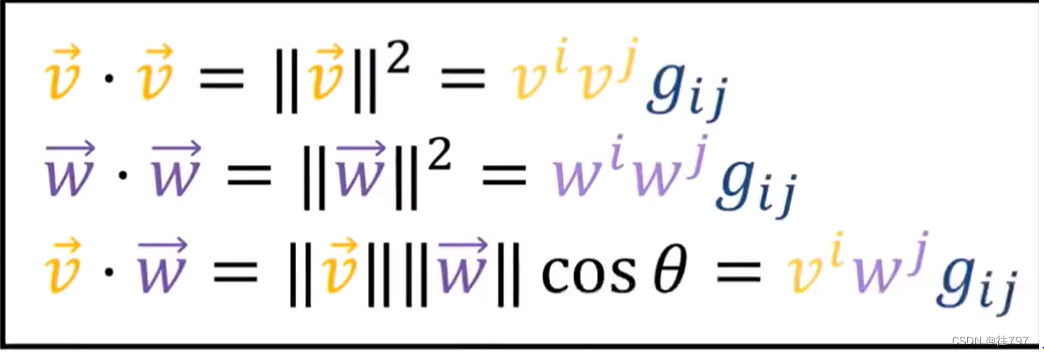
度量张量的用途
改变坐标系时,张量的分量是如何转换的?
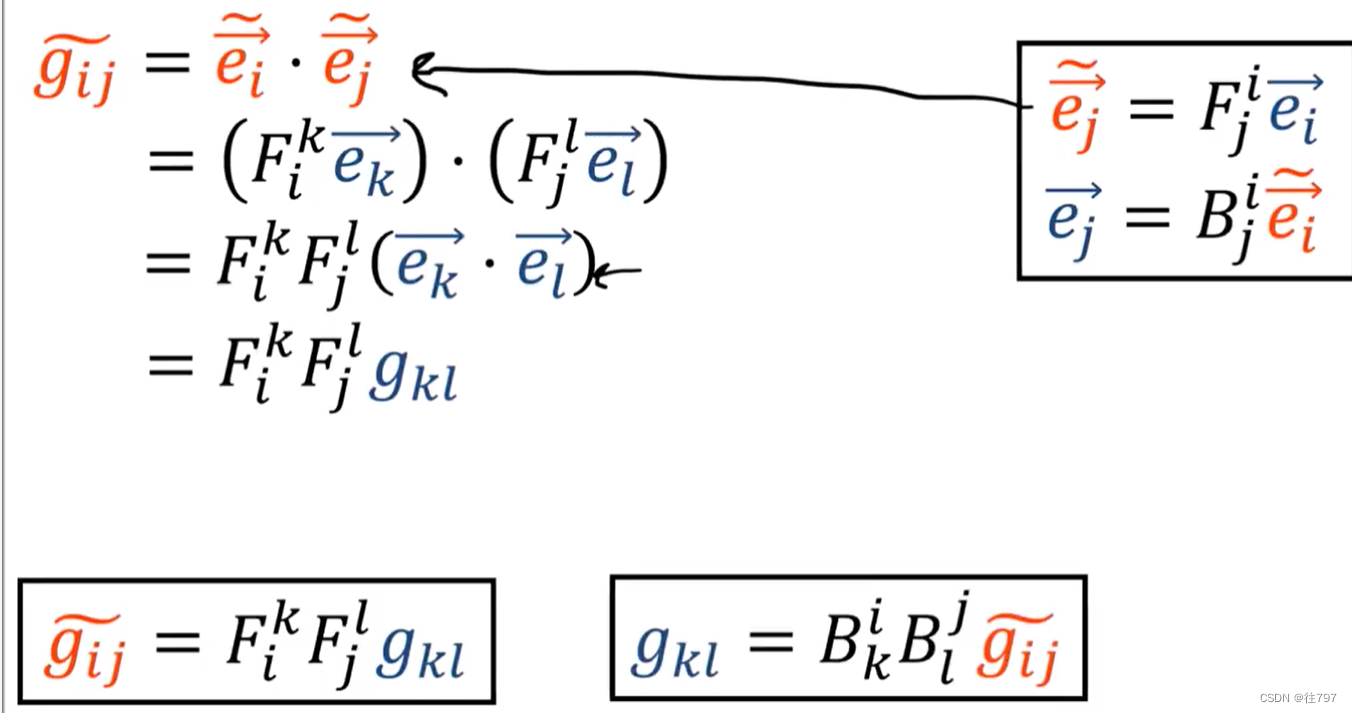
下面验证一下向量的长度在不同坐标系下(不同分量的度量矩阵),其长度保持不变。
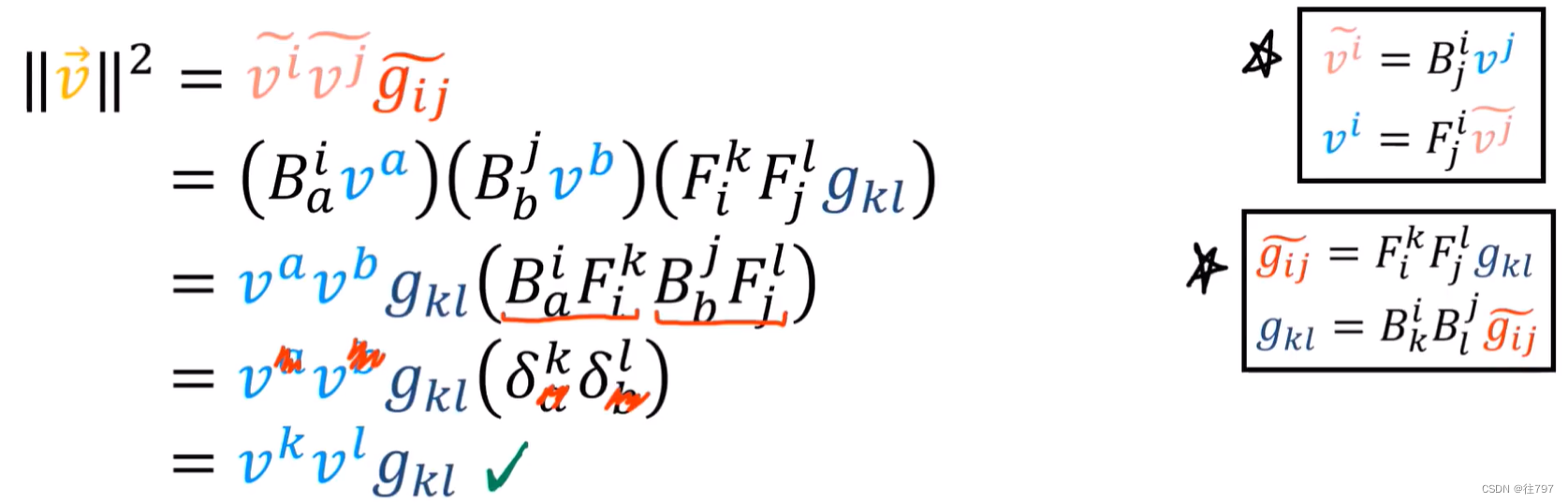
故使用度量张量的公式适用于所有坐标系,并且向量长度将保持不变。


巨大的规律,但是我还没悟出来, ,, 能写成这类形式的,都是张量,