目录
回顾二叉查找树
如何保证查找效率
B树的定义
提炼
B树的插入和删除
概括B树的插入方法如下
B树的删除
导致删除时，结点不满足关键字的个数范围时（需要借）
如果兄弟不够借，需要合体
回顾B树的删除
B+树
B+树的查找
回顾B+树
B+树与B树对比
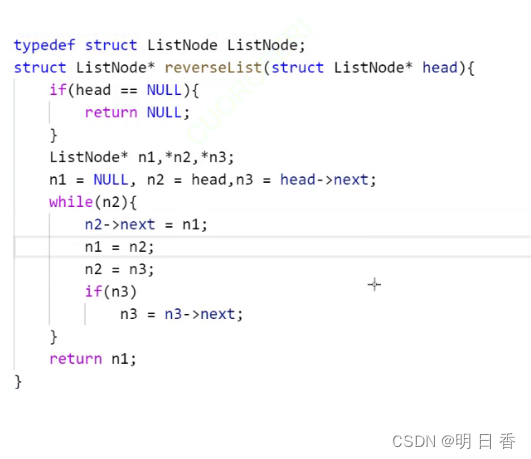
回顾二叉查找树
--能不能变成m叉查找树呢？
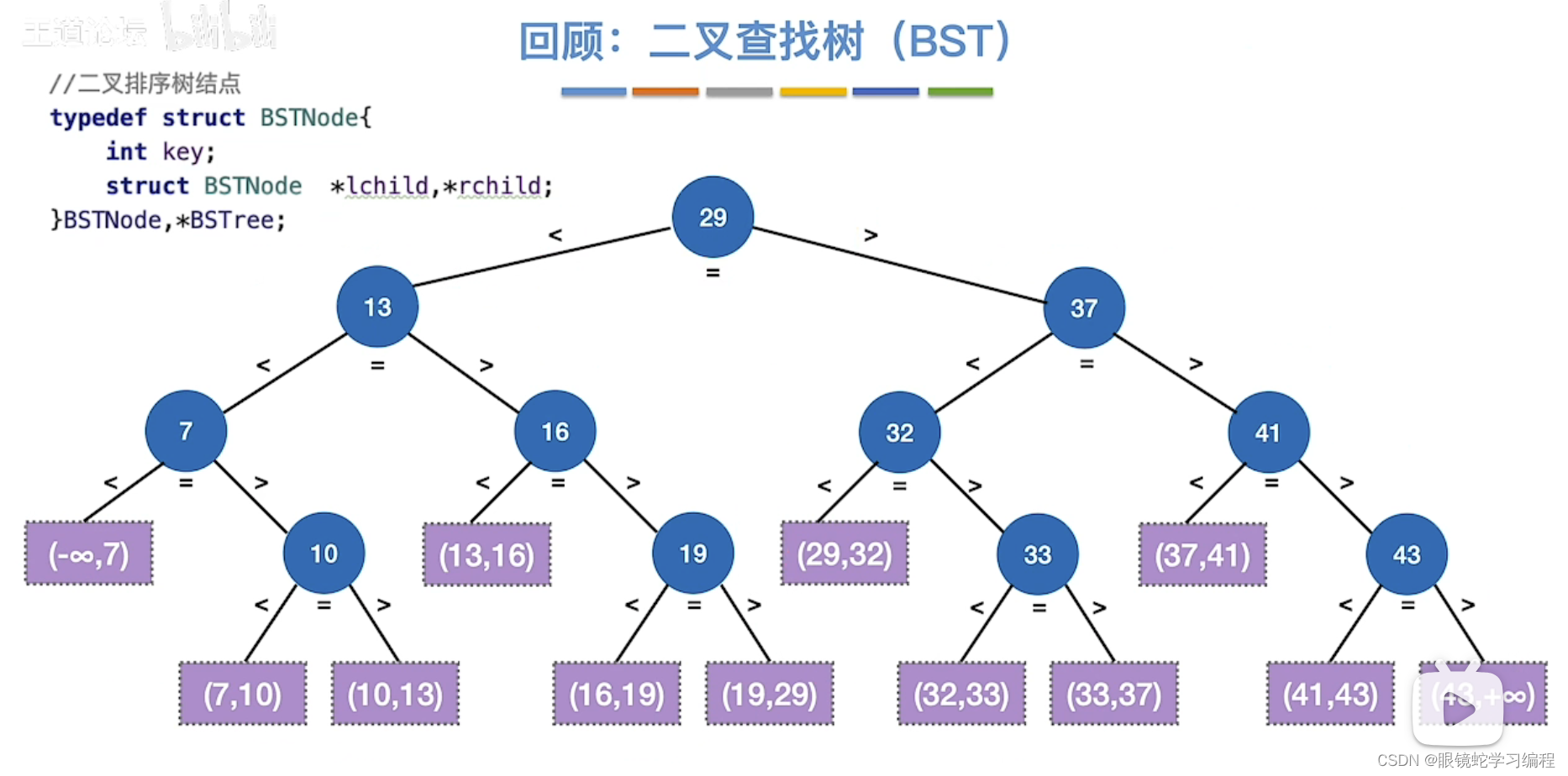
比如5叉查找树
紫色的是失败结点，每个子树内关键字结点都是有序的
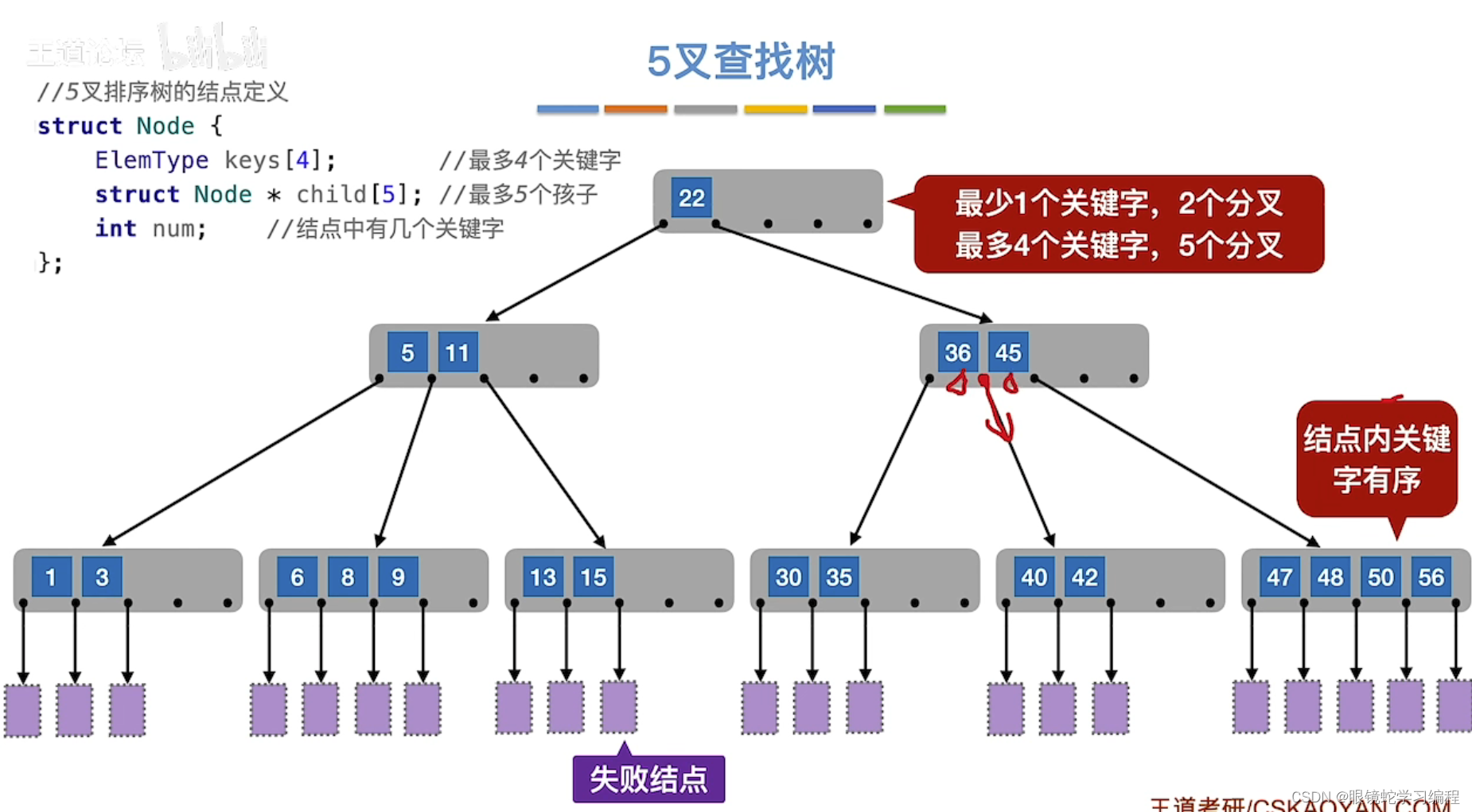
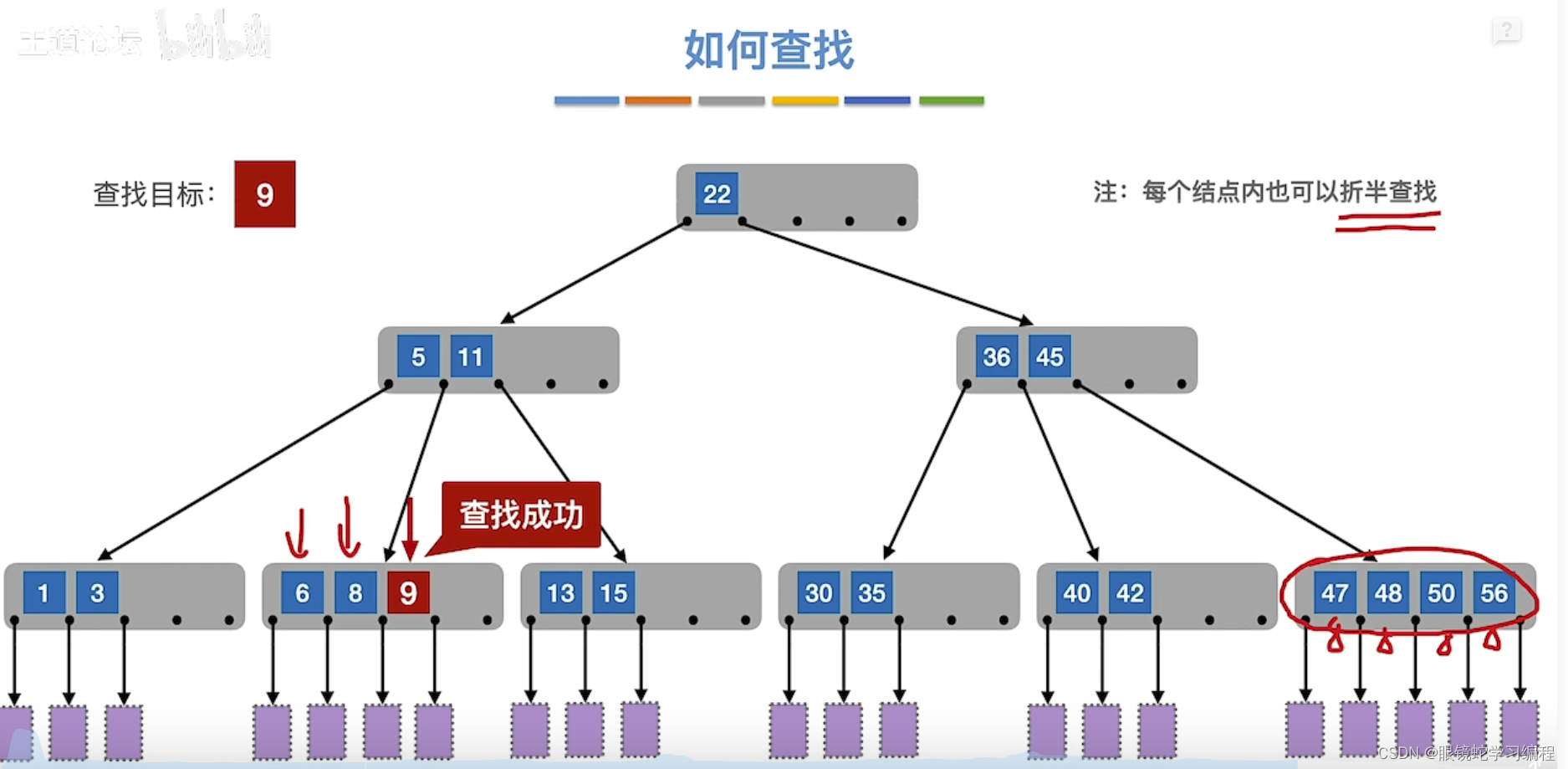
比如查找目标是9（查找成功的情况）
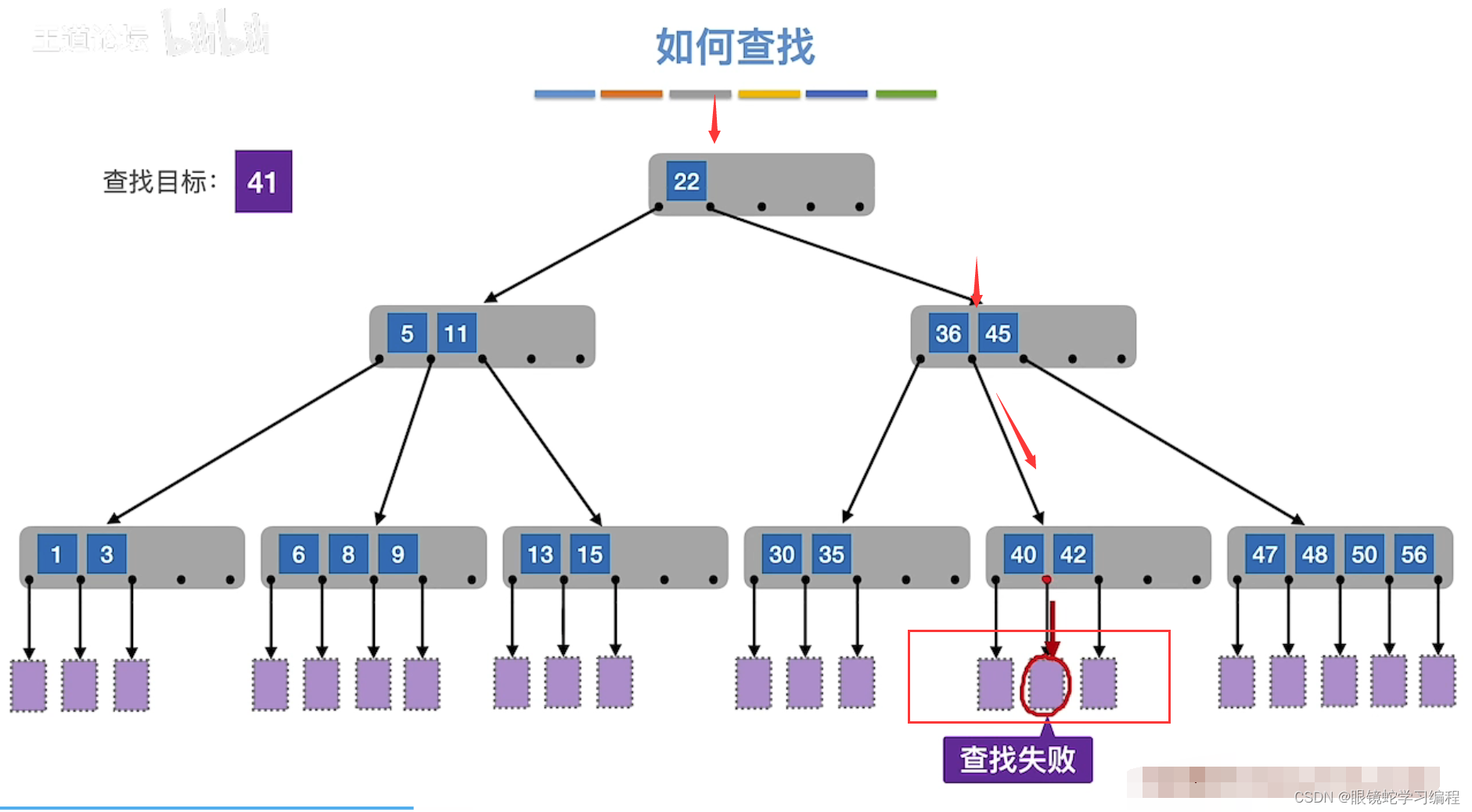
比如查找目标是（查找失败的情况）
对于查找失败就是最后找到的是NULL
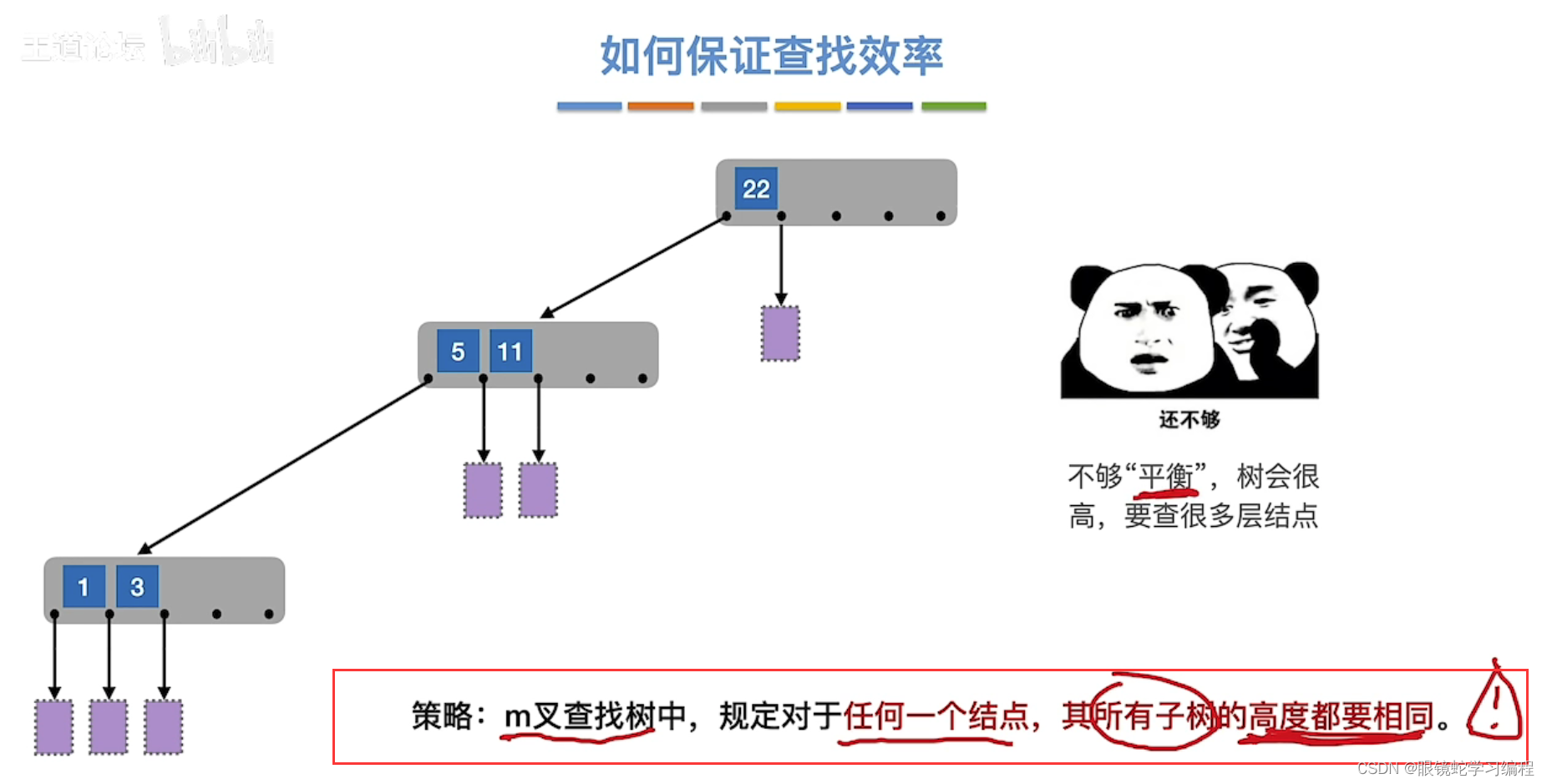
如何保证查找效率
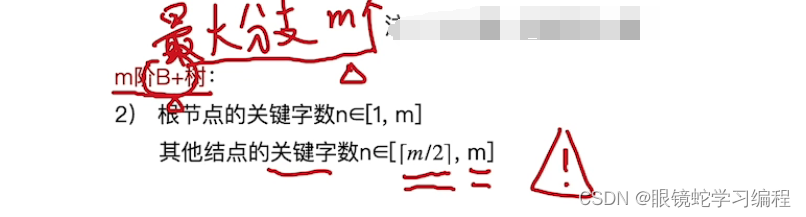
策略：m叉查找树，除了根节点外，任何结点至少有 m/2 （向上取整）个分叉，即至少有m/2（向上取整）-1个关键字
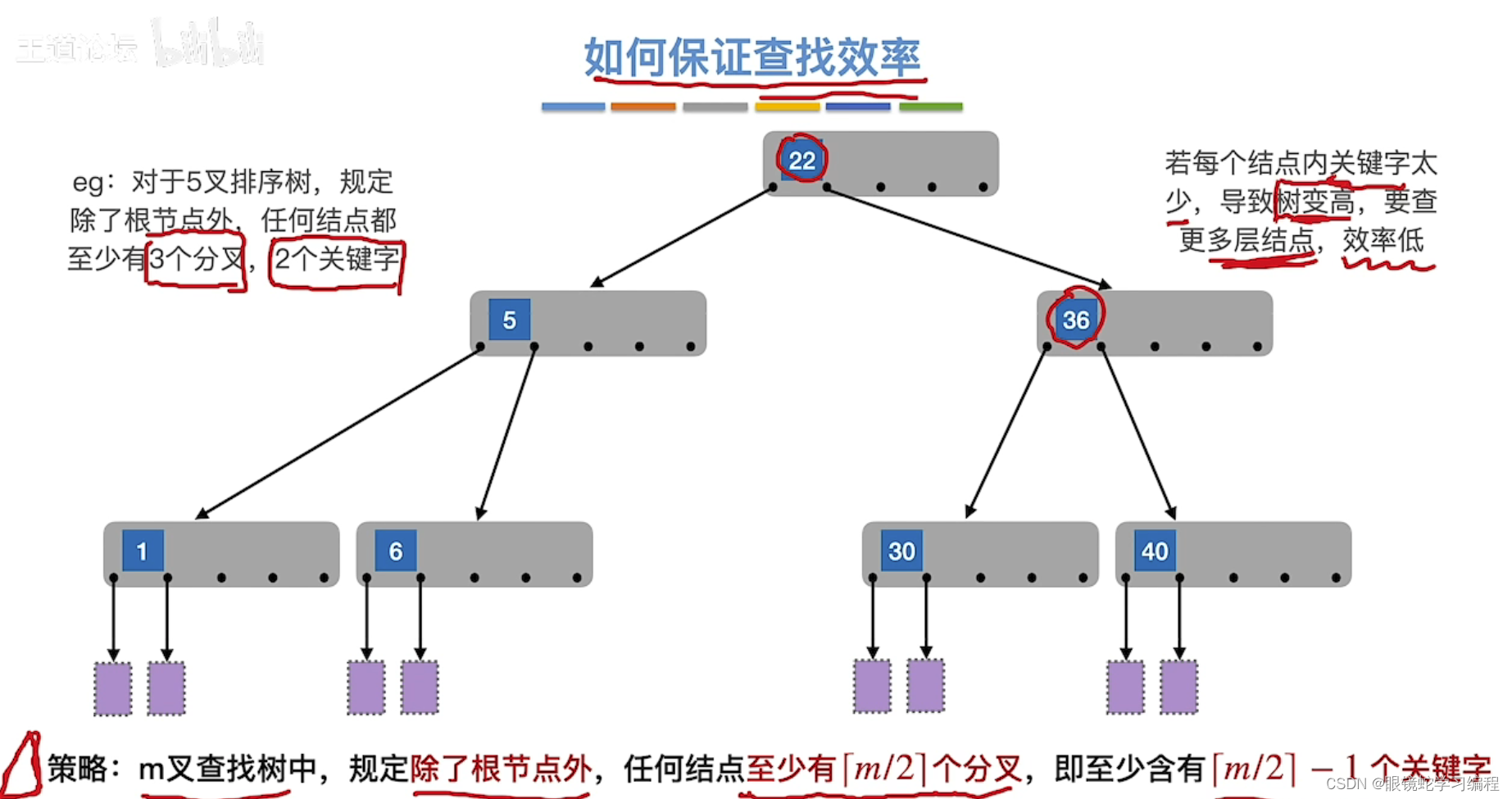
为什么要除了根节点呢？原因如下:
所以如果可以规定一个下限，（1）分叉不是特别少，（2）同时高度都要相同（即绝对平衡）
满足这两个条件那么就是一颗B树
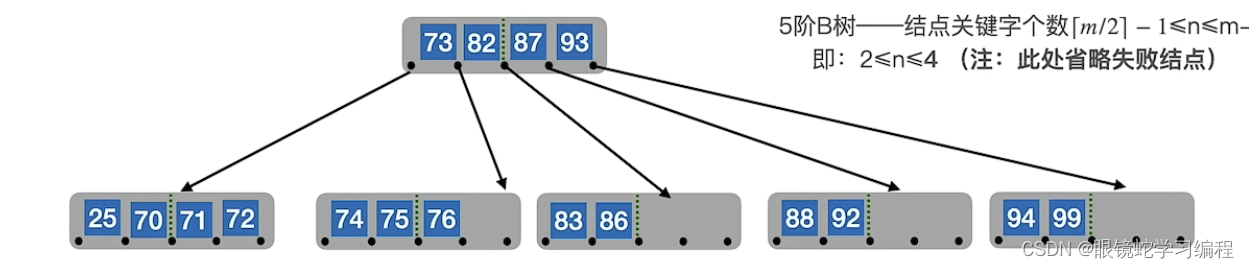
如下图就是一颗5叉的B树
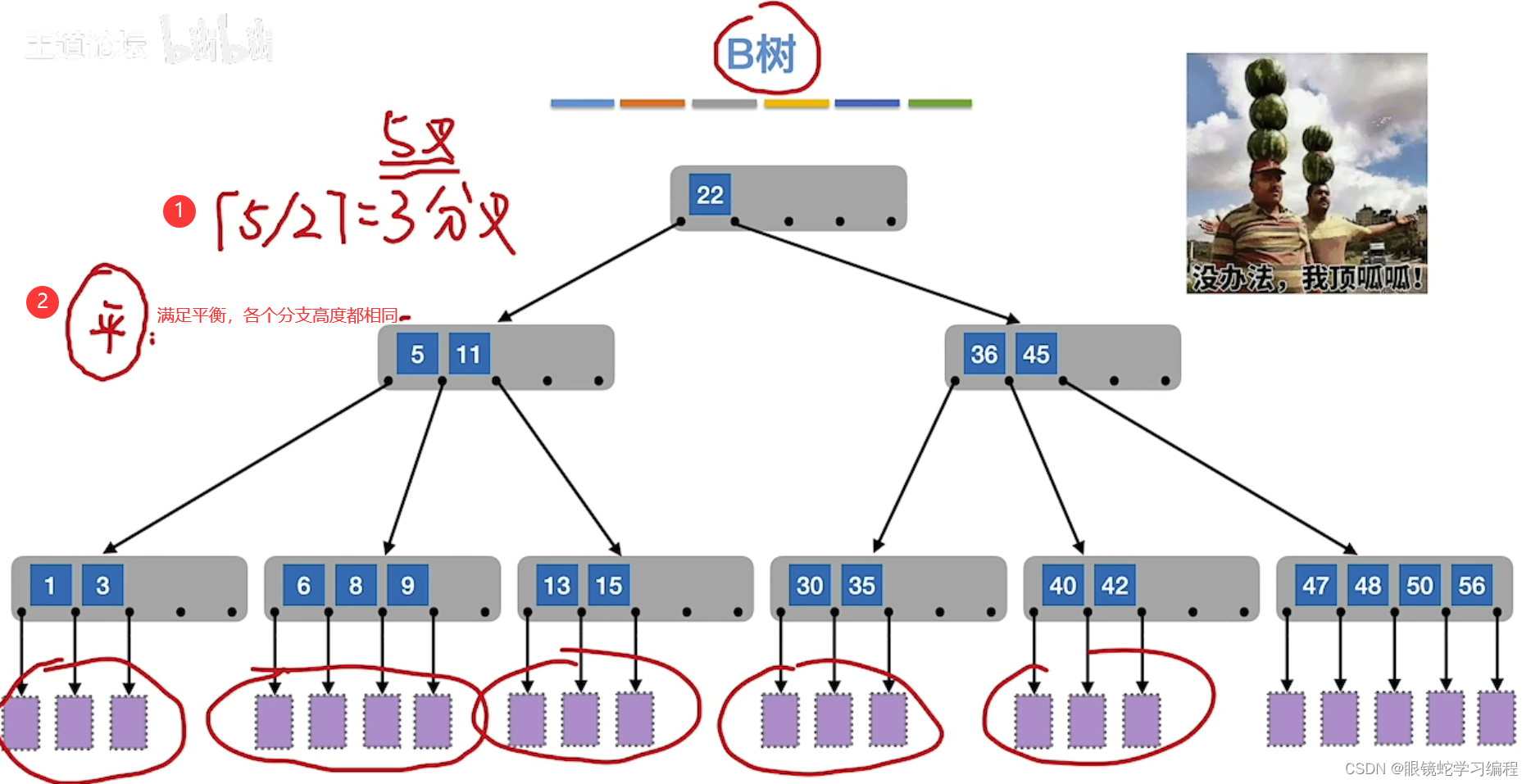
接下来是时候展示B树的定义了！！！！！！！！
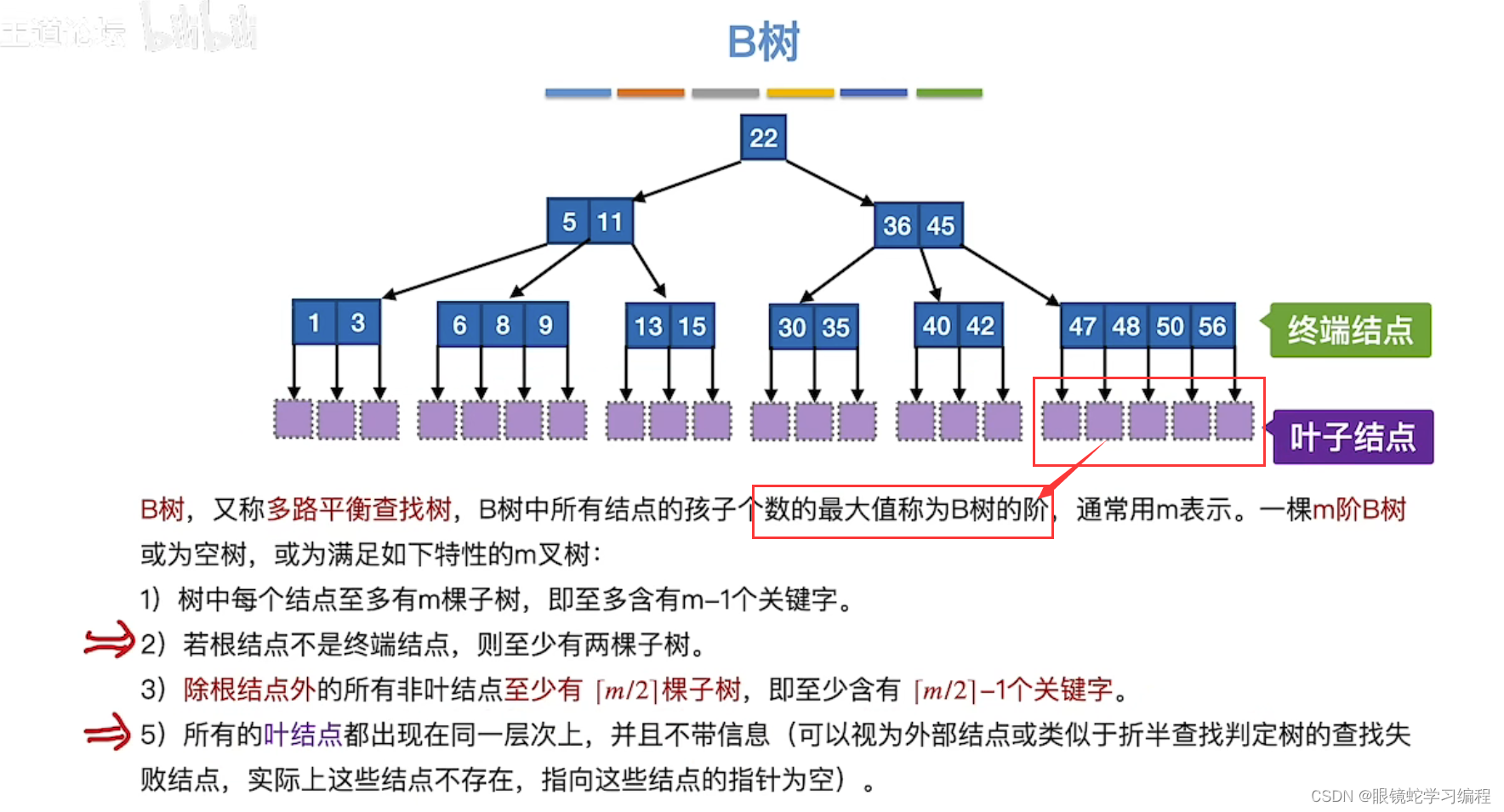
B树的定义
提炼
（自己可以容易理解的整理）
绝对平衡，是没有高度差的
终端结点：包含信息
叶子结点（本质就是失败节点，它是个空指针）：不包含信息
分叉个数最多的就是阶，图中分叉最多是5个，所以是5阶
2）若根节点不是终端结点，则至少有两颗子树的原因：是保证绝对平衡，没有高度差
5）所有叶结点都出现在同一层原因：是保证绝对平衡，没有高度差
4)K是关键字，P是指针，n是记录实际关键字到底有几个；K1<K2<....Kn是说关键字必须有序(这里是递增，也可以递减，只要有序即可)
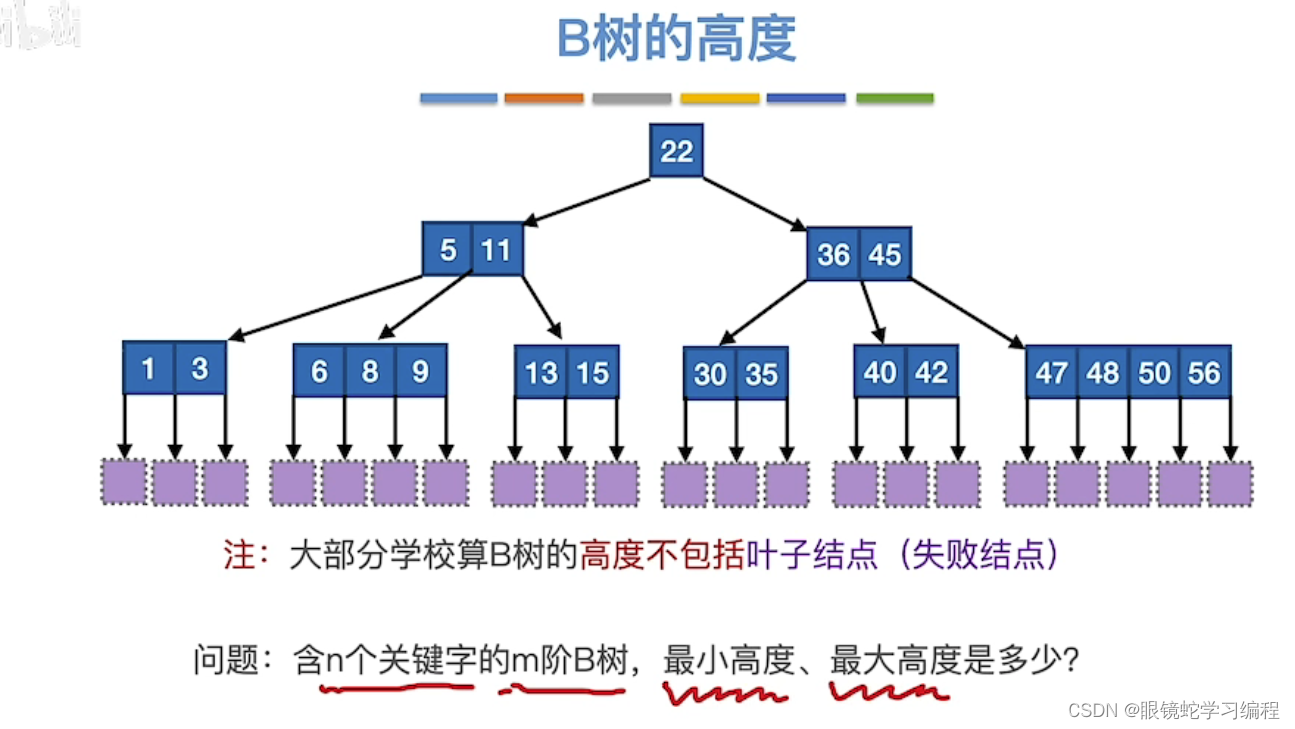
最小高度的计算
最大高度的计算
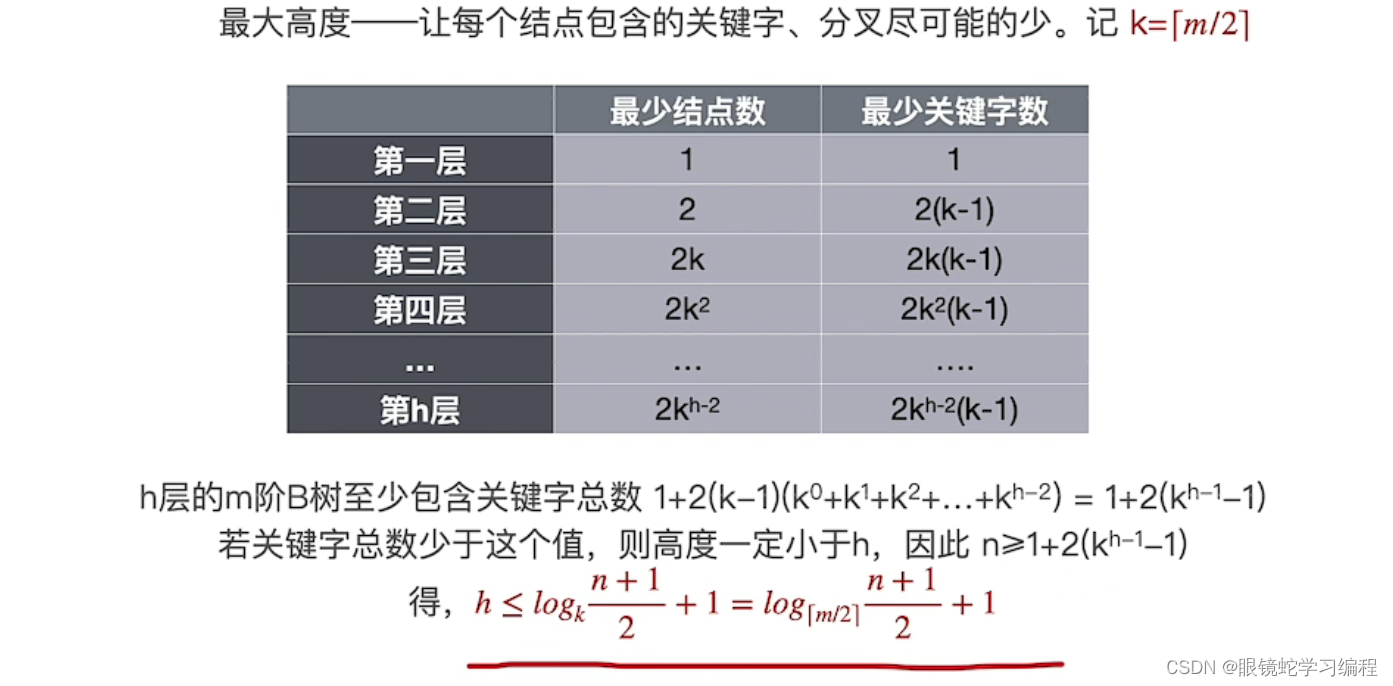
B树的本节总结
B树的插入和删除
以5阶的插入来演示过程
依次放 25，38，49，60，
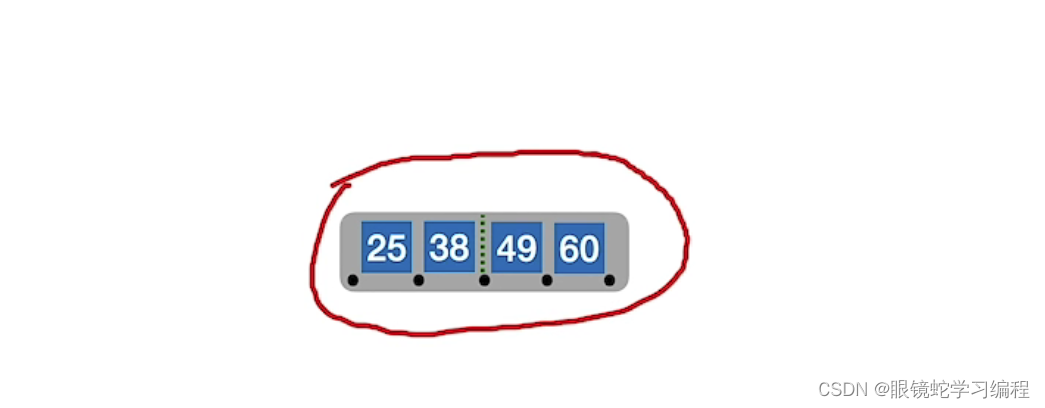
放80，导致关键字超出了4个
此时要进行分裂
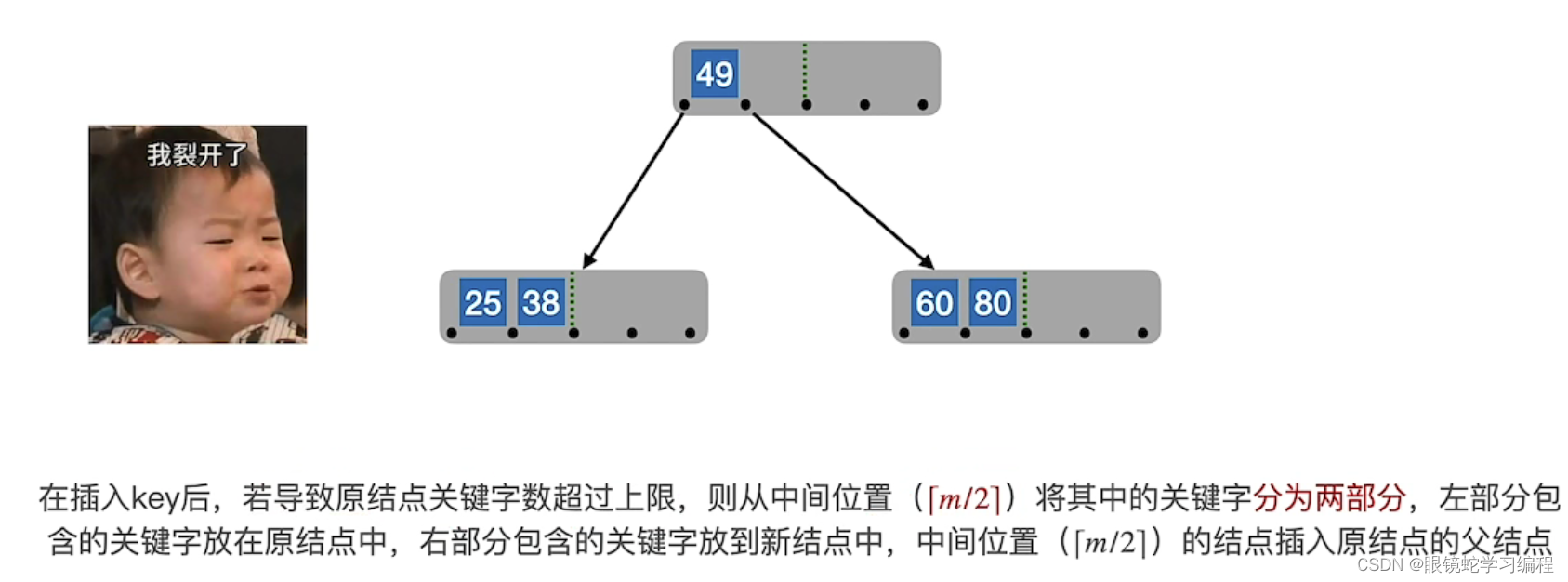
新元素一定是插入到最底层“终端结点”，用“查找”来确定插入位置
插入要保证这个结点的左边结点要比其小，右边要比关键字大
接着插入90
90的正确的插入位置应该如下，接着插入99
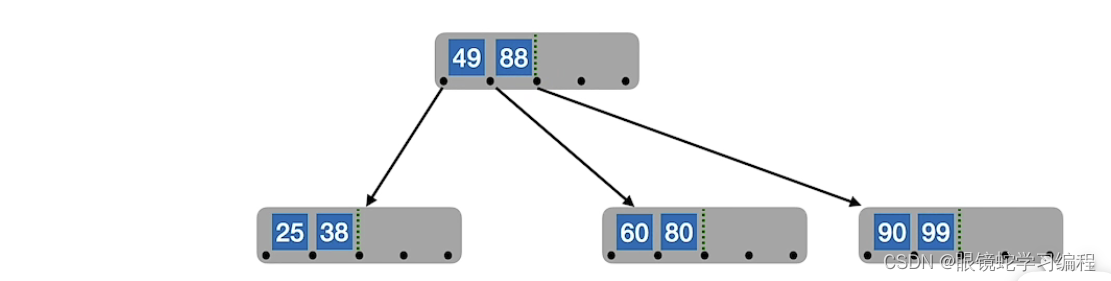
接着插入88
所以插入88的结果如下
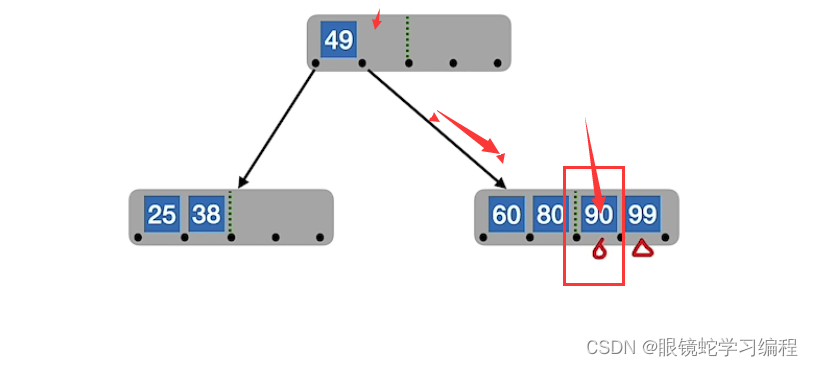
接着插入70，83，87肉眼可见往最低层插入，发现出现了溢出，将关键字[m/2]（向上取整）分成两部分即87位置
即最终插入80的位置如下
接着插入如果导致父节点也出现溢出，接着分裂，直至传到根节点为止。
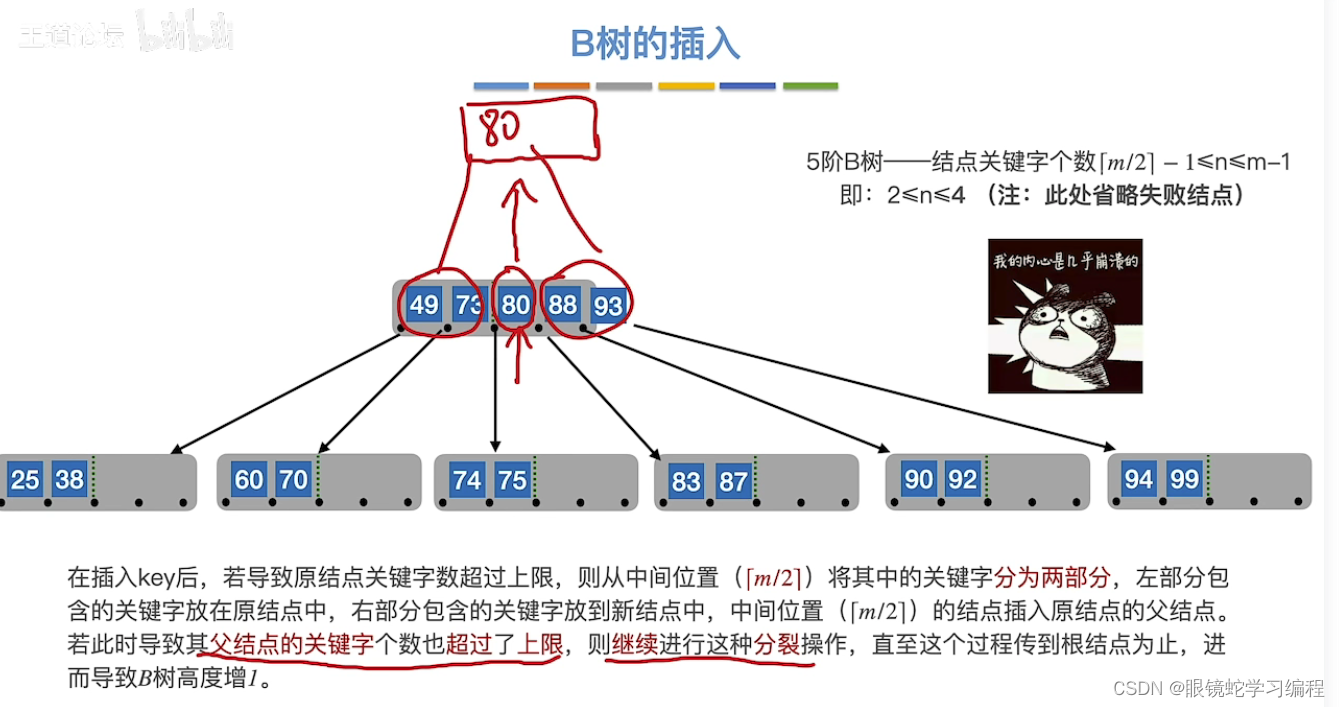
概括B树的插入方法如下
B树的删除
（1）删除60
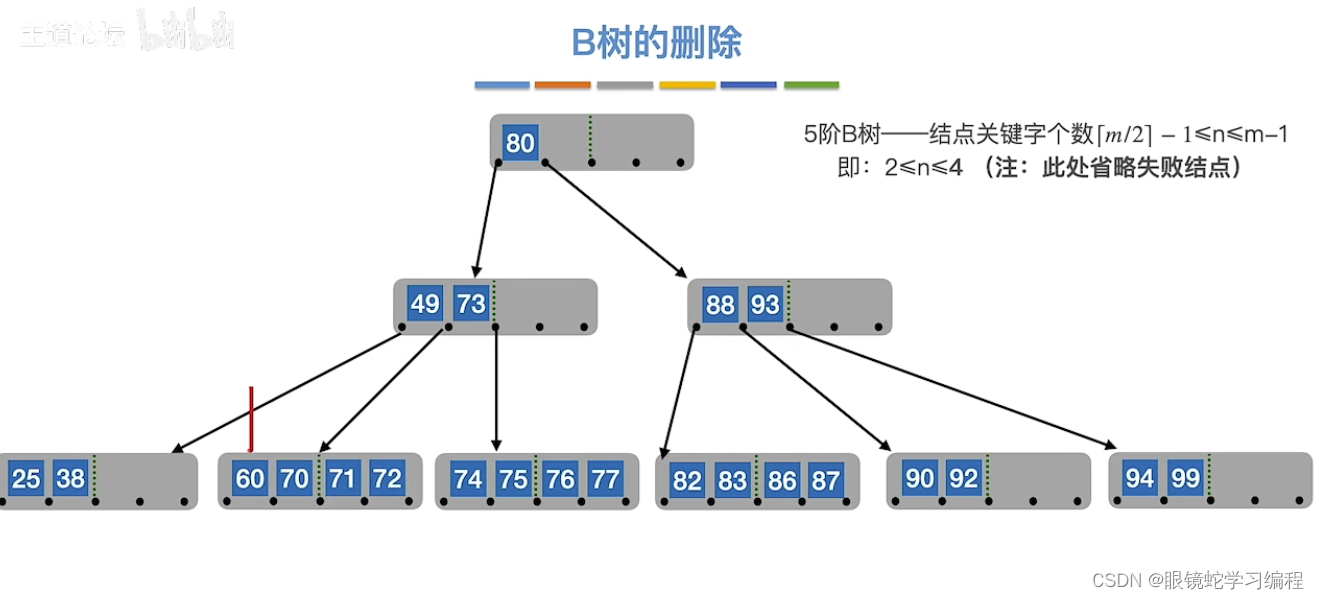
删除结果如下
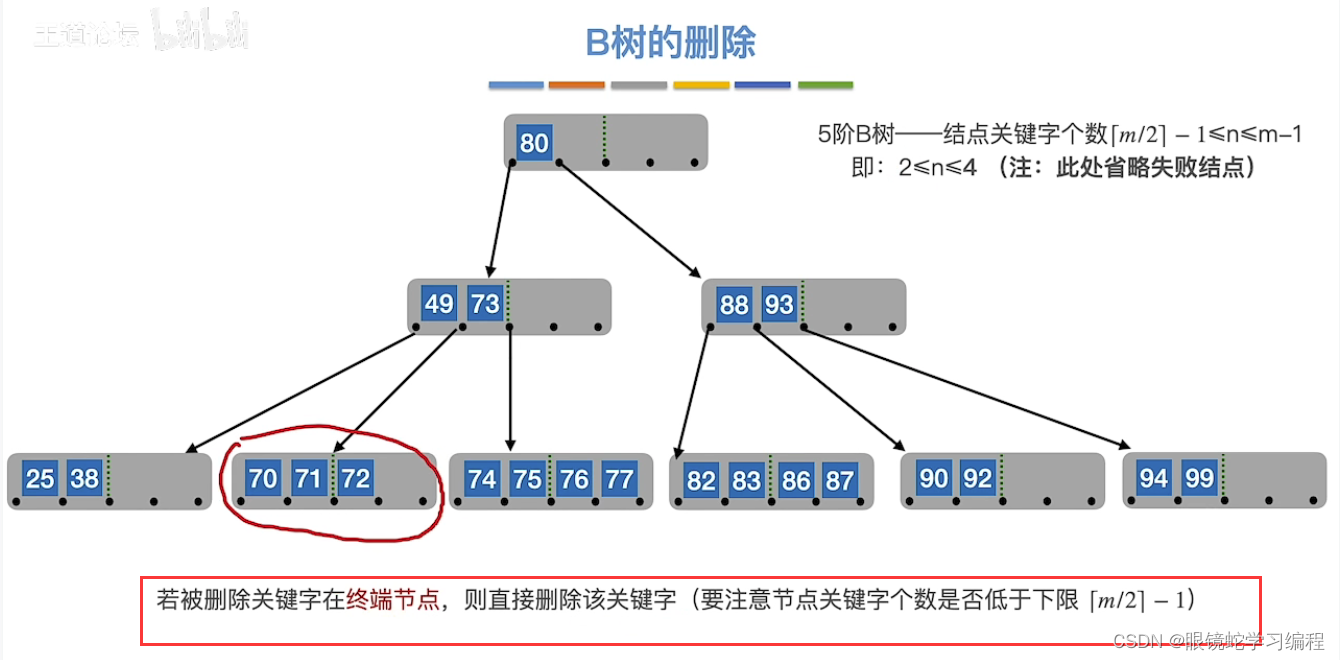
如果删除80结点，会导致根结点为空
方法找直接前驱或者直接后继
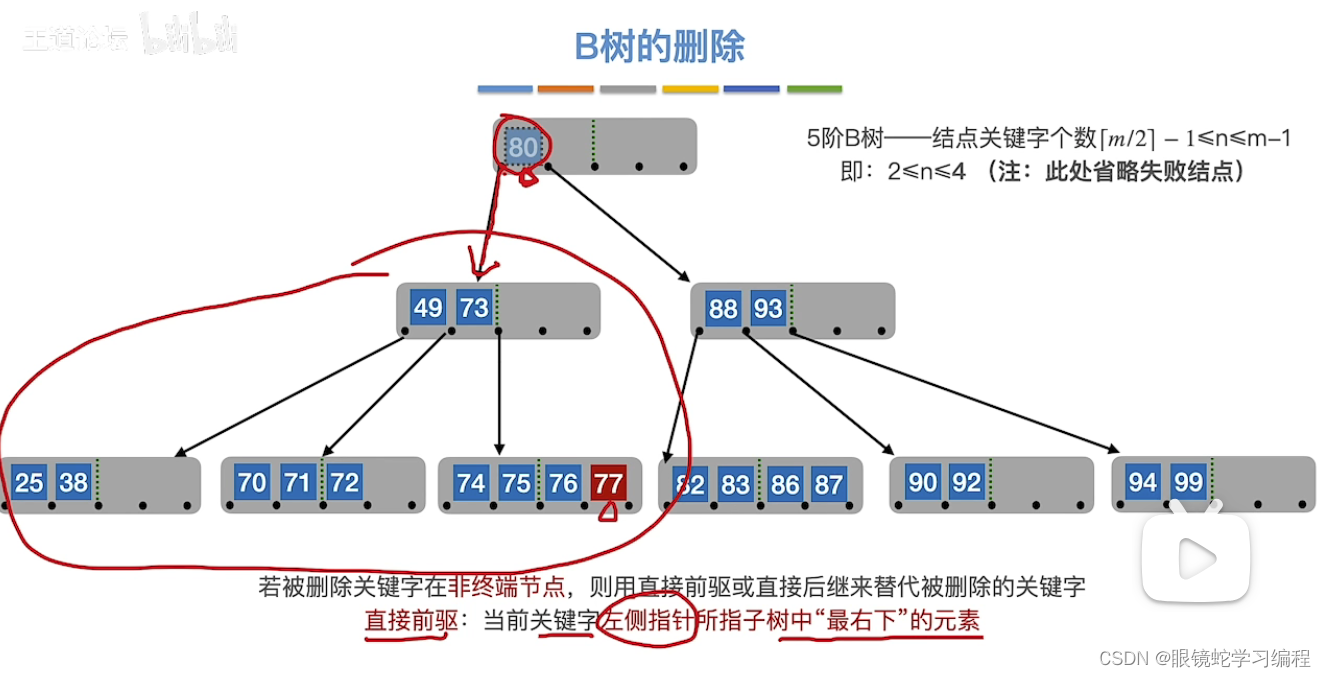
此时用直接前驱70替代了80的位置，如下图
找直接前继的发法：关键字左侧指针所指子树中“最右下”的元素
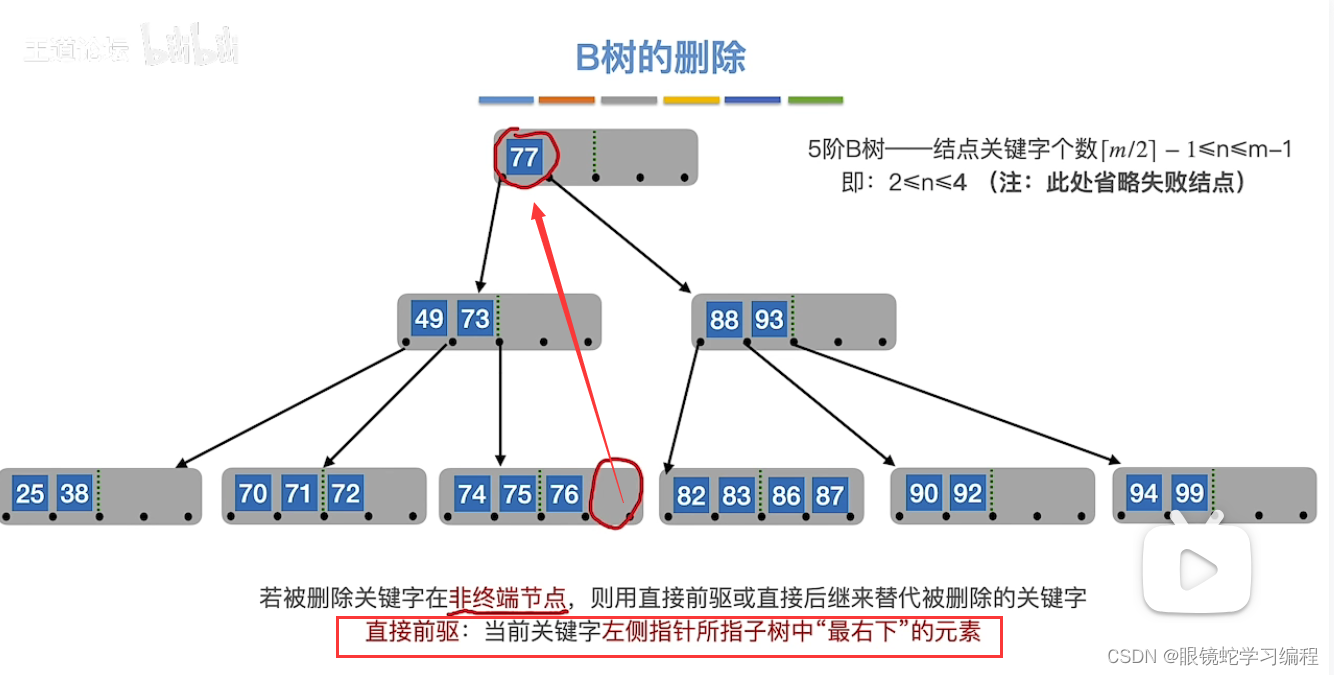
接着删除77，如果利用77的直接后继，替代删除的元素77
找直接后继的发法：关键字右侧指针所指子树中“最左下”的元素
对非终端结点关键字的删除，必然可以的转化为对终端结点的删除操作
导致删除时，结点不满足关键字的个数范围时（需要借）
比如删除38后，导致结点不满足关键字的个数范围2<=n<=4时,需要借，如果借右兄弟时
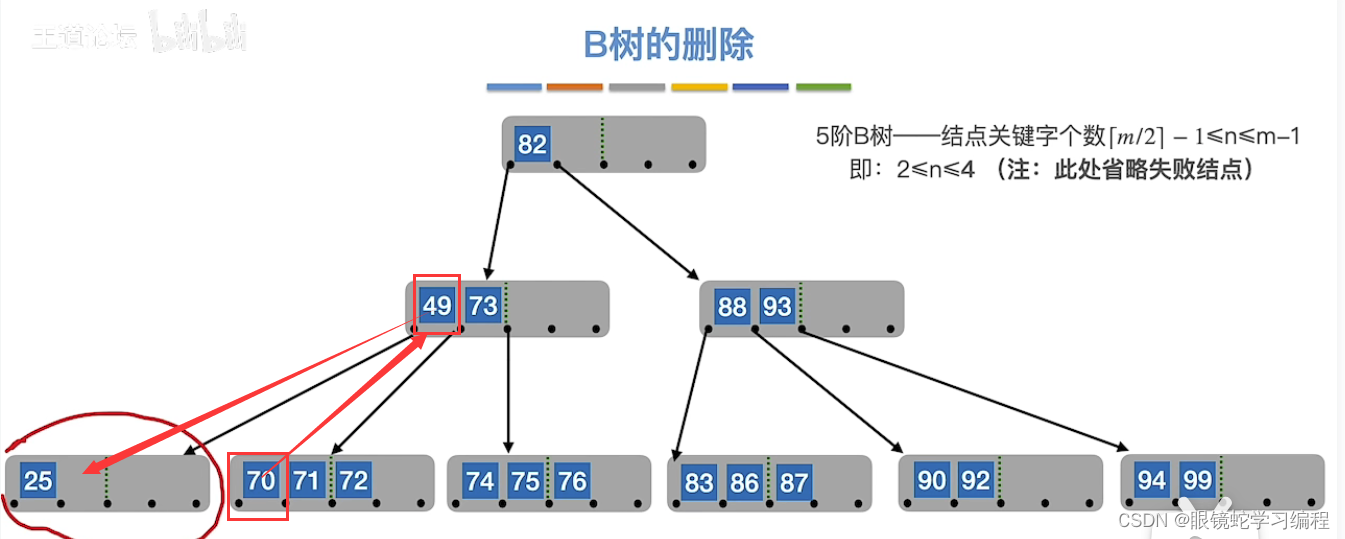
删除结果如下
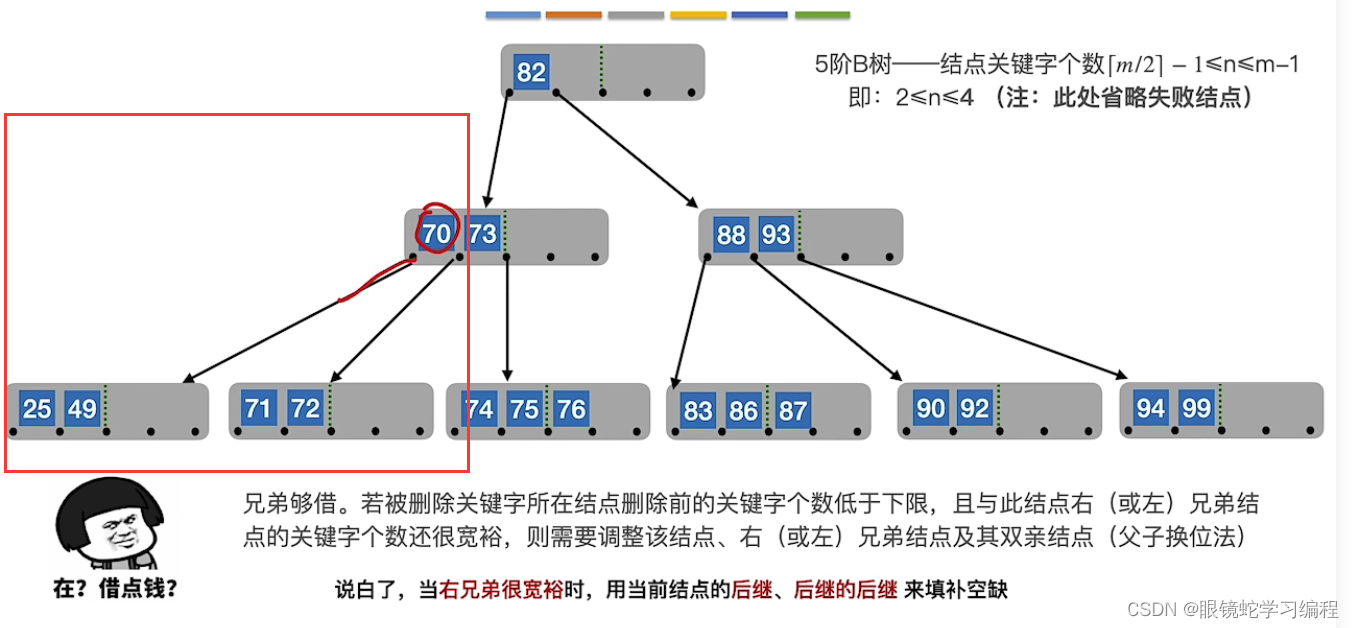
删除90后，导致关键字只剩下92，不在范围内，同时右兄弟手头紧张时，现象如下
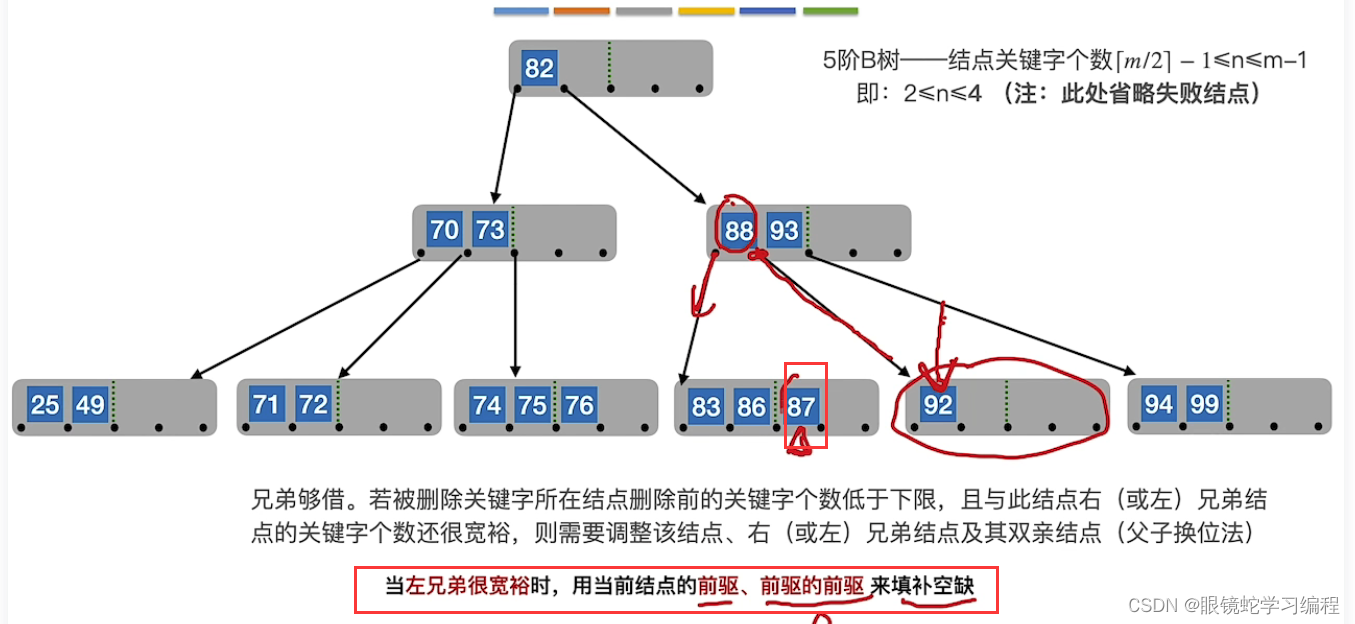
借左兄弟
92的前驱所连指针是88，88前驱是左孩子的最右边结点87，用88插入到92前面，再用87替代88位置，
删除92后的最终结果B树是
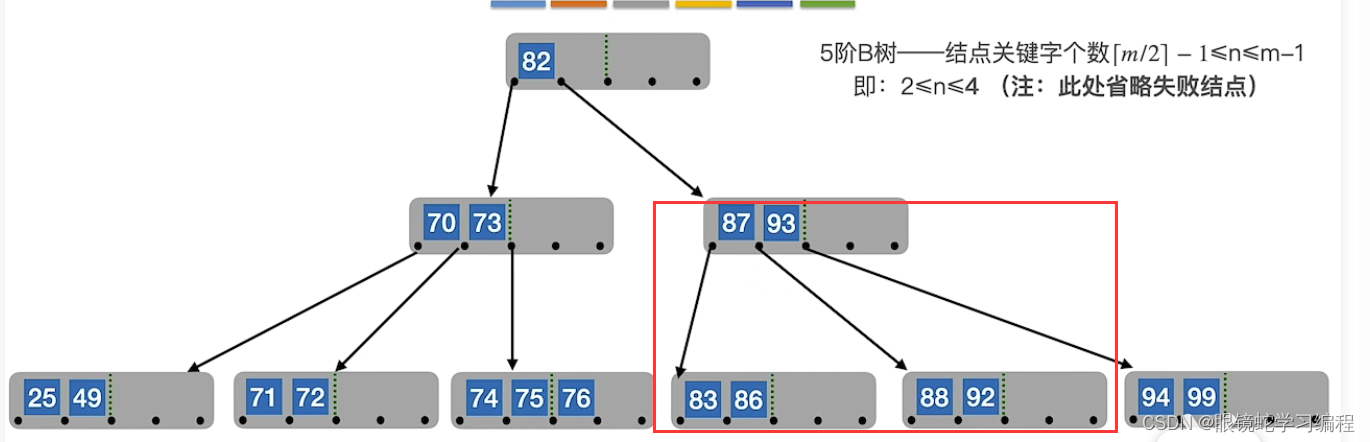
关键：
要永远保证 子树0<关键字1<子树1<关键字2<子树2<
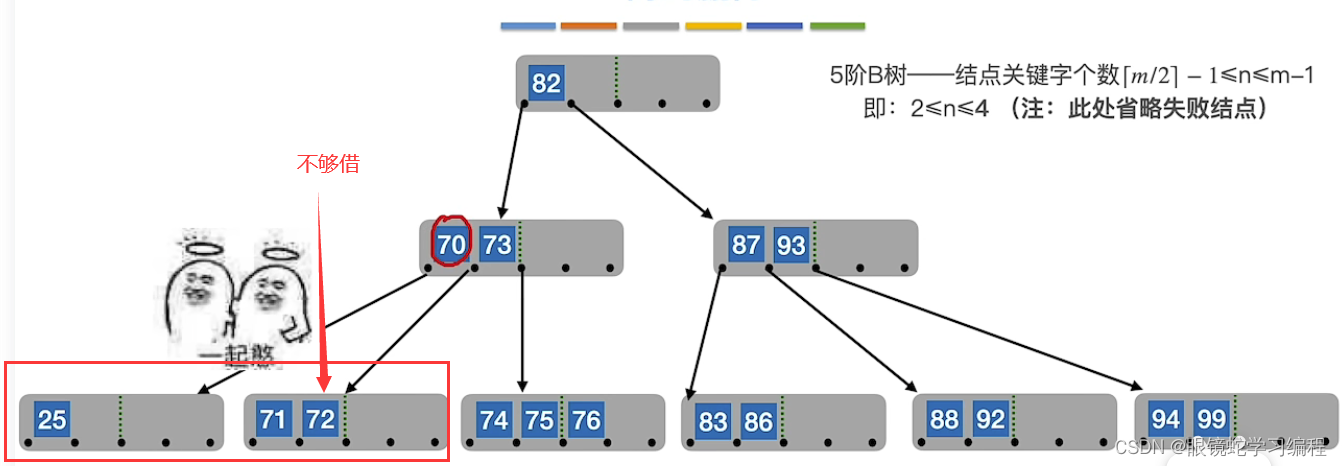
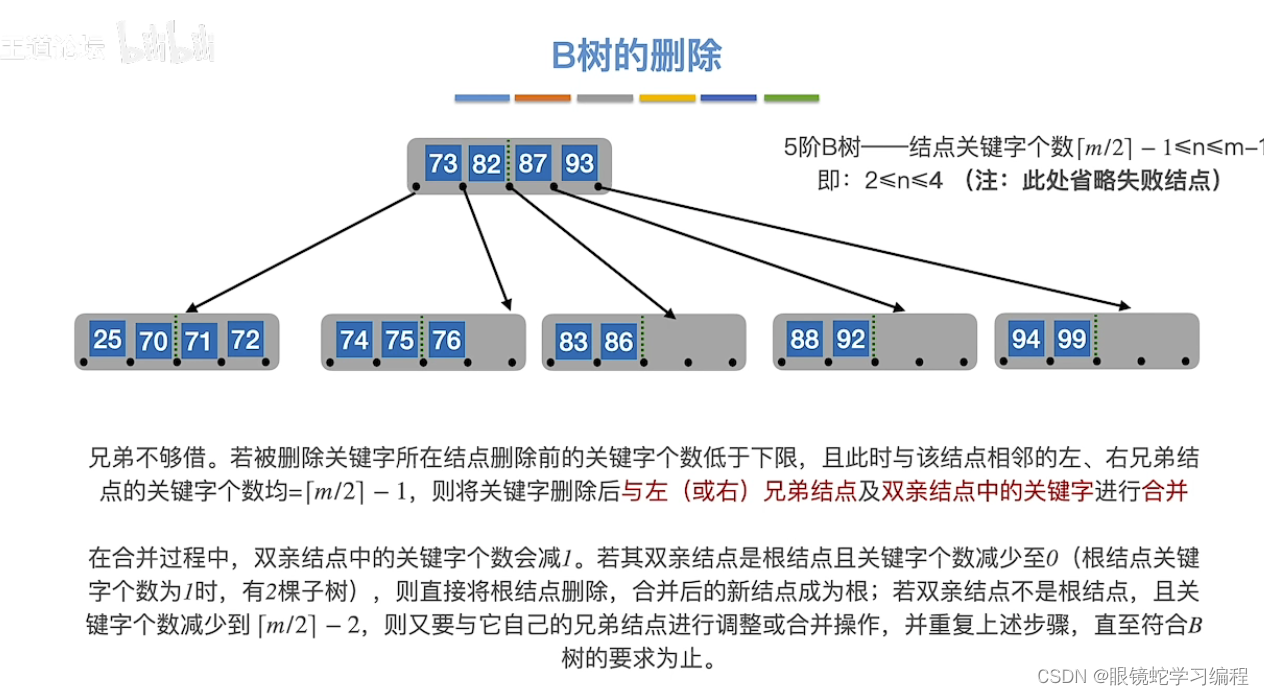
如果兄弟不够借，需要合体
如果删除49后形成如下情况，左右兄弟不够借
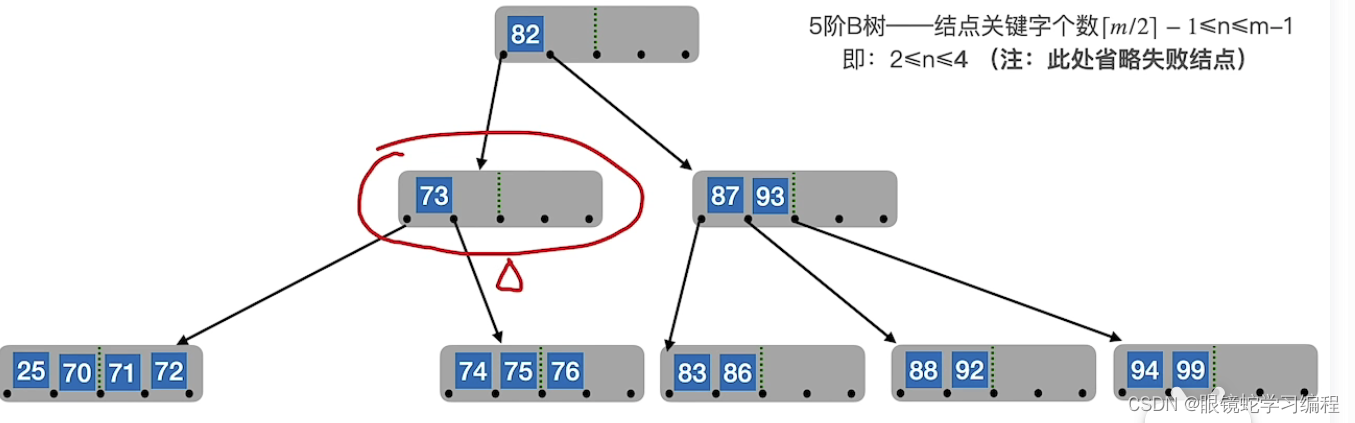
开始合并，但是要永远保证 子树0<关键字1<子树1<关键字2<子树2<，从父节点要来70，但是导致父节点又不够了
接着合并
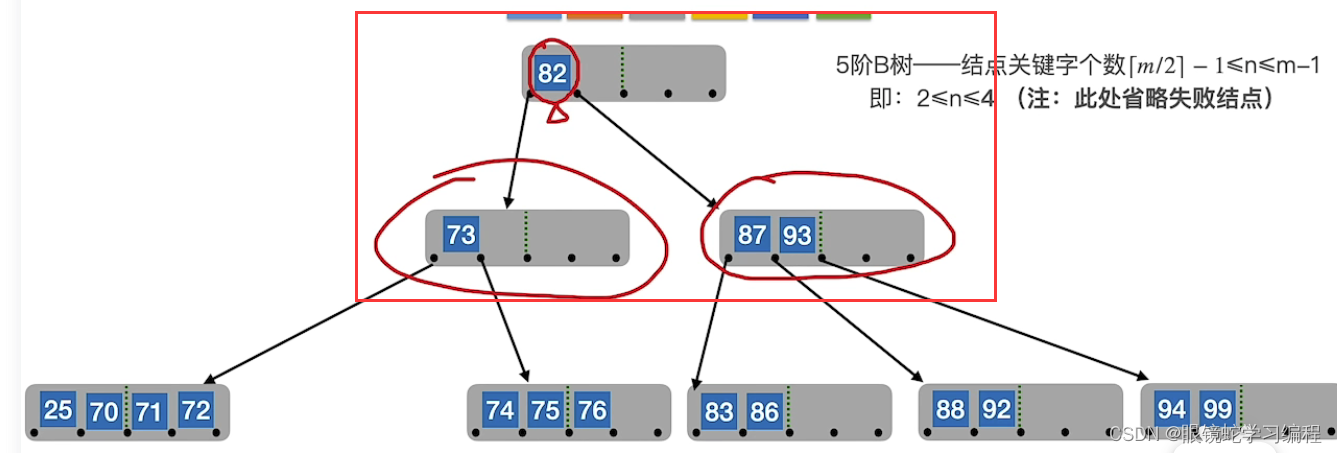
删除最终的结果如下：
回顾B树的删除
B+树
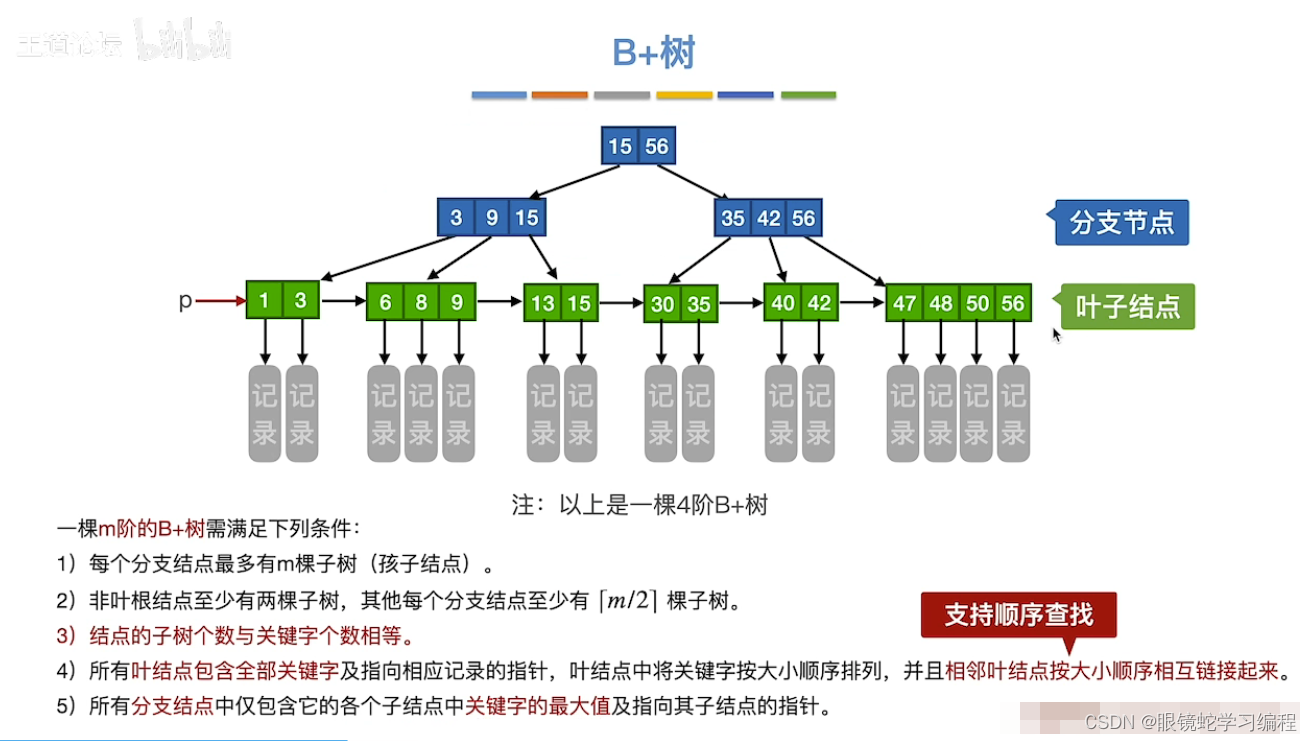
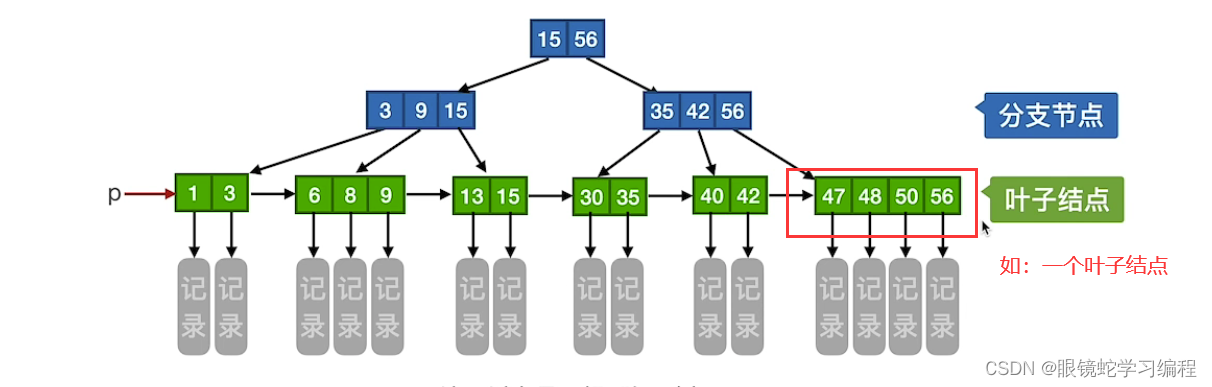
上一层的一个关键字是其子树对应的最大值，比如叶子结点中1，3，最大的的是3，所以的父节点的一个关键字是3。接着叶子结点6，8，9最大的的是9，所以的父节点的另一个关键字是9，同理，从下往上找最大的值，作为上一层的一个关键字
注意的点：
3）重点：B+树的结点的子树个数与关键字个数相等
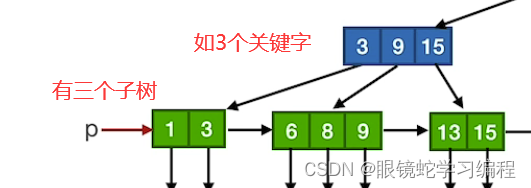
而B树如果有2个关键字是有3个子树的，如下图
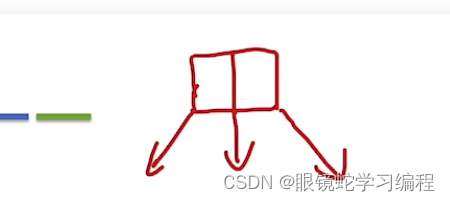
4）叶子结点是整个的一块，比如47，48，50，56这个整体，并不是里面的某一部分，所以一个叶子结点可能包含m个关键字
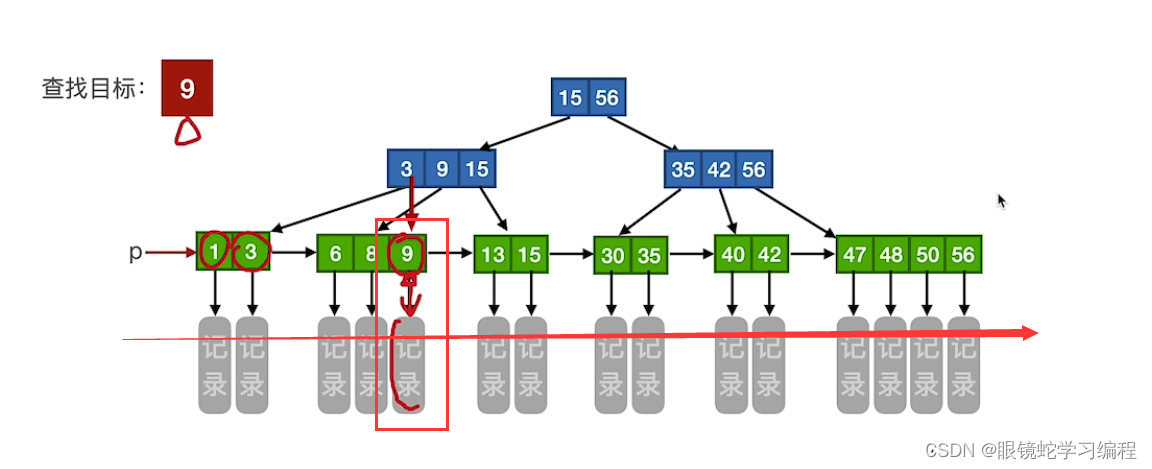
B+树的查找
方式（1）
通过根节点往下查找，但是必须找到最下层，即叶子结点才可以，因为叶子结点才记录信息
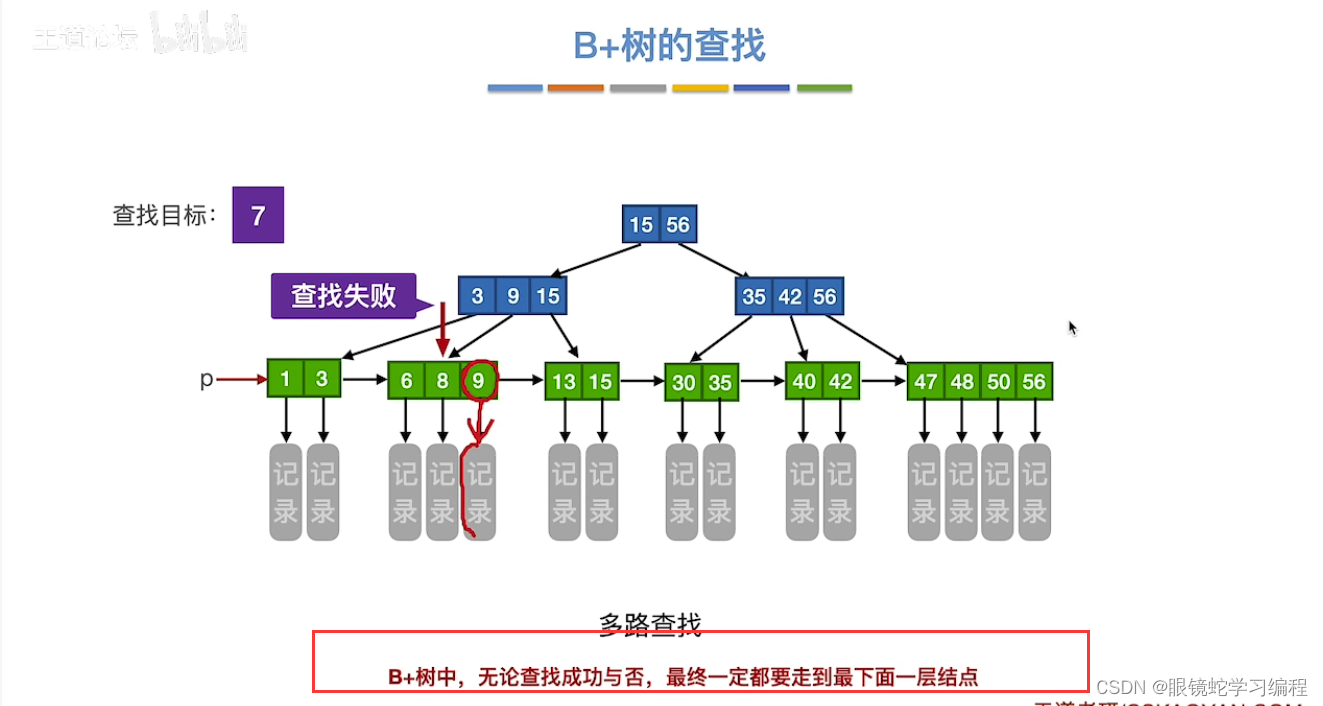
方式2
可以从保存的指针p，查找
回顾B+树
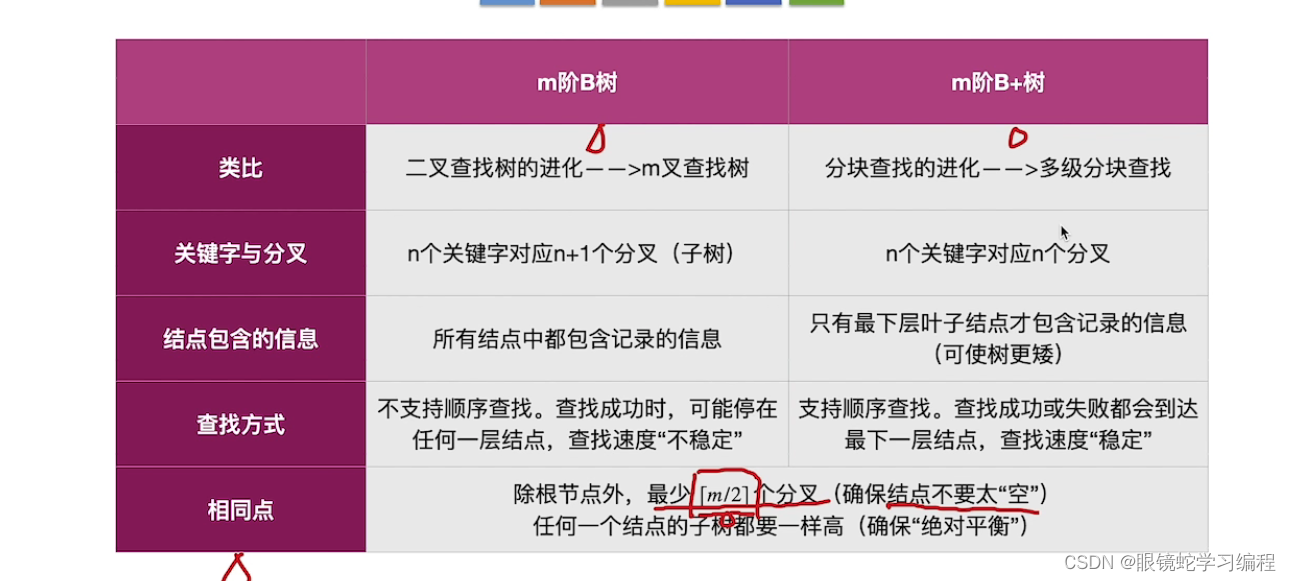
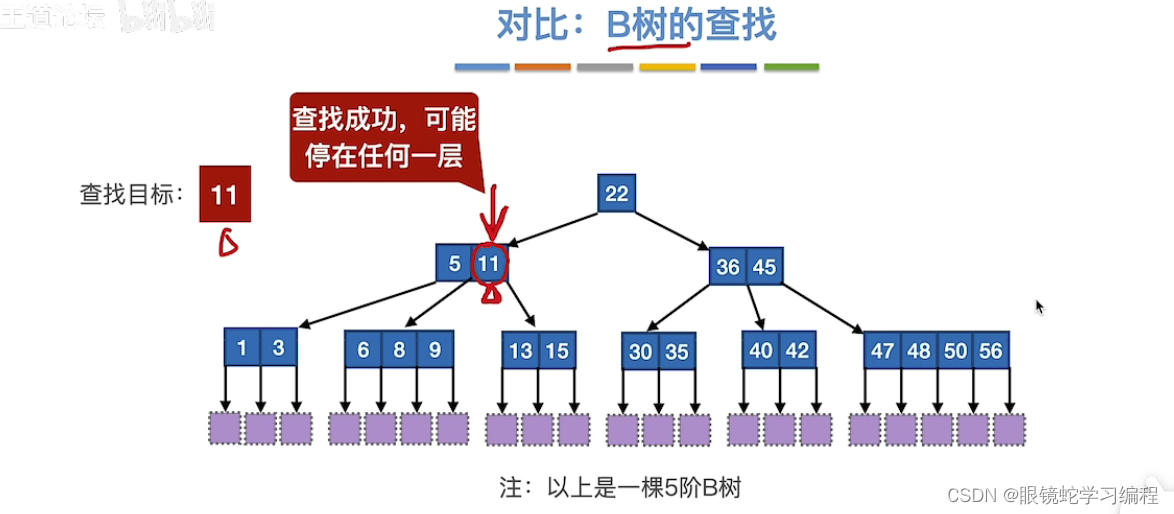
B+树与B树对比
