(一)发行版:Ubuntu16.04.7
(二)记录:
(1)
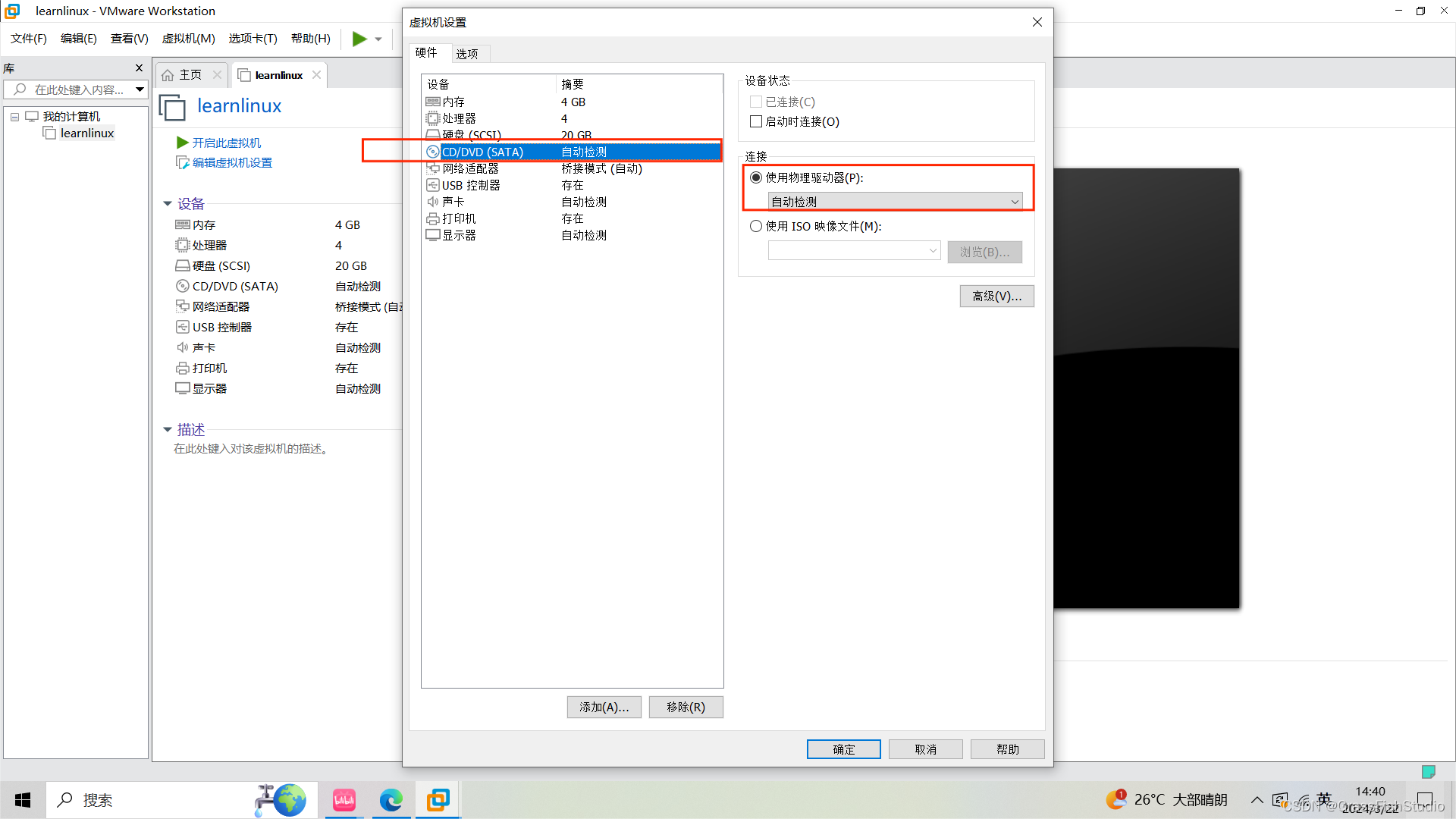
(2)打开虚拟机然后安装,出现灰色可能是已经安装过但是自己没有找到
 (3)删除VMwareTools命令(root权限)
(3)删除VMwareTools命令(root权限)
apt-get autoremove open-vm-tools(4)安装VMwareTools命令(root权限)
apt-get install open-vm-tools-desktop(5)要么按(2)安装要么按(4)安装
(6)安装后出现如下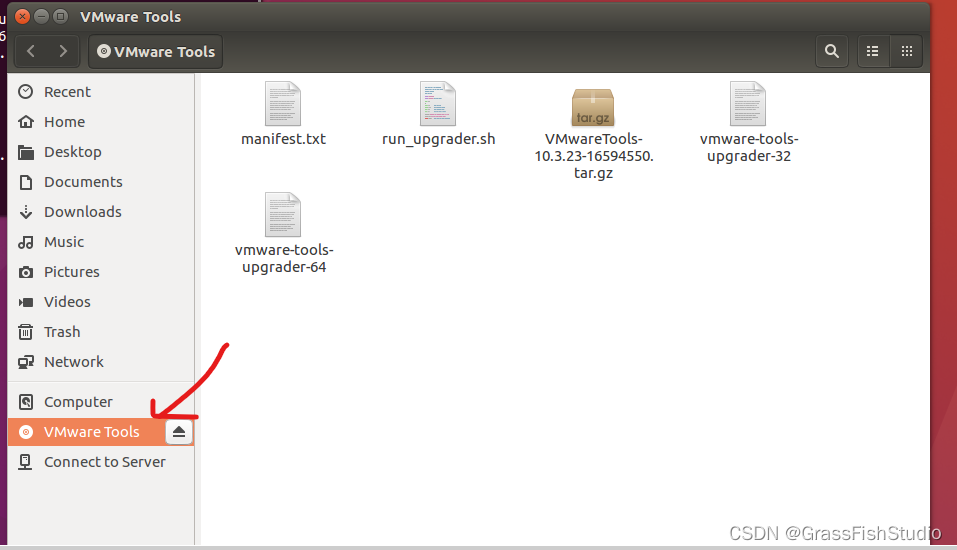 (7)
(7)
 (8)根目录下的opt目录用于存放第三方文件,所以我们把VMwareTool安装到该目录下
(8)根目录下的opt目录用于存放第三方文件,所以我们把VMwareTool安装到该目录下
a.创建一个文件夹(root权限)
mkdir /opt/vmtoolb.将压缩包解压缩到创建的文件夹中(版本号注意)
tar -vxf VMwareTools-10.3.23-16594550.tar.gz -C /opt/vmtool/ (9)查看解压生成的文件
(9)查看解压生成的文件

(10)找到可执行文件运行安装

(11)控制台键入reboot重启
(三)命令:
上述安装遇到一些问题
介绍另一种简单粗暴的安装方式(纯命令)
apt-get autoremove open-vm-toolsapt-get install open-vm-toolsapt-get install open-vm-tools-desktop测试:
在命令终端右键copy任意内容复制,粘贴到windows中