1.背景
1.1+0.1 = 1.2000000000000002
发现上面计算的值竟然和数学计算不一致
2. 问题
计算机是通过二进制计算的,如果我们在二进制的视角来看待上面问题,就很容易发现问题了。
例如:把「0.1」转成二进制的表示,然后还原成十进制,就能看出问题。
3. 0.1转二进制
小数转二进制,是通过除法进行的
0.1 = 1 ÷ 10
很简单,二进制就是要算
1 ÷ 1010
最终0.1转二进制是:0.0001100110011001100110011001100110011001100110011001101
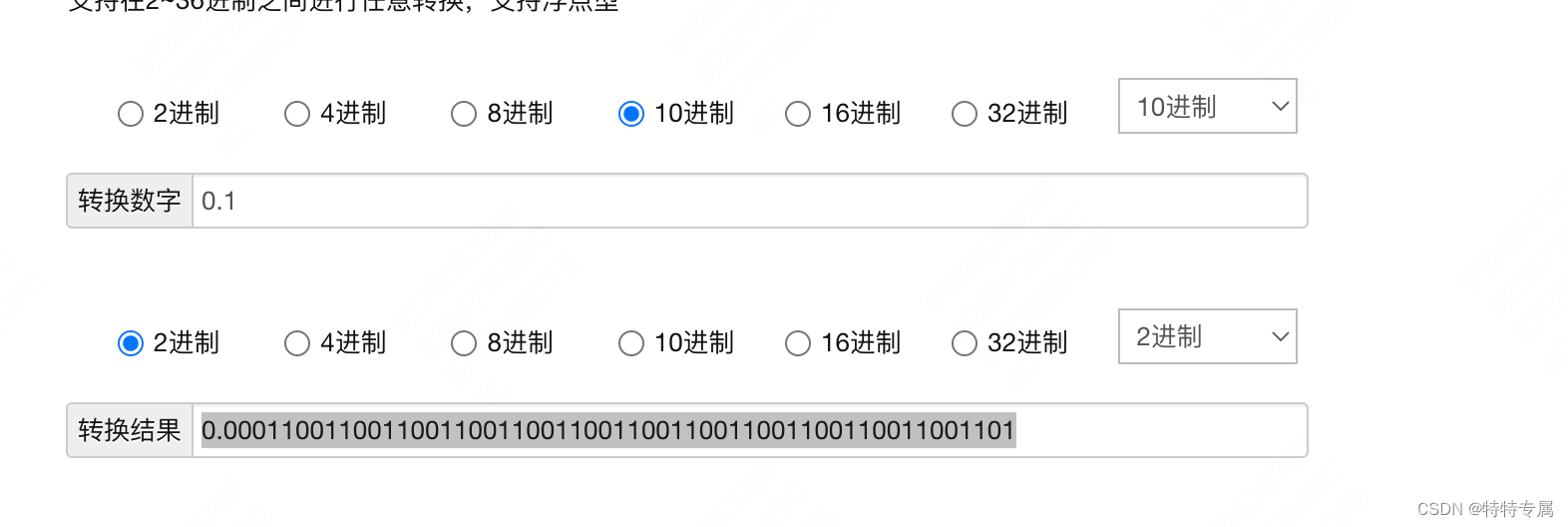
4.转换成对应精度数值
float的精度为7~8位有效数字,7位肯定能保证,8位的值也存在。
double的精度为16~17位有效数字
所以
二进制展示
1.1+0.1 = 1.0011001100110011001100110011001100110011001100110100
十进制展示
1.1+0.1 = 1.2000000000000002
5.解决方案
针对浮点数丢失精度的问题,我们可以通过BigDecimal来解决
new BigDecimal(double val)
该方法是不可预测的,以0.1为例,你以为你传了一个double类型的0.1,最后会返回一个值为0.1的BigDecimal吗?不会的,原因在于,0.1无法用有限长度的二进制数表示,无法精确地表示为双精度数,最后的结果会是0.100000xxx。
new BigDecimal(String val)
该方法是完全可预测的,也就是说你传入一个字符串"0.1",他就会给你返回一个值完全为0,1的BigDecimal,官方也表示,能用这个构造函数就用这个构造函数叭。
BigDecimal.valueOf(double val)
第二种构造方式已经足够优秀,可你还是想传入一个double值,怎么办呢?官方其实提供给你思路并且实现了它,可以使用Double.toString(double val)先将double值转为String,再调用第二种构造方式,你可以直接使用静态方法:valueOf(double val)。
总结:将double转为BigDecimal的时候,需要先把double转换为字符串,然后再作为BigDecimal(String val)构造函数的参数,这样才能避免出现精度问题。