34 机器学习（二）：数据准备|knn

文章目录

数据准备
- 数据下载
- 数据切割
- 转换器
- 估计器
kNN
- 正常的流程
- 网格+多折交叉训练
- 原理讲解
- 距离度量
- - 欧式距离(Euclidean Distance)
  - 曼哈顿距离(Manhattan Distance)
  - 切比雪夫距离 (Chebyshev Distance)
  - 还有一些自定义的距离就请读者自行研究
- 再识K-近邻算法API
- 选择n邻居的思辨
- 总结

数据准备

数据下载

首先我们需要了解的是：我们并不是把所有的数据都拿来训练，我们需要拿一部分当作训练集，一部分当作测试集，这也是最为基础的训练方式，现在实际上还有多折训练方式，这个上一讲有讲解过。

一般来说我们正常的训练方式下，我们把总共的数据分为训练集：测试集大概是7：3到8：2之间，都可以，并没有严格的说好坏，当数据量很大的时候，比如上亿了，甚至也可以9.9：0.1，毕竟数据量很大，这并没有严格的定义，与数据准备，我们采用sklearn当中的数据集进行学习。

先准备三个数据集，后面的介绍当中需要用到：

第一个数据集：鸢尾花数据集完成分类

from sklearn.datasets import load_iris# 鸢尾花数据集，用来完成分类的数据集 注意这个是load，load是临时加载，也就是这个数据集的大小很小，他会去网上下载了，直接放到内存，而不是放到你的具体的某一个磁盘的文件夹下，所以每一次开关编译器都需要重新进行加载 与下面的新闻数据集进行相对比
iris = load_iris()# 查看数据集的基本信息 一般第一次运行的时候可以查看一下 这边注释掉的原因是字太多占位置，读者第一次阅读的话可以打开
# print(iris_data.DESCR)# 获取特征值 一般对于深度学习和机器学习来说，我们都不会去关注data，我们会去关注他的shape,想看的可以打开。 iris_data.data是numpy类型的数据 这个也就是iris数据集的特征值
# print(iris_data.data)
print(iris.data.shape,end='\n\n')# 目标值
print(iris.target)
print('-'*20)# data当中的每一个特征代表什么，我们可以看到我们的特征值是150*4的也就是有150条数据，然后每一个数据有4个特征。
print(iris.feature_names,end='\n\n')  # 目标值的数字对应的含义，由于鸢尾花数据集是完成分类的，所以有target_names，如果是完成回归任务的，就没有target_names
print(iris.target_names)

输出：

(150, 4)[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 00 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 11 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 22 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 22 2]
--------------------
['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)']['setosa' 'versicolor' 'virginica']

第二个数据集：20类新闻的数据集注意fetch和load的区别

from sklearn.datasets import fetch_20newsgroups# 下面是比较大的数据，需要下载一会，20类新闻,他会下载到你的具体的文件夹下 明显也是分类问题
news = fetch_20newsgroups(subset='all', data_home='./dataset')
# 注释掉不看，读者可以自己看
# print(news.DESCR)# 分片看第一封信 也就是第一个数据的特征值
print(news.data[0])# 看第一封信的目标值 也就是第一个数据的目标值
print(news.target[0])
print('-'*20)# 一般来说的正常分析 看shape 看有多少条数据，以及特征数量
print(news.target)
print(min(news.target),max(news.target))# 因为输入的是文本，是一维的数据，所以没有特征name
# print(news.feature_names)

输出：

From: Mamatha Devineni Ratnam <mr47+@andrew.cmu.edu>
Subject: Pens fans reactions
Organization: Post Office, Carnegie Mellon, Pittsburgh, PA
Lines: 12
NNTP-Posting-Host: po4.andrew.cmu.eduI am sure some bashers of Pens fans are pretty confused about the lack
of any kind of posts about the recent Pens massacre of the Devils. Actually,
I am  bit puzzled too and a bit relieved. However, I am going to put an end
to non-PIttsburghers' relief with a bit of praise for the Pens. Man, they
are killing those Devils worse than I thought. Jagr just showed you why
he is much better than his regular season stats. He is also a lot
fo fun to watch in the playoffs. Bowman should let JAgr have a lot of
fun in the next couple of games since the Pens are going to beat the pulp out of Jersey anyway. I was very disappointed not to see the Islanders lose the final
regular season game.          PENS RULE!!!10
--------------------
[10  3 17 ...  3  1  7]
0 19

第三个数据集：波士顿房价的数据集这个用来做回归的：

from sklearn.datasets import load_boston
# 接着来看回归的数据,是波士顿房价 原本的方式，1.2之后需要换方式下载
money= load_boston()# 一样不看这个
# print(money.DESCR)# 看一下数据集的特征值的基本属性
print(money.data[0])
print(money.data.shape)
print(money.feature_names)
print('-' * 20)# 看一下数据集的目标值的基本属性
# 回归问题没这个,打印这个会报错
# print(lb.target_names)
print(money.target)

输出：

# 这边给出上面的输出：
# [6.320e-03 1.800e+01 2.310e+00 0.000e+00 5.380e-01 6.575e+00 6.520e+01
#  4.090e+00 1.000e+00 2.960e+02 1.530e+01 3.969e+02 4.980e+00]
# (506, 13)
# ['CRIM' 'ZN' 'INDUS' 'CHAS' 'NOX' 'RM' 'AGE' 'DIS' 'RAD' 'TAX' 'PTRATIO'
#  'B' 'LSTAT']
# --------------------------------------------------
# [24.  ···一堆数据 11.9]

数据切割

from sklearn.model_selection import train_test_split# 这里跳到去运行第一个下载数据的代码
# 下载的代码 阿巴阿巴# 注意返回值, 训练集:x_train,y_train 测试集：x_test,y_test，顺序千万别搞错了
# test_size=0.25 就是训练集：测试集=3：1
# 默认是乱序的,random_state为了确保两次的随机策略一致，往往会带上
x_train, x_test, y_train, y_test = train_test_split(iris.data, iris.target, test_size=0.25, random_state=1)print("训练集特征值shape", x_train.shape)
print("测试集特征值shape", x_test.shape)

输出：

训练集特征值shape (112, 4)
测试集特征值shape (38, 4)

转换器

Transformer是给测试集用的
fit_transform(对于文档建立分类词频矩阵，不能同时调用)给训练集用的

什么意思呢？实际上这两个是一样的，我们训练集的使用肯定在测试集之前，我们先fit_transform之后再对于测试集要再进行一次fit？明显不合理，因为fit的过程实际上会对训练集进行切割，分组得到一些参数，那我们在测试的时候应该做的是调用那些参数去执行，得到预测的目标值，然后和真正的目标值进行比较，最后对模型进行评估。

先记忆，后面写代码的时候会有更深的印象。

估计器

在 sklearn 中，估计器(estimator)是一个重要的角色，分类器和回归器都属于
estimator，是一类实现了算法的 API，先记忆，后面写代码的时候会有更深的印象

kNN

先讲解使用，再讲解算法，我个人会觉得这样子更好理解

正常的流程

# K近邻
from sklearn.preprocessing import StandardScaler
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import train_test_split
# 读取数据
data = pd.read_csv("./dataset/data1_facebook/train.csv")
# 别从直接window打开
print(data.head(3))
print(data.shape)# 处理数据
# 1、缩小数据,查询数据,为了减少计算时间，实际不会这么操作，学习上使用，减少数据量，避免跑太久，毕竟快3000万的数据集
data = data.query("x > 1.0 &  x < 1.05 & y > 2.5 & y < 2.55")# 处理时间的数据 返回一个Series
time_value = pd.to_datetime(data['time'], unit='s')
print(time_value.iloc[0])  #最大时间是1月10号
print('-' * 20)# 把日期格式转换成 字典格式，把年，月，日，时，分，秒转换为字典格式，
time_value = pd.DatetimeIndex(time_value)# 构造一些特征，执行的警告是因为我们的操作是复制，loc是直接放入
# 日期，是否是周末，小时对于个人行为的影响是较大的
data.insert(data.shape[1], 'day', time_value.day)
data.insert(data.shape[1], 'hour', time_value.hour)
data.insert(data.shape[1], 'weekday', time_value.weekday)
print(data.head(3))
print('-' * 20)# 把时间戳特征删除
data = data.drop(['time'], axis=1)# 把签到数量少于n个目标位置删除
place_count = data.groupby('place_id').count()
# 把index变为0,1,2，3,4,5,6这种效果，从零开始拍，原来的index是地点
# 只选择去的人大于3的数据，认为1,2,3的是噪音
tf = place_count[place_count.row_id > 5].reset_index()
print(tf.head(3))
print('-' * 20)# 根据设定的地点目标值，对原本的样本进行过滤
data = data[data['place_id'].isin(tf.place_id)]
print(data.head(3))
print('-'*20)# 取出数据当中的特征值和目标值
y = data['place_id']
x = data.drop(['place_id'], axis=1)
x = x.drop(['row_id'], axis=1)
print(x.shape)
print(x.columns)
print('-'*20)# 进行数据的分割训练集合测试集
# random_state 随机数种子,不同的种子会造成不同的随机采样结果。相同的种子采样结果相同。
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.25, random_state=1)# 特征工程（标准化）,下面3行注释，一开始我们不进行标准化，看下效果，目标值要不要标准化？
std = StandardScaler()# 对测试集和训练集的特征值进行标准化,服务于knn fit
# transfrom不再进行均值和方差的计算，是在原有的基础上去标准化
x_train = std.fit_transform(x_train)
x_test = std.transform(x_test)
print(x_train.shape)
print(x_test.shape)# 进行算法流程 可以通过调整超参数n_neighbors=5，来调整结果好坏
knn = KNeighborsClassifier(n_neighbors=5)# fit， predict,score，训练,参数是放在knn的内部的参数当中
knn.fit(x_train, y_train)# 得出预测结果
y_predict = knn.predict(x_test)
print("预测的目标签到位置为：", y_predict)
print("预测的准确率:", knn.score(x_test, y_test))

输出：

   row_id       x       y  accuracy    time    place_id
0       0  0.7941  9.0809        54  470702  8523065625
1       1  5.9567  4.7968        13  186555  1757726713
2       2  8.3078  7.0407        74  322648  1137537235
(29118021, 6)
1970-01-09 15:26:06
--------------------row_id       x       y  accuracy    time    place_id  day  hour  \
7468      7468  1.0058  2.5096        66  746766  9076695703    9    15   
44694    44694  1.0380  2.5315       152  657007  5035268417    8    14   
215164  215164  1.0274  2.5317        65  154944  6399991653    2    19   weekday  
7468          4  
44694         3  
215164        4  
--------------------place_id  row_id   x   y  accuracy  day  hour  weekday
0  1228935308      27  27  27        27   27    27       27
1  2212762406       6   6   6         6    6     6        6
2  2584530303      78  78  78        78   78    78       78
--------------------row_id       x       y  accuracy    place_id  day  hour  weekday
44694    44694  1.0380  2.5315       152  5035268417    8    14        3
215164  215164  1.0274  2.5317        65  6399991653    2    19        4
276048  276048  1.0235  2.5320        24  1228935308    6    12        1
--------------------
(671, 6)
Index(['x', 'y', 'accuracy', 'day', 'hour', 'weekday'], dtype='object')
--------------------
(503, 6)
(168, 6)
预测的目标签到位置为： [2584530303 ············· 102186]
预测的准确率: 0.39285714285714285

网格+多折交叉训练

# 采用网格搜索进行训练knn 实际上就是排列组合
from sklearn.preprocessing import StandardScaler
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import train_test_split,GridSearchCV# 先进行数据处理 和之前的步骤一样，这边就不进行详细介绍，我把那些print全部去掉
# --------------------------------------------------------------
data = pd.read_csv("./dataset/data1_facebook/train.csv")
data = data.query("x > 1.0 &  x < 1.05 & y > 2.5 & y < 2.55")
time_value = pd.to_datetime(data['time'], unit='s')
time_value = pd.DatetimeIndex(time_value)
data.insert(data.shape[1], 'day', time_value.day)
data.insert(data.shape[1], 'hour', time_value.hour)
data.insert(data.shape[1], 'weekday', time_value.weekday)
data = data.drop(['time'], axis=1)
place_count = data.groupby('place_id').count()
tf = place_count[place_count.row_id > 5].reset_index()
data = data[data['place_id'].isin(tf.place_id)]
y = data['place_id']
x = data.drop(['place_id'], axis=1)
x = x.drop(['row_id'], axis=1)# 这一步虽然一样，但是由于后面涉及到多折交叉，这边就需要读者了解一下训练集 测试集 验证集
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.25, random_state=1)std = StandardScaler()
x_train = std.fit_transform(x_train)
x_test = std.transform(x_test)
# ------------------------------------------------------------# 这个是kNN我们要传进去的参数
param = {"n_neighbors": [3, 5, 10, 12, 15]}# 参数n_neighbors可写可不写
knn = KNeighborsClassifier()# 进行网格搜索，cv=3是3折交叉验证，用其中2折训练，1折验证
gc = GridSearchCV(knn, param_grid=param, cv=3)#你给它的x_train，它实际上会自己分成训练集和验证集，用于评估他自己的正确率，所以最后训练出来的会比我们上面的来的大概率垃圾一点，原因就是训练量太小了。
gc.fit(x_train, y_train)# 预测准确率，为了给大家看看
print("在测试集上准确率：", gc.score(x_test, y_test))
print("在交叉验证当中最好的结果：", gc.best_score_)
print("选择最好的模型是：", gc.best_estimator_)
print("每个超参数每次交叉验证的结果：", gc.cv_results_)

输出：

在测试集上准确率： 0.3869047619047619
在交叉验证当中最好的结果： 0.48719228210246174
选择最好的模型是： KNeighborsClassifier(n_neighbors=10)
每个超参数每次交叉验证的结果： {'mean_fit_time': array([0.00345572, 0.        , 0.        , 0.00148535, 0.        ]), 'std_fit_time': array([0.00488712, 0.        , 0.        , 0.00114506, 0.        ]), 'mean_score_time': array([0.01625578, 0.01041603, 0.01131908, 0.00851194, 0.01728145]), 'std_score_time': array([0.00531625, 0.00736525, 0.00800519, 0.00618463, 0.0062666 ]), 'param_n_neighbors': masked_array(data=[3, 5, 10, 12, 15],mask=[False, False, False, False, False],fill_value='?',dtype=object), 'params': [{'n_neighbors': 3}, {'n_neighbors': 5}, {'n_neighbors': 10}, {'n_neighbors': 12}, {'n_neighbors': 15}], 'split0_test_score': array([0.38690476, 0.44047619, 0.48214286, 0.43452381, 0.44047619]), 'split1_test_score': array([0.35714286, 0.44047619, 0.43452381, 0.44047619, 0.44642857]), 'split2_test_score': array([0.47305389, 0.48502994, 0.54491018, 0.53892216, 0.52694611]), 'mean_test_score': array([0.4057005 , 0.45532744, 0.48719228, 0.47130739, 0.47128362]), 'std_test_score': array([0.04915148, 0.02100284, 0.04520627, 0.04787258, 0.03943426]), 'rank_test_score': array([5, 4, 1, 2, 3])}

原理讲解

最近邻 (k-Nearest Neighbors，KNN) 算法是一种分类算法，该算法的思想是：一个样本与数据集中的k个样本最相似，如果这k个样本中的大多数属于某一个类别。

实现流程：
1）计算已知类别数据集中的点与当前点之间的距离
2）按距离递增次序排序
3）选取与当前点距离最小的k个点
4）统计前k个点所在的类别出现的频率
5）返回前k个点出现频率最高的类别作为当前点的预测分类

距离度量

这边的距离度量再sklearn当中采用的是欧氏距离，但常用的距离还有很多种，这就需要我们通过自己的经验去分析与使用。

默认包含的一般有：

欧式距离
曼哈顿距离（‘manhattan’）
切比雪夫距离（‘chebyshev’）
闵可夫斯基距离（‘minkowski’）

欧式距离(Euclidean Distance)

默认采用的就是欧式距离，这个大家也很了解，两点之间直线最短是吧。。。

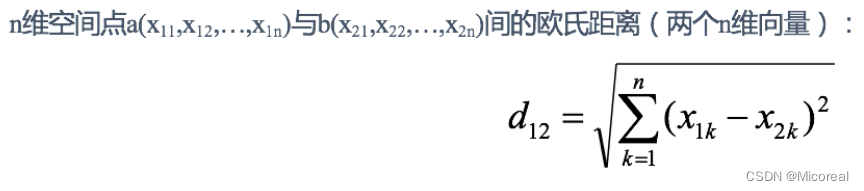
在这里插入图片描述
使用欧式距离的话实际上,不需要指定metric参数，默认使用的就是欧氏距离。

曼哈顿距离(Manhattan Distance)

在曼哈顿街区要从一个十字路口开车到另一个十字路口，驾驶距离显然不是两点间的直线距离。这个实际驾驶距离就是“曼哈顿距离”。曼哈顿距离也称为“城市街区距离”(City Block distance)。

关键字：manhattan
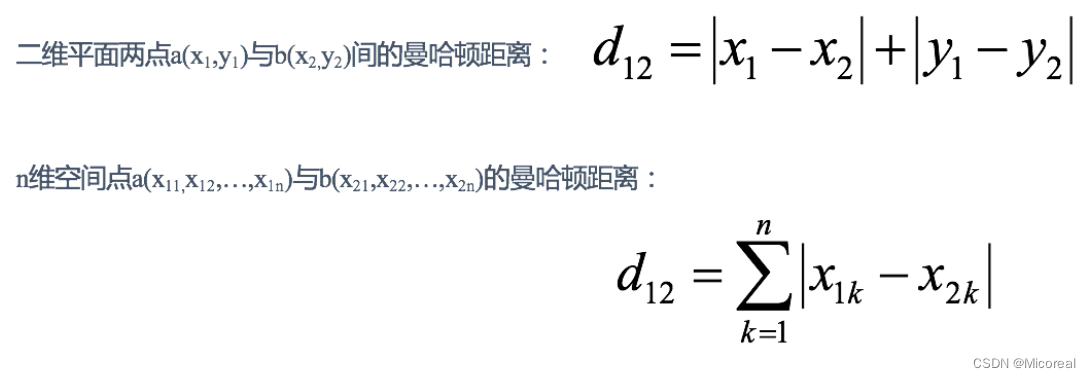
在这里插入图片描述
使用的话：

knn = KNeighborsClassifier(n_neighbors=5,metric='manhattan')

如果我们上面的代码进行修改使用曼哈顿进行训练的话，实际上会效果更好。

切比雪夫距离 (Chebyshev Distance)

国际象棋中，国王可以直行、横行、斜行，所以国王走一步可以移动到相邻8个方格中的任意一个。国王从格子(x1,y1)走到格子(x2,y2)最少需要多少步？这个距离就叫切比雪夫距离，实际上就是比曼哈顿距离多了个斜行。

在这里插入图片描述

还有一些自定义的距离就请读者自行研究

再识K-近邻算法API

sklearn.neighbors.KNeighborsClassifier(n_neighbors=5,algorithm=‘auto’)

n_neighbors：int,可选（默认= 5)
algorithm：{‘auto’，‘ball_tree’，‘kd_tree’，‘brute’}
快速k近邻搜索算法，默认参数为auto，可以理解为算法自己决定合适的搜索算法。除此之外，用户也可以自己指定搜索算法ball_tree、kd_tree、brute方法进行搜索，brute是蛮力搜索，也就是线性扫描，当训练集很大时，计算非常耗时。kd_tree，构造kd树存储数据以便对其进行快速检索的树形数据结构，kd树也就是数据结构中的二叉树。以中值切分构造的树，每个结点是一个超矩形，在维数小于20时效率高。ball tree是为了克服kd树高纬失效而发明的，其构造过程是以质心C和半径r分割样本空间，每个节点是一个超球体
metric 采用的距离的度量：默认欧氏距离，曼哈顿距离（‘manhattan’）切比雪夫距离（‘chebyshev’),闵可夫斯基距离（‘minkowski’）

选择n邻居的思辨

选择较小的 K 值，就相当于用较小的领域中的训练实例进行预测，“学习”近似误差会减小，只有与输入实例较近或相似的训练实例才会对预测结果起作用，与此同时带来的问题是“学习”的估计误差会增大，换句话说，K 值的减小就意味着整体模型变得复杂容易发生过拟合。

选择较大的 K 值，就相当于用较大领域中的训练实例进行预测，其优点是可以减少学习的估计误差，但缺点是学习的近似误差会增大。这时候，与输入实例较远（不相似的）训练实例也会对预测器作用，使预测发生错误，且== K 值的增大就意味着整体的模型变得简单==。
K=N（N 为训练样本个数），则完全不足取，因为此时无论输入实例是什么，都只是简单的预测它属于在训练实例中最多的类，模型过于简单，忽略了训练实例中大量有用信息。在实际应用中，K 值一般取一个比较小的数值，例如采用交叉验证法（简单来说，就是把训练数据在分成两组:训练集和验证集）来选择最优的 K 值。对这个简单的分类器进行泛化，用核方法把这个线性模型扩展到非线性的情况，具体方法是把低维数据集映射到高维特征空间。