半监督学习，一般应用于少量带标签的数据（数量R）和大量未带标签数据的场景（数量U），一般来说，U>>R。

半监督学习一般可以分为2种情况，一种是transductive learning，这种情况下，将unlabeled data的feature利用进来。另外一种是inductive learning，这种情况下，在训练的整个过程中，完全不看任何unlabeled data的信息。

为什么要做semi-supervised learning呢，因为我们现实中大多数情况下，搜集数据比较容易，但是数据标注比较困难。包括我们的人生中，我们自己也是一直在做semi-supervised learning.

为什么semi-supervised learning会有用呢，因为unlabeled data可以告诉我们一些信息。通常，我们在做semi-supervised learning时，会做出一些假设，这个假设很关键，会影响最后的结果。

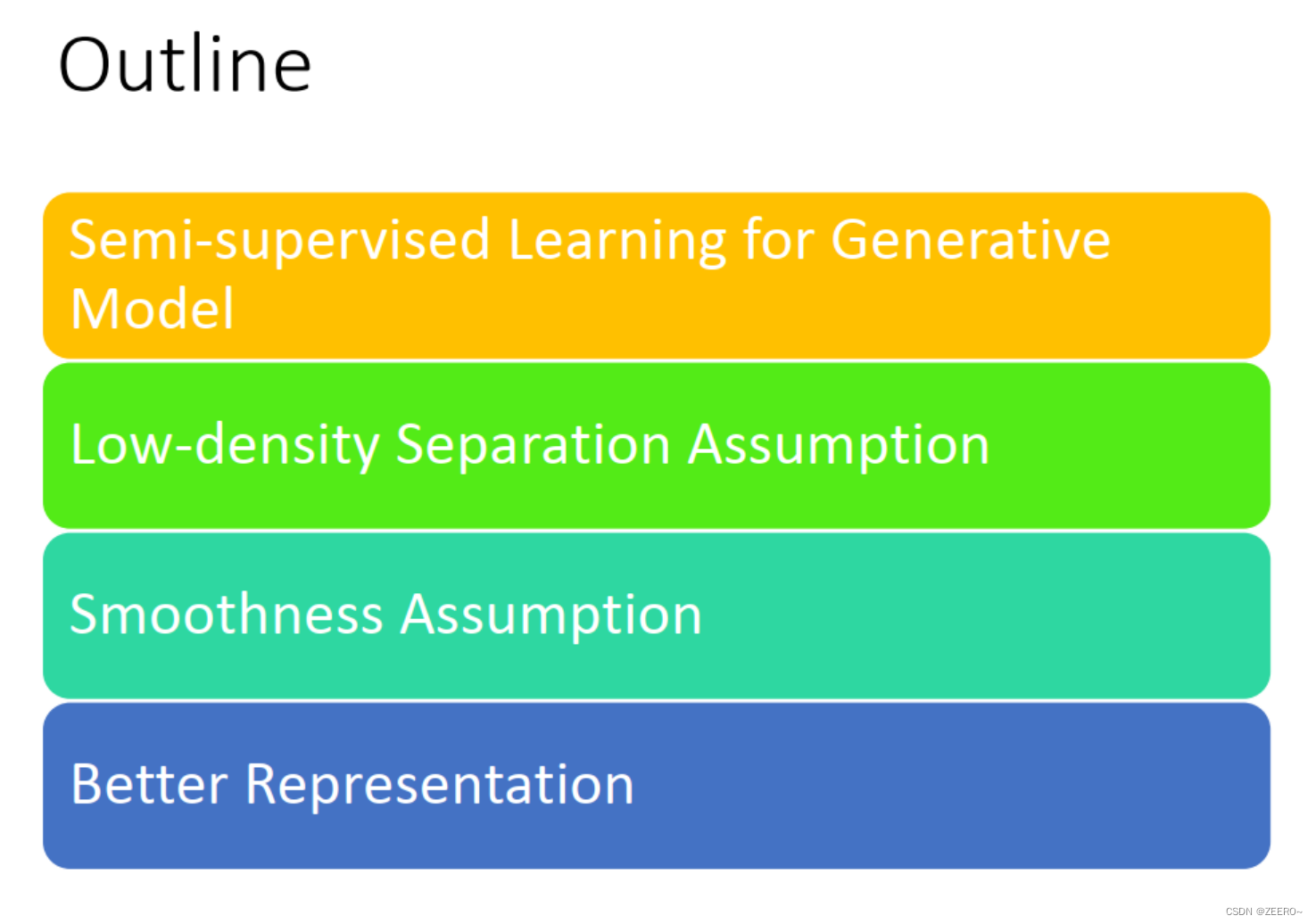
这节课的主要讲述4个部分，第一个是讲generative model时如何做semi-supervised learning。然后在讲述2个常用的通用假设，分别是low density separation假设和smoothness假设，最后，semi-supervised learning还有一个比较好用的一招是better representation。

1、Generative Model

假设说我们已知标签的数据，有两个类别C1和C2，假设他们是属于高斯分布。我们可以画出我们的决策边界，对于任何一个数据，可以求出这个数据x属于类别C1的概率，如上图所示。

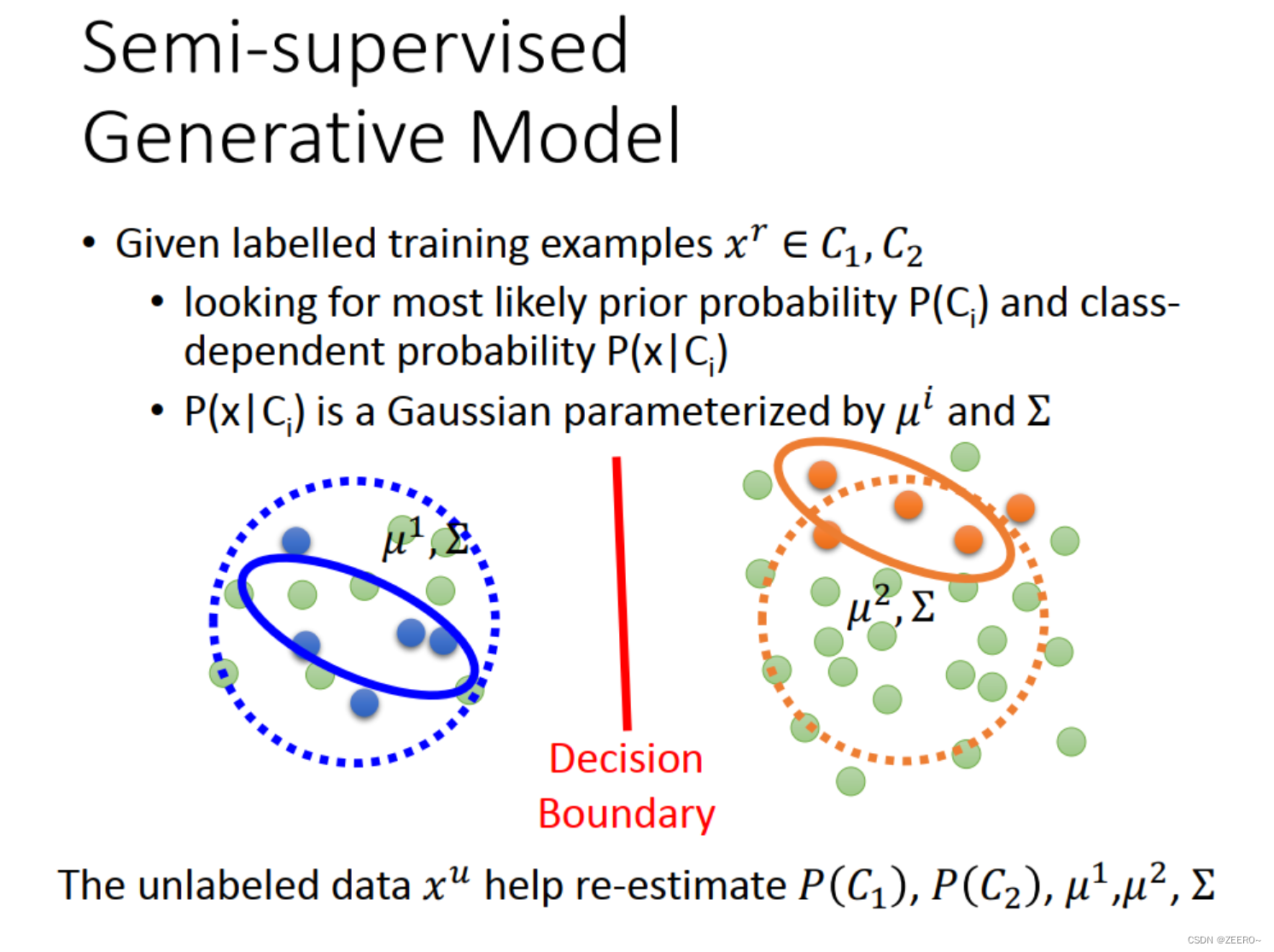
但是，这个时候如果再给了一个unlabeled data，那么我们上面的决策边界就会受到影响。这在直觉上是这样。

实际操作是怎么做的呢？
首先，先初始化一组参数$\theta$。初始化可以随机设定参数，虽然说初始化的值也很重要。
第一步， 根据初始设定的参数，可以估计每个unlabeled data属于class 1的概率。
第二步，算出第一步的概率之后，便可以update 我们的model。
后续不断重复第一步和第二步。
如果我们知道EM算法的话，那么第一步就是E的过程，第二步就是M的过程。

这件事情直觉上可以理解为何这样做，我们实际上还是分析下原因，如上图所示。

2、Low density Separation Assumption

我们认为这个世界是一个非黑即白的世界。意思就是，在两个类别的交界处，密度是比较低的，data量是很少的，基本上不太会出现data。Low density最具代表性的方法就是self training。

self training的方法非常的直觉和通俗易懂，我们不做过多的讲述。
我们现在需要来考虑的一个问题时，self training的方法如果用来做回归regression，会怎么样呢？work吗？
我们可以花5s的时间思考一下。
答案其实是无效的。拿最简单的线性回归为例，不断self training出来的数据，再加入到model中进行训练，model不会发生变化，因此这招对于regression是无效的。

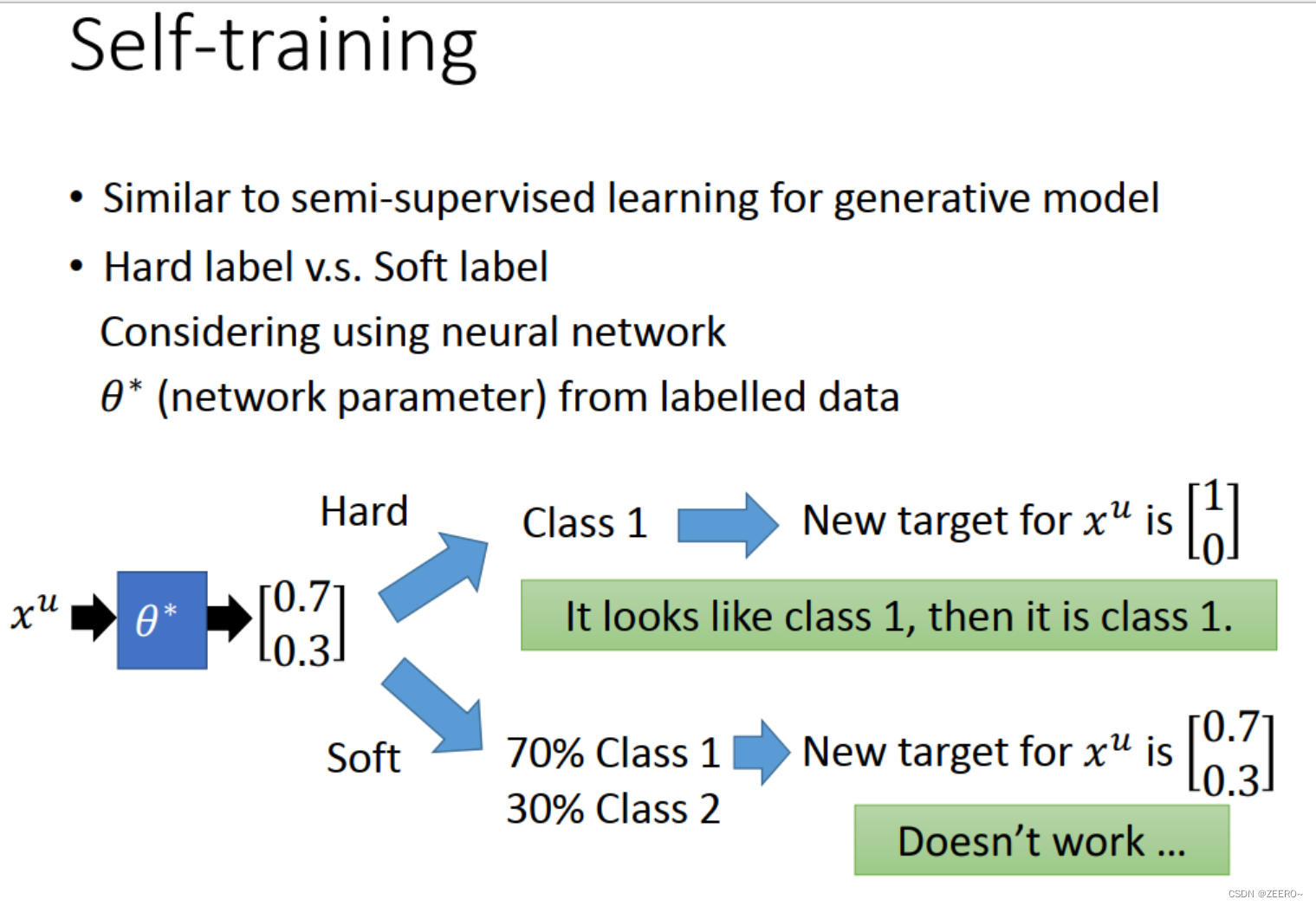
self training的过程和之前的generative model的过程还是非常相似的，但也有不同之处。主要的不同之处在于hard label和soft label的区别。以神经网络为例，我们可以想下hard label和soft label哪个有效？
实际上，如果以ANN为例，soft label是完全无效的。为什么呢？因为在现有的参数上这个unlabeled data都可以做到[0.7,0.3]的输出，如果此时标签还是[0.7,0.3]，那么就完全不需要更新参数了，不需要更新model了。

Entropy-based Regularization

熵要越小越好。可以在损失函数时将unlabeled data的熵一起加入作为最小化项。

3、Smoothness Assumption

Smoothness Assumption的基本思想是，如果x相似，那么具有相同的标签。更具体的来说，如果数据的分布并不平均，那么假如两个x之间数据流非常密集，那么两个x具有相同的标签。如上图所示，虽然x2与x3的距离更近，但是x1和x2具有相同的标签。
这种假设往往更符合真实假设，因为同一种类别之间会有非常多的过渡形态。

如何实现Smoothness Assumption

1 cluster and then label

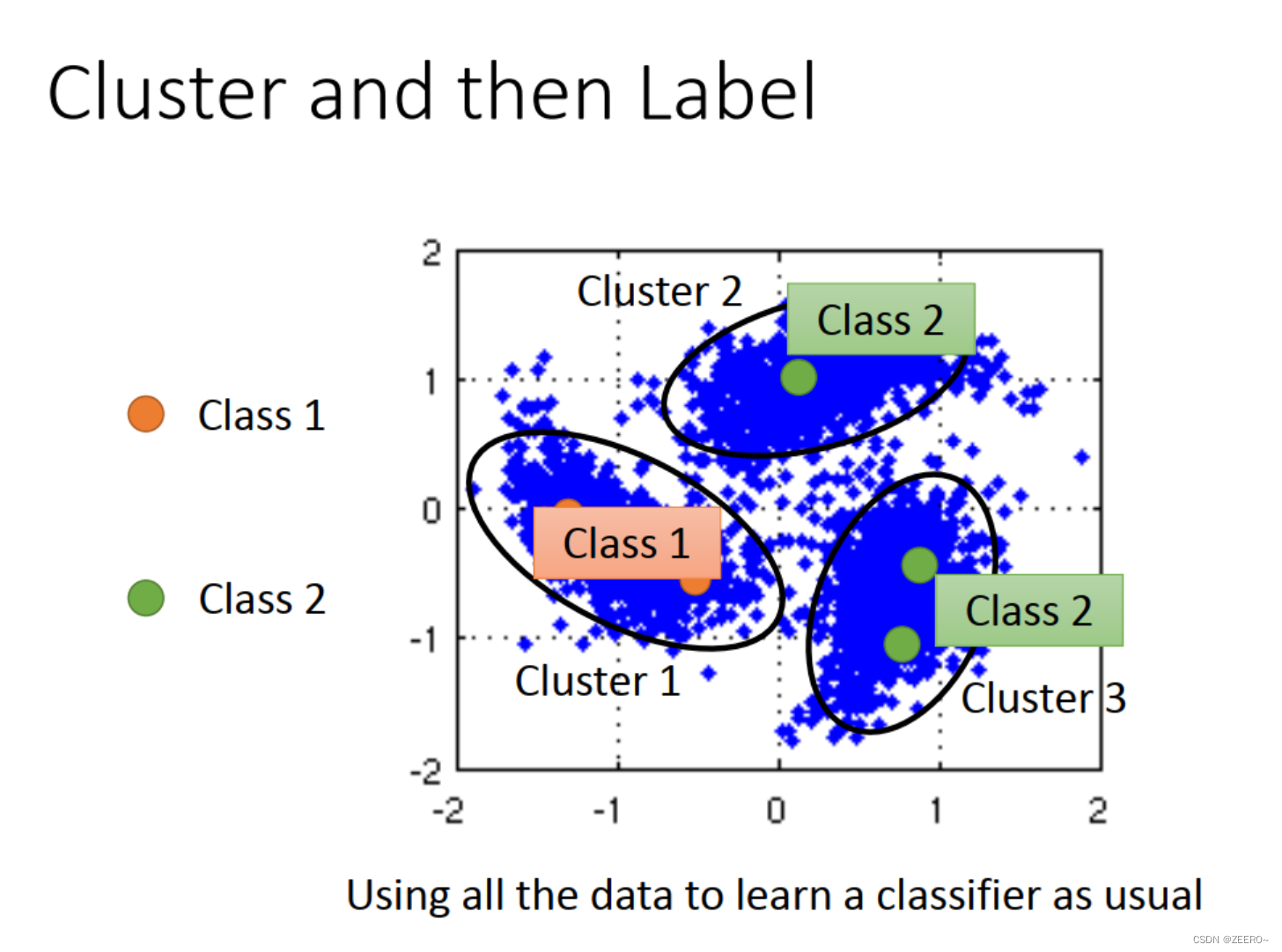
最简单的方法是聚类和打标。这个方法的前提假设是我们可以将同一个class的label都聚集在一起。但是，例如说在图像识别中，可能同一个class会长的很不像，不同的class会长的很像。因此，如果要使得这个方法有用，那么你的cluster的方法要很强。
在我们尝试的时候，可以用deep autoencoder来实现。
一般先用deep autoencoder进行call feature，然后再call clustering，这样一般就会work。

2 graph-based approach

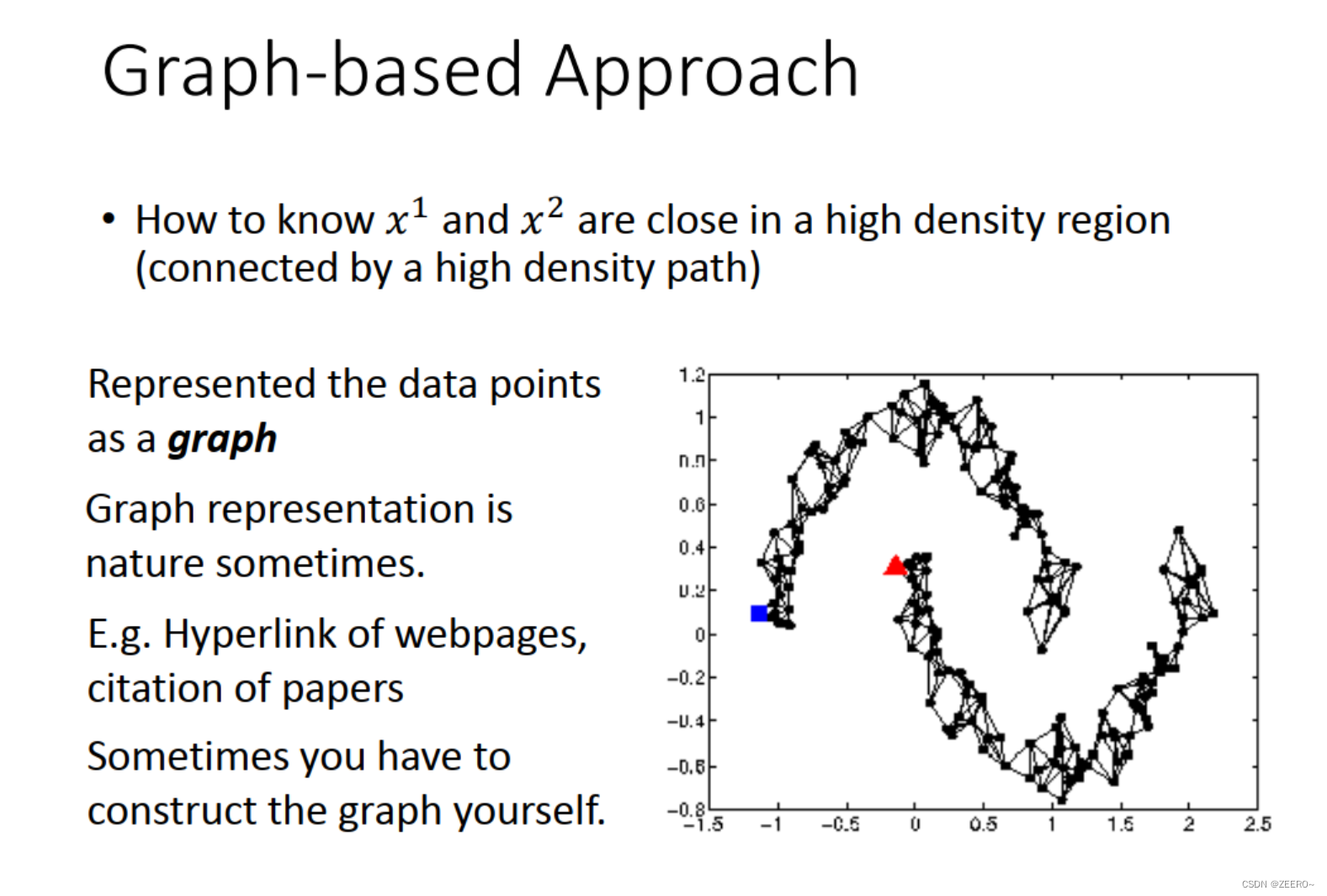
我们使用graph来表达connected by a high density path这件事情。我们把所有的data points都建立成一个graph。这样的话，如果有2个点，在graph上是相连的，是走的到的，那么他们就是同一个class.
有时候，建立这个graph是一件很自然的事情，但有时候，我们要自己想办法去建立这个graph。

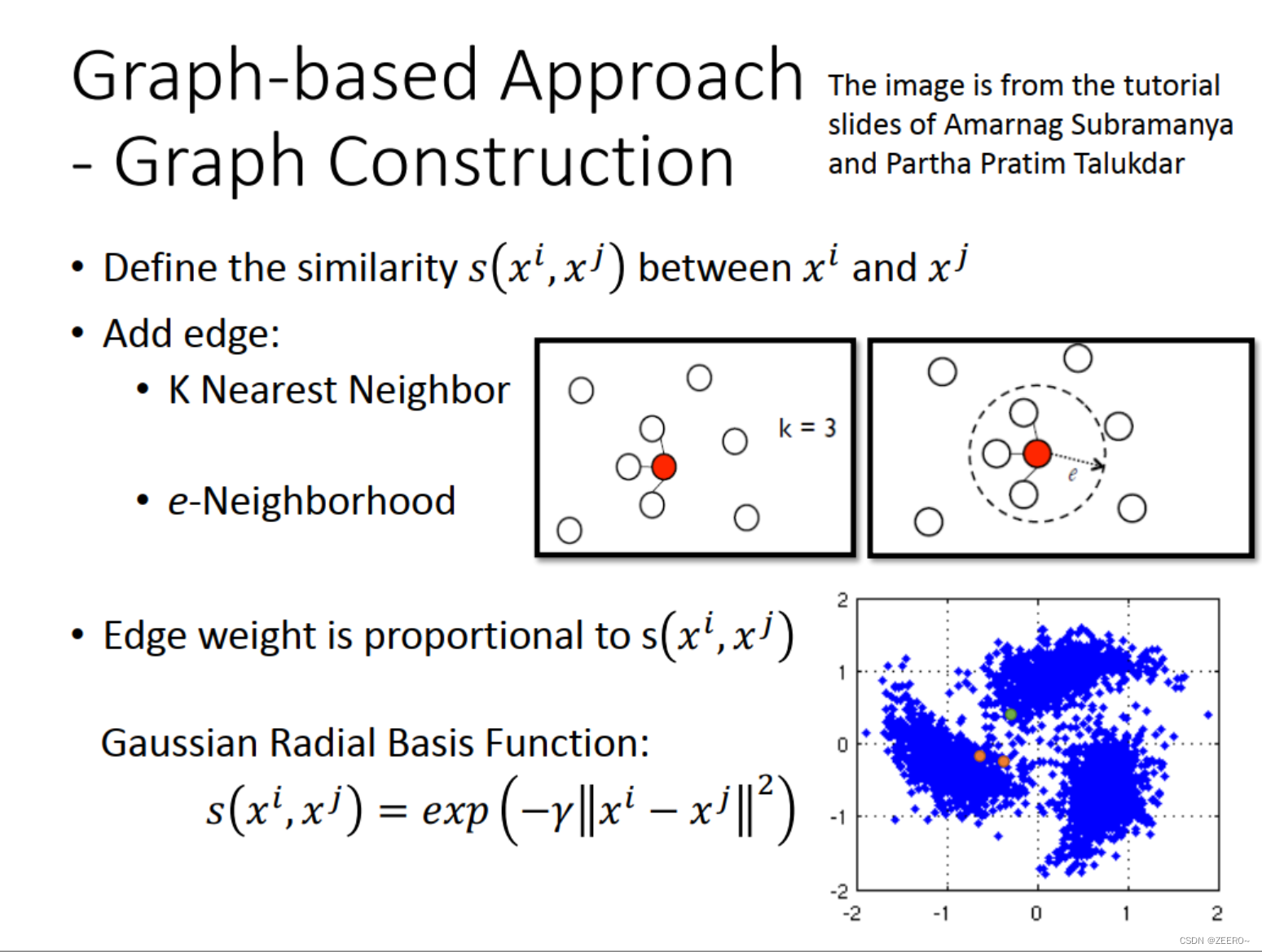
一个graph对结果的影响是非常重要的。但是这个事情做起来，很多的时候，凭的是自己的直觉。通常我们可以这样做：

首先需要定义如何去计算他们之间的相似度，例如说对于图像，直接从像素层面去建立相似度，可能效果会比较差。但是如果经过auto-encoder之后再建立相似度，结果可能会比较好。

算完相似度之后，我们便可以开始建立graph了。可以利用KNN的方法，相连固定k个值，也可以用e-neighborhood，只相连相似度超过一定阈值的点。也可以用RBF函数来计算相似度。使用RBF函数的优点在于，只要距离远一点点，那么相似度就下降非常快。

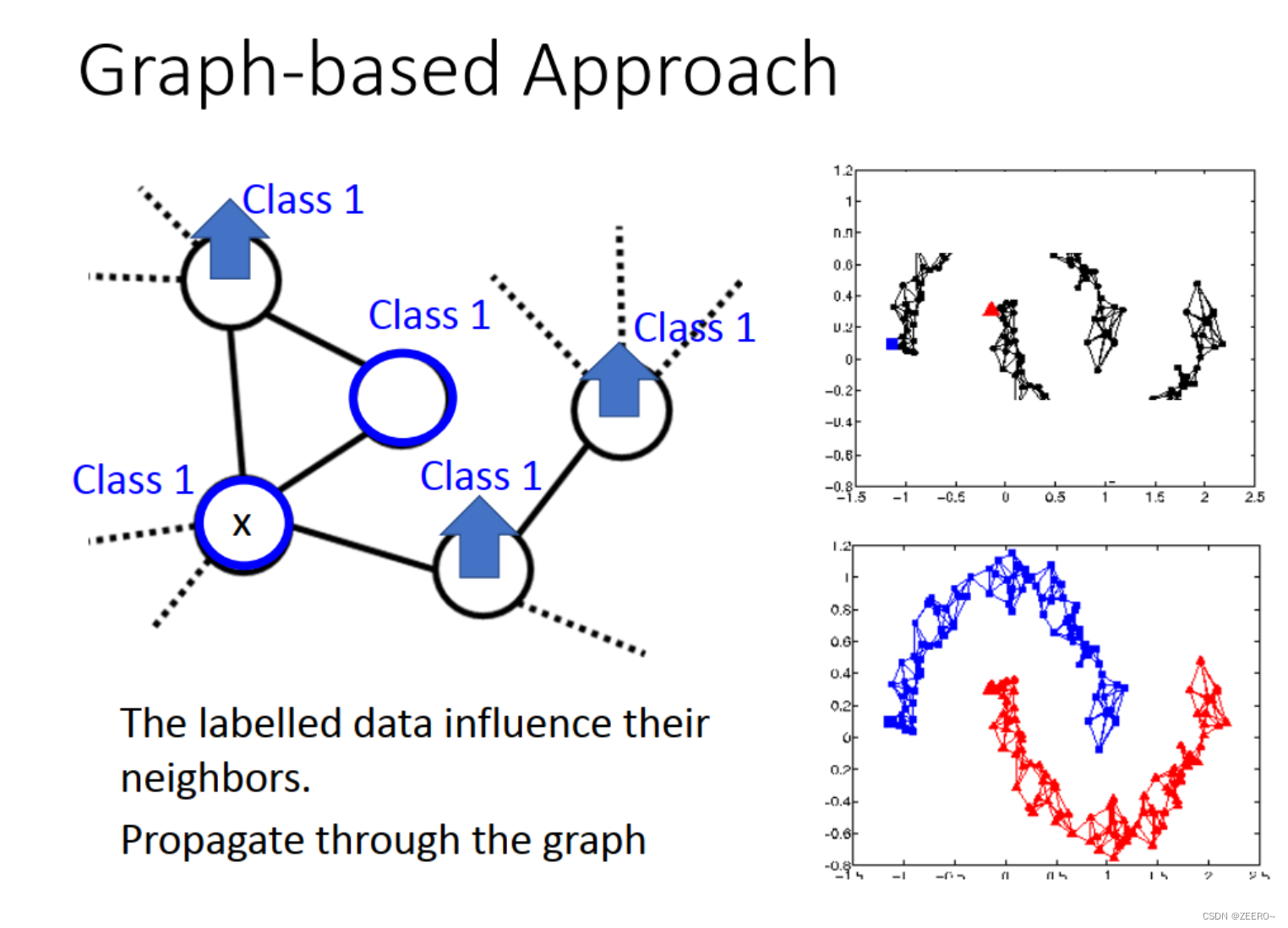
在这种机制下，类别会不断的传播。

之前算是定性地计算这种graph，接下来我们来定量地表示。
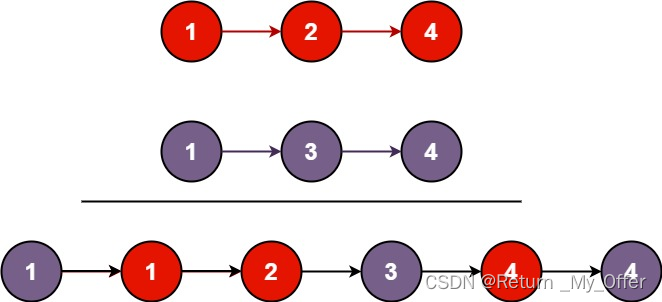
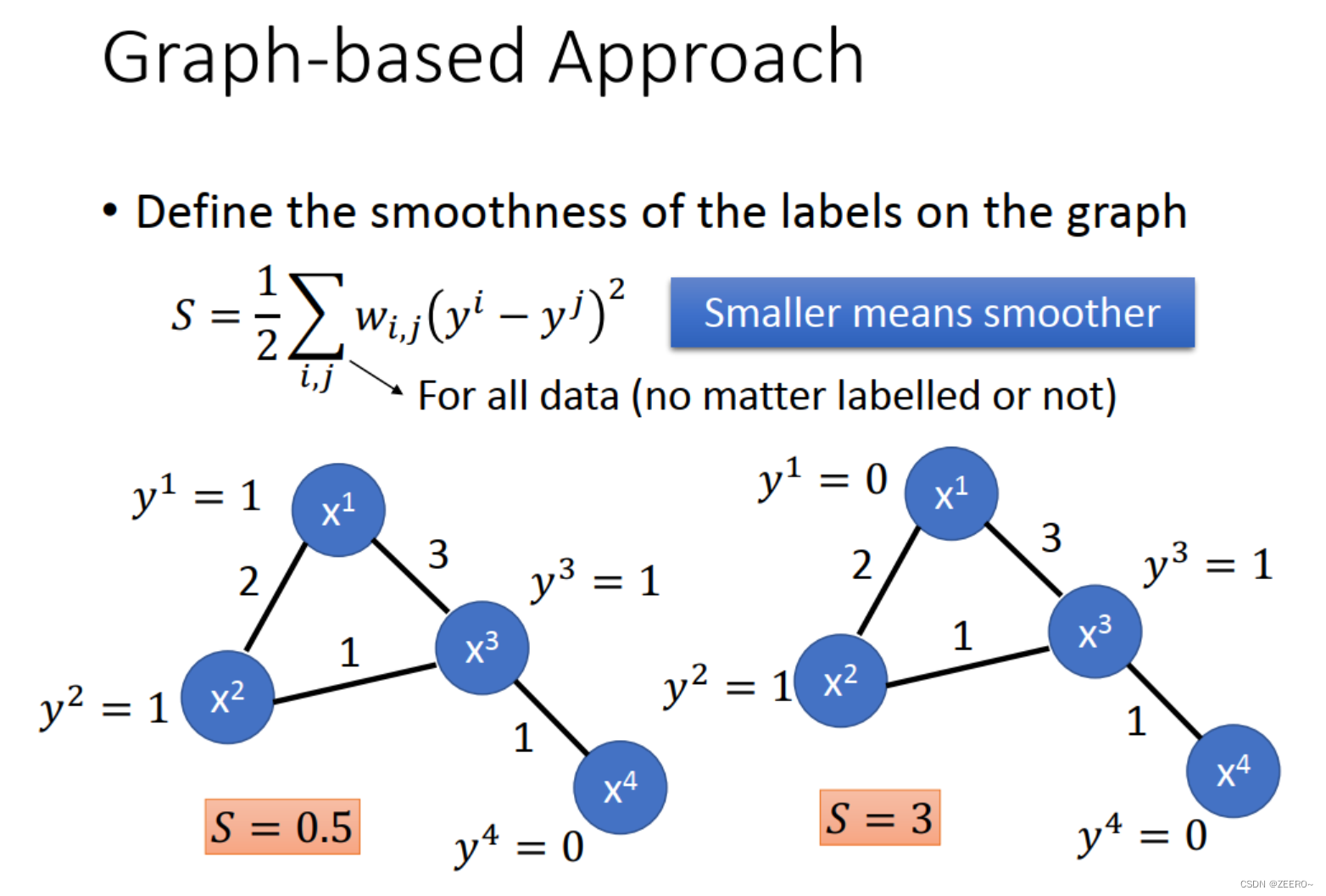
我们需要定义一个量，smoothness，例如说上图中存在2个例子，左右都有4个点，连线上的数字代表的是权重weight。现在我们来考虑下，左右两边哪边比较smooth一些。我们都会觉得左边更加smooth一些。我们可以用一个公式来定量的描述左右两边到底有多smooth。smooth程度用s表示，左边s=0.5，右边s=3。s值越小越好。

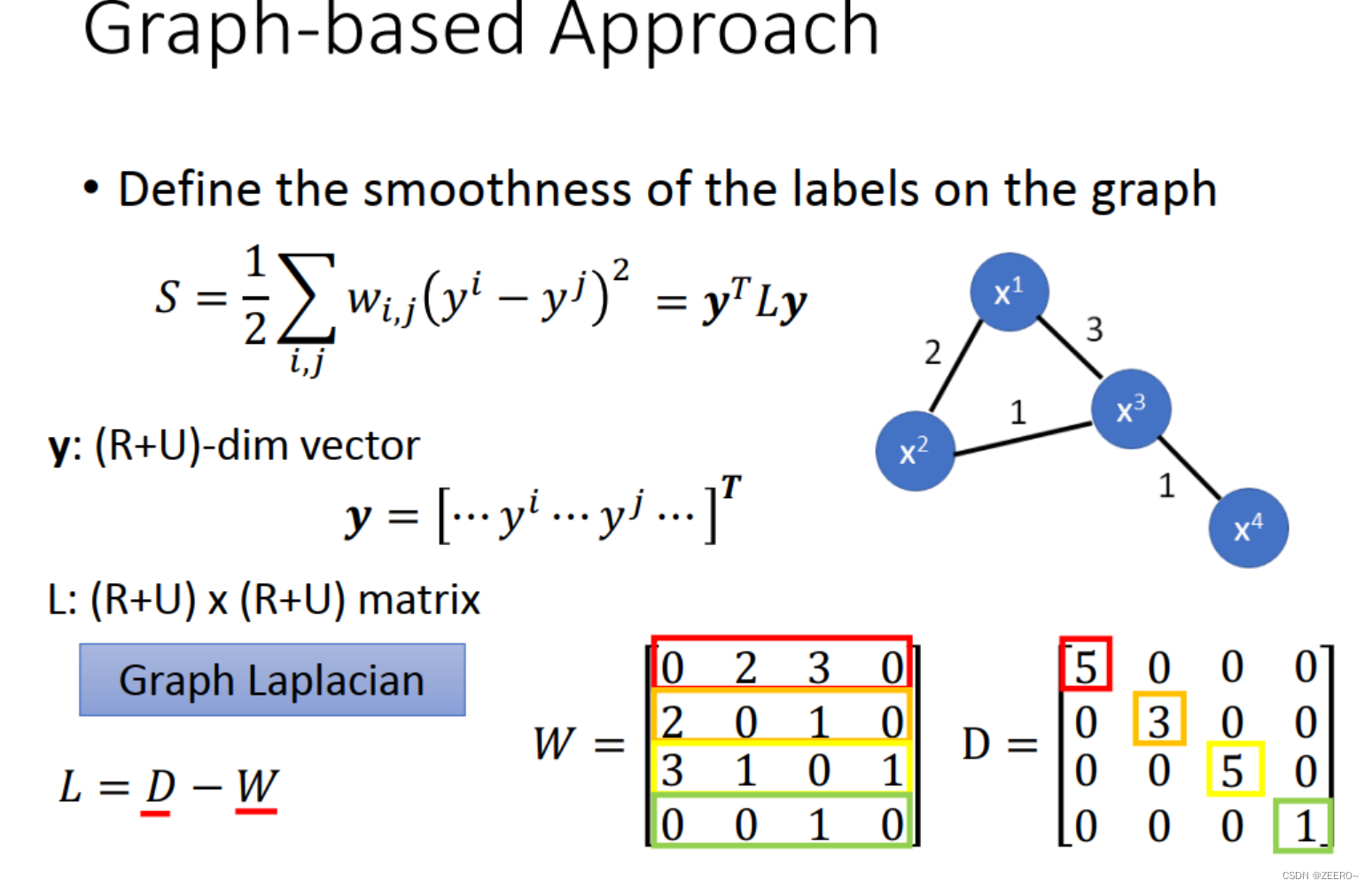
s的公式描述可以简化写成上图中的公式。其中W就是每个点之间的连接权重。例如说x1和x2之间的权重是2，因此w[1,2]和x[2,1]均为2.D则是一个对角矩阵，将w的每一行加起来刚好可以得到D上的对角元素。L也称为Graph Laplacian。

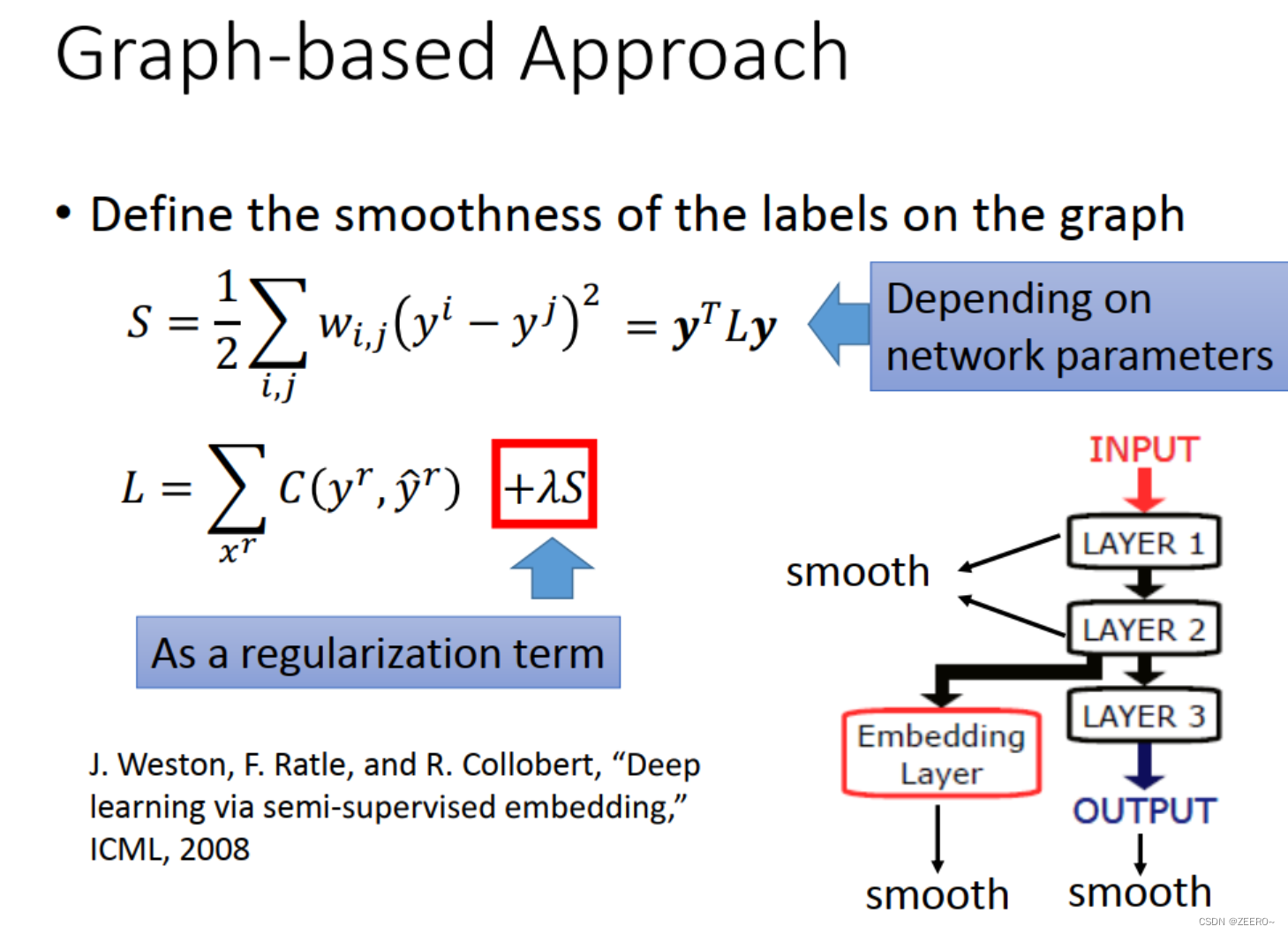
在训练ANN模型时，我们可以将smoothness作为损失项加入进去，类似于正则项一样。当然，这个smooth可以放在网络结构的任何地方，不一定要求输出要smooth，也可以要求其他地方要smooth。