《文献阅读》- 遗传算法作为量子近似优化算法的经典优化器（未完成）

文章目录

标题
摘要
关键词
结论
研究背景
- 1.介绍
研究内容、成果
- 3. 量子近似优化算法：基本概念及应用
常用基础理论知识
- 2.相关工作
- 酉矩阵
潜在研究点
文献链接

标题

Genetic algorithms as classical optimizer for the Quantum Approximate Optimization Algorithm

参考引用：
Acampora G, Chiatto A, Vitiello A. Genetic algorithms as classical optimizer for the Quantum Approximate Optimization Algorithm[J]. Applied Soft Computing, 2023, 142: 110296.

文献链接

摘要

优化是量子计算可以带来显着优势的研究领域之一。在这种情况下，混合量子经典变分算法，即量子近似优化算法（QAOA），因其有效解决组合优化问题的潜力而受到广泛关注。这种方法的工作原理是使用经典优化器来识别问题相关量子电路的适当参数，最终执行优化过程。不幸的是，学习最合适的 QAOA 电路参数是一项复杂的任务，受到多个问题的影响，例如以许多局部最优为特征的搜索环境。此外，在这种情况下开创的基于梯度的优化器往往会浪费量子计算资源。因此，无梯度方法正在成为解决此参数设置任务的有前途的方法。所提出的进化方法已在解决噪声量子设备上具有 5 至 9 个节点的图的 MaxCut 问题时进行了评估。结果表明，所提出的遗传算法通过实现具有更好近似率的解决方案，在统计上优于最先进的无梯度优化器。

关键词

遗传算法量子近似优化算法量子计算量子优化算法

结论

研究背景

1.介绍

1981 年，诺贝尔奖获得者理查德·费曼 (Richard Feynman) 假设基于量子原理的计算将在解决经典计算机难以解决的问题方面带来显着优势 [1]。 1985 年，当 David Deutsch 引入通用量子计算机的概念时，这一假设得到了完善，通用量子计算机是一种能够完美模拟每个有限的、可实现的物理系统的理论机器 [2]。从那时起，在量子器件的开发和量子算法的设计方面都取得了许多成就，与经典算法相比，性能得到了提高。特别是，从第一个角度来看，IBM、谷歌等大公司都在设计和开发真正的量子设备。具体来说，当前的量子计算机基于所谓的噪声中尺度量子（NISQ）技术[3]，其中设备配备了50-100个量子位（即量子信息的基本单位），这超出了我们的能力范围。由现有最强大的经典超级计算机通过强力模拟，尽管它们仍然具有对这些量子位的不完美控制的特征（因此术语“噪声”被解释）[4]。从算法的角度来看，非常著名的 Shor 算法和 Grover 算法已经成功地实现了相对于经典算法的量子优势：前者在多项式时间内找到整数的素因数；后者在多项式时间内找到整数的质因数。后者致力于在 O(√N) 时间内搜索非结构化数据，其中 N 是条目数，而执行相同操作的最佳经典算法的复杂度是 O(N) [5]。这些算法的成功来自于量子计算固有的大规模并行性，主要基于叠加和纠缠的概念。量子计算的并行性也可以为优化研究领域带来显着的好处。特别是在这种背景下，量子近似优化算法（QAOA）因其有效解决组合优化问题的潜力而受到广泛关注。事实上，自从引入以来，QAOA 已被应用于几个不同的问题，例如尾部分配问题 [6] 和最大 k 着色问题 [7]。具体来说，QAOA 属于变分量子算法的范畴，因为它遵循混合经典量子方案。准确地说，量子计算机用于运行以自由实数参数为特征的量子电路，计算优化问题的解，而经典计算机用于找到这些参数的最优值。通常，为了实现此目标，需要使用经典优化器。一般来说，这使用迭代方法，从猜测最佳参数开始。然后，在每次迭代中，量子电路使用参数的当前值运行以获得优化过程的结果，并通过成本函数评估该结果以相应地更新量子电路参数，直到达到终止标准，例如达到迭代次数。

不幸的是，由于几个问题，优化 QAOA 量子电路参数的任务可能很困难。特别是，最近的研究表明，QAOA 中的搜索景观是非凸的，并且包含许多局部极小值 [8]。此外，如上所述，QAOA量子电路的优化过程利用了量子计算机，这是一种不应该浪费的资源。因此，当经典优化器对量子设备执行少量调用时，它是好的。用于 QAOA 的第一个经典优化器是基于梯度的方法，因为它们在经典学习方法中取得了成功。然而，基于梯度的方法往往会陷入局部最小值，并多次调用量子设备来计算成本函数的导数。因此，应用无梯度方法的想法正在出现，该方法由不依赖成本函数导数的优化方法组成。正如 Fernández-Pendás 等人的工作中所报告的，应用无梯度优化器的首次尝试是有希望的。 [9]，但是找到一个好的经典优化器来保证 QAOA 的良好性能仍然是一个悬而未决的问题。

从这些考虑出发，本文首次提出将进化方法，特别是遗传算法应用于优化 QAOA 参数化量子电路的任务。所提出的遗传算法遵循配备精英主义的标准结构。所提出的遗传算法所解决的优化问题的解代表了 QAOA 电路的真实参数集。该方法的适用性在一次实验中得到了证明，该实验涉及应用所提出的进化方法来优化 QAOA 量子电路，该电路致力于通过考虑具有 5 至 9 个节点的图实例来解决 MaxCut 问题。这些实验是在有噪声的量子处理器上进行的，以展示所提出的方法在真实的不理想场景中的性能。结果表明，所提出的遗传算法在统计上优于最先进的无梯度方法，在优化领域的众所周知的度量（即近似比）方面获得了更好的解决方案。

论文的其余部分如下。第 2 节描述了用于学习 QAOA 参数的经典优化器的最新技术。第 3 节介绍了 QAOA 以及有助于理解量子计算的基本概念。该手稿的核心是对设计的遗传算法的描述，该算法用作 QAOA 的经典优化器，并在第 4 节中进行了报告。在第 6 节中得出结论之前，为显示所提出的方法的优点而进行的实验在第 5 节。

研究内容、成果

3. 量子近似优化算法：基本概念及应用

量子近似优化算法（QAOA）是一种混合经典量子算法，结合了量子电路和这些电路的经典优化[12]。QAOA的目标是解决组合优化问题，实际上，QAOA应用的典型问题就是所谓的MaxCut。本节致力于描述 QAOA 以及理解它所需的量子计算的基本概念。此外，本节还讨论了 MaxCut 问题，以了解 QAOA 如何应用于组合优化问题。

3.1.量子计算的基本概念
正如经典计算机使用电线和逻辑门来实现经典算法一样，基于电路的量子计算模型也使用电线和量子可逆门来模拟量子算法并操纵编码为量子位（qubit）的量子信息。

从数学上讲，量子位的一般状态用 Bra-ket 表示法或狄拉克表示法 [31] 表示，如下所示：
在这里插入图片描述
其中 α1 和 α2 是复数，称为振幅，逻辑状态 |0⟩ 和 |1⟩ 是构成计算基础的正交向量。这种逻辑状态的线性组合（称为叠加）在执行测量时会崩溃：
具体来说，当测量量子位时，幅度的平方模代表 |q0 ⟩ 在相应的经典逻辑状态下崩溃的概率。由于概率守恒，量子位状态 |q0 ⟩ 必须进行归一化，即 |α1|² + |α2 |² = 1。

类似地，n个量子位寄存器的一般量子态 |qn ⟩ 是 2ⁿ 个基态的线性叠加，如下：
在这里插入图片描述
其归一化条件为: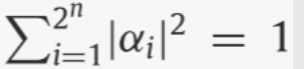

在这个多量子位系统中，|αi|²，其中 i = 1，… , 2ⁿ 是当寄存器的所有量子位都被测量时 |qn ⟩ 崩溃为第 i 个 n 位串的概率。

如上所述，量子门允许我们在 n 量子位寄存器上执行操作。具体来说，量子门是对量子位线性作用的酉算子 U，如下所示：
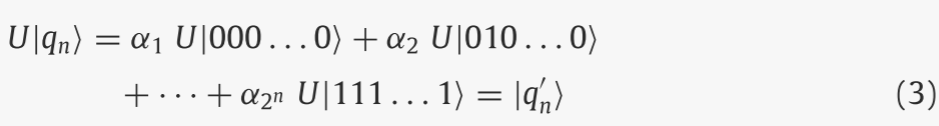
在这里插入图片描述

因此，表示量子门的一种便捷方法是使用酉矩阵，通过与量子态向量相乘来变换量子态。就像在经典情况下一样，量子逻辑运算可以在一个或多个量子位上执行，分别称为单量子位门和多量子位门。准确地说，作用于 n 个量子位的量子门由 2n × 2n 酉矩阵表示。在许多可用的量子门中，本节仅描述那些对 QAOA 设计有用的量子门。首先，Hadamard 门 H 是一个单量子位门，当它作用于每个单一计算基础时，它允许创建 |0⟩ 和 |1⟩ 的叠加。形式上，与 Hadamard 门相关的酉矩阵如下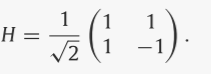：在这里插入图片描述

例如，通过考虑量子态 |0⟩，哈达玛门的应用会产生以下新的量子态 |q′⟩：
在这里插入图片描述

常用基础理论知识

2.相关工作

在文献中，用于训练 QAOA 的经典优化器属于两类：基于梯度的方法和无梯度方法。基于梯度的方法首先在文献[10-12]中进行了研究，因为它们成功应用于深度学习模型的训练，其训练方案类似于变分模型。具体来说，基于梯度的方法需要在优化过程中评估量子处理器上的成本函数梯度，因此为此目的设计了一些协议。除了朴素有限差分方案之外，参数移位规则还提供了通过在存在指定门的情况下执行两个不同电路来评估解析梯度的机会[13]。分析梯度也可以通过使用具有单个电路和附加辅助量子位 [15] 的 Hadamard 测试 [14] 来评估。因此，当使用基于梯度的技术时，需要在查询、量子位和操作的数量方面付出更多的努力和利用量子资源来实现这些协议，这些协议提取要在所有优化过程中使用的梯度信息。从这个考虑出发，这些方法不适合当前量子计算机，属于所谓的噪声中尺度量子（NISQ）时代，其中量子比特的数量是有限的。因此，第二类方法，即无梯度方法，正在出现，用于训练 QAOA [16] 和一般的量子变分电路 [17]。准确地说，在文献中，无梯度方法，例如线性逼近约束优化（COBYLA）[18]、Nelder–Mead [19]、修正鲍威尔方法[20]和同时扰动随机逼近（SPSA）[21]已经被采用应用于训练 QAOA [9]，因此，它们代表了 QAOA 无梯度优化器的最新技术。无梯度技术的好处是它需要使用更少的量子资源。事实上，它充当一个黑匣子，仅需要作为量子处理器的输出获得的成本函数的值作为输入。

此外，最近的研究表明，QAOA 中的成本函数景观是非凸的，具有许多局部极小值 [8]。这使得最优解的搜索变得复杂，特别是对于可能陷入局部最小值的基于梯度的方法。此外，在扩展这些近期架构时，成本函数景观中所谓的贫瘠高原可能会限制 QAOA 的可训练性 [22]。准确地说，随着涉及的量子位数量的增加，成本函数的梯度呈指数消失[23,24]：这意味着在大规模应用中成本函数景观变得更加平坦，使得寻找最优解决方案变得更加困难。由于这些原因，找到一个好的经典优化器来保证 QAOA 的良好性能仍然是一个悬而未决的问题。

在本文中，我们建议首次应用遗传算法作为无梯度方法来解决训练 QAOA 的这一艰巨任务。我们的建议得到了以下事实的支持：在机器学习和化学等变分量子算法的某些应用中，进化算法已被认为是替代的无梯度方法。特别是，在机器学习的背景下，遗传算法已应用于训练量子分类器[25]，并定义一组允许的门和量子自动编码器使用的最大数量[26,27]。在化学中，变分量子算法通常用于通过定义适当的参数化量子电路（所谓的 ansatz）来查找分子的基态能量 [28]，该电路能够近似相应分子的基态。在这种情况下，协方差矩阵适应进化策略已被用作[29,30]中的经典优化器。正如我们的实验结果所示，相对于已经应用于优化 QAOA 电路参数的最先进的无梯度方法，所提出的遗传算法本身是训练 QAOA 的良好解决方案。