目录
一.简介
二、2D变换
1. 等距变换(欧式变换)
2. 相似变换
3. 仿射变换
4. 射影变换(透视变换)
5. 结论
三、影消点与影消线
1. 平面上的线
2. 直线的交点
3. 2D无穷远点
4. 无穷远直线
5. 无穷远点的透视变换与仿射变换
6. 无穷远线的透视变换与仿射变换
7. 空间中的面和直线
8. 三维空间中的无穷远点(空间中平行线的交点)
9. 影消点
10. 影消线(视平线)
11. 无穷远平面
12. 两组平行线的夹角和影消点的关系
三、单视图重构
1. 单视图标定
2. 单视图重构
一.简介
双目视觉是利用两个摄像头或者图像传感器来模拟人类双眼之间的距离差异(即视差)而实现对物体深度信息的获取和三维立体重建。通过计算两个视角下的物体位置差异,可以得出物体相对于相机的距离,进而实现深度估计和三维重建。在机器视觉、机器人、虚拟现实、增强现实等领域有广泛应用。
单视图测量是指利用一张图像对其中物体的几何尺寸进行估计的方法。它常用于工程、制造、建筑等领域中对物体尺寸和形状进行快速测量和分析。
单视图测量通常涉及以下步骤:
-
选择测量对象和拍摄一张图像:从需要测量的物体中选择需要测量的特征,并拍摄一张包含这些特征的图像。
-
估计物体尺寸:使用现有的相机参数和基本几何知识(如三角测量、比例关系等)来推断图像中物体的几何尺寸。也可以使用相对高级的计算机视觉技术(如结构光、影像匹配等)来提高测量精度和效率。
-
验证测量结果:根据实际测量需求,对测量结果进行验证和校准,例如与现场实际测量值进行比较,或者使用多个视角的测量结果进行融合和校正。
单视图测量的优点在于其简单、直观,不需要额外的传感器和测量设备。但是,由于只利用一张图像进行估计,存在一定的误差和不确定性,尤其是物体形状和光照变化较大时。因此,在实际应用中,通常需要结合其他测量方法和技术来提高精度和可靠性。
二、2D变换
1. 等距变换(欧式变换)
等距变换(Isometric Transformation),也被称为刚体变换(Rigid Transformation),是指在二维或三维空间中保持物体的形状、大小和长度不变的变换。
等距变换包括平移(Translation)、旋转(Rotation)和镜像(Reflection)三种基本操作。平移是沿着某个方向将物体整体移动一定距离,旋转是围绕某个点进行旋转角度的变换,而镜像则是通过翻转物体使其对称。
在二维空间中,等距变换可以表示为:
平移变换:
[x'] [1 0 tx] [x]
[y'] = [0 1 ty] [y]
旋转变换:
[x'] [cosθ -sinθ] [x]
[y'] = [sinθ cosθ] [y]
镜像变换:
- 对x轴镜像:
[x'] [1 0] [x]
[y'] = [0 -1] [y]
- 对y轴镜像:
[x'] [-1 0] [x]
[y'] = [0 1] [y]
- 对原点镜像:
[x'] [-1 0] [x]
[y'] = [ 0 -1] [y]
在三维空间中,等距变换的表示方式类似,只是需要增加更多的维度和参数来描述物体的移动、旋转和镜像操作。
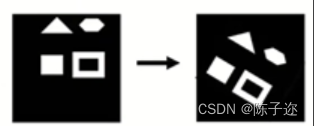
特点:
- 不变量:长度、面积
- 3个自由度
- 适合描述刚性物体的运动
2. 相似变换
相似变换(Similarity Transformation)是指保持物体形状和比例关系的变换,包括平移、旋转和缩放这三种基本操作。
在二维空间中,相似变换可以表示为:
平移变换:
[x'] [1 0 tx] [x]
[y'] = [0 1 ty] [y]
旋转变换:
[x'] [cosθ -sinθ] [x]
[y'] = [sinθ cosθ] [y]
缩放变换:
[x'] [s 0] [x]
[y'] = [0 s] [y]
其中,(x, y) 是原始点的坐标,(x', y') 是经过相似变换后得到的新点的坐标,(tx, ty) 是平移的向量,θ 是旋转角度,s 是缩放因子。
相似变换不改变物体的形状和比例关系,只是对物体进行位置的移动、旋转和缩放。它们都是线性变换,保持了直线的性质,但不一定保持角度、曲率等其他几何性质。
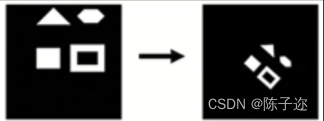
特点:
- 不变量:长度的比值、角度
- 4个自由度
3. 仿射变换
仿射变换(Affine Transformation)是指将一个点或物体通过线性变换和平移变换映射到另一个空间中的变换。它可以保持物体的平行性、直线性和比例关系,但不一定保持物体的角度和曲率。
仿射变换可以用线性代数的矩阵运算来表示,通常使用一个2x2矩阵表示旋转和缩放的部分,再加上一个2x1的平移向量。在二维平面上,仿射变换可以用如下矩阵形式表示:
[x'] [a b] [x] [tx]
[y'] = [c d] [y] + [ty]
其中 (x, y) 是原始点的坐标,(x', y') 是经过仿射变换后得到的新点的坐标,(a, b, c, d) 是旋转和缩放的参数,(tx, ty) 是平移的向量。
仿射变换在计算机视觉和图像处理中有广泛的应用,例如图像的旋转、放缩、平移、翻转等操作都可以通过仿射变换实现。此外,仿射变换还可以用于图像配准、图像校正、特征对齐、人脸识别等任务中。
值得注意的是,仿射变换是一种线性变换,它保持直线的性质,但不能保持曲线。如果需要处理非线性变换,例如透视投影,就需要使用更为复杂的射影变换(Projective Transformation)了。
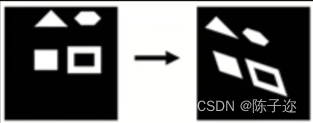
特点:
- 不变量:平行线、面积的比值
- 不能保持原有线之间的夹角关系
- 6个自由度
4. 射影变换(透视变换)
射影变换(Projective Transformation)是指将一个空间中的点或物体经过投影摄像机(perspective camera)或透视图(perspective view)的映射投影到另一个平面或空间中的变换。它通常可以用矩阵来表示,因此也被称为齐次坐标变换(Homogeneous Coordinates Transformation)。
射影变换是一种非线性变换,它可以用一个3x3的矩阵表示,并且由于其具有旋转、平移、缩放和投影等变换效果,因此它可以完成更为复杂的几何变换任务。在计算机视觉中,最常用的射影变换是针孔相机模型(Pinhole Camera Model)下的投影变换,该模型假设相机与场景之间的关系是透视投影。而在图像处理中,射影变换可以被用来实现各种图像的校正和纠偏,例如透视失真纠正、倾斜校正等。
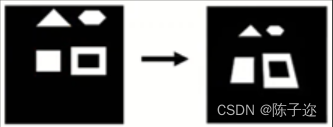
特点:
- 不变量:共线性、四共线点的交比
- 不能保持原有平行关系
- 8个自由度
5. 结论
- 欧式变换是相似变换的特例
- 相似变换是仿射变换的特例
- 仿射变换是透视变换的特例
三、影消点与影消线
1. 平面上的线
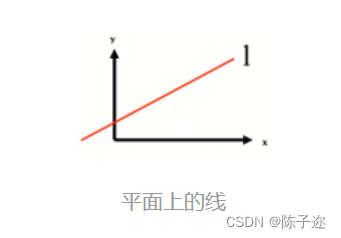
2. 直线的交点

3. 2D无穷远点
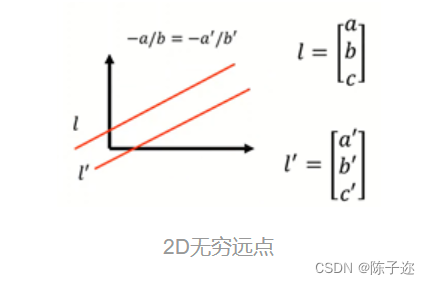
4. 无穷远直线
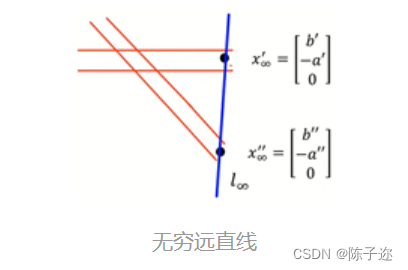
无穷远线是无穷远点的几何,也是平面上线的“方向”的集合。
5. 无穷远点的透视变换与仿射变换
无穷远点经透视变换不是无穷远点
无穷远点经仿射变换仍是无穷远点
6. 无穷远线的透视变换与仿射变换
无穷远线经透视变换不是无穷远线
无穷远线经仿射变换仍是无穷远线
7. 空间中的面和直线

空间中的直线定义为两平面的交线。一般用来描述直线的方向。
8. 三维空间中的无穷远点(空间中平行线的交点)
空间中平行线的交点
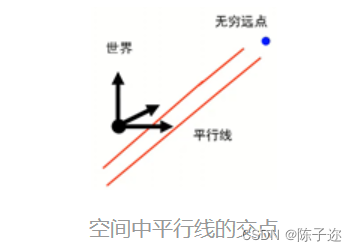
9. 影消点
定义:无穷远点在图像平面上的投影点
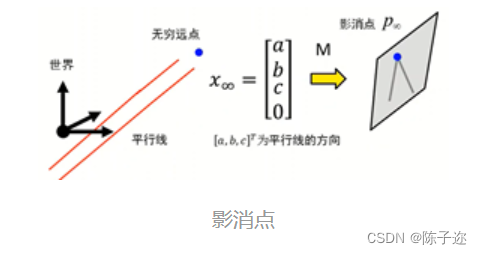
设空间中直线方向为
则影消点和直线方向满足以下关系:
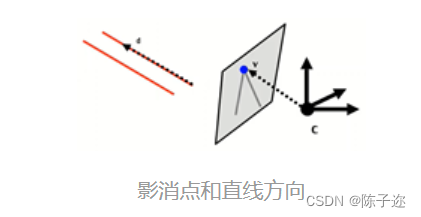
10. 影消线(视平线)
影消线是空间上同一平面的多个无穷远点经透视变换得到的影消点的集合,也是空间上无穷远线经透视变换得到的平面直线。
影消线和无穷远直线的关系:
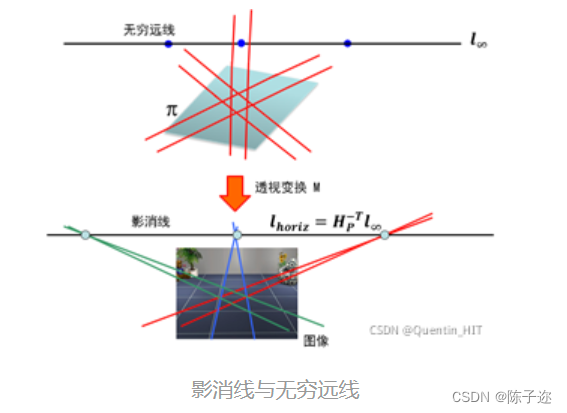
影消线和平面法向量之间的关系:

11. 无穷远平面
平行平面在无穷远处相交于一条公共线,称为无穷远直线。
两条或多条无穷远直线的集合定义为无穷远平面
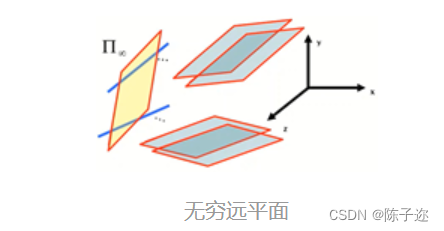
12. 两组平行线的夹角和影消点的关系
由影消点和直线方向的关系,
可以得到空间中两组平行线的夹角和影消点, 的关系:
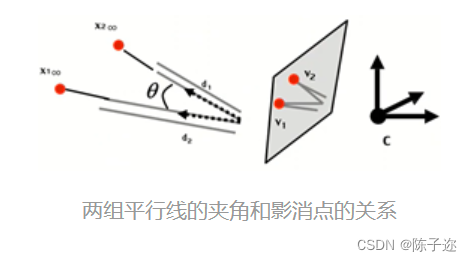
此外,有以下性质:

应用:
- 估计相机参数(单视图标定)
- 恢复三维场景结构
三、单视图重构
1. 单视图标定
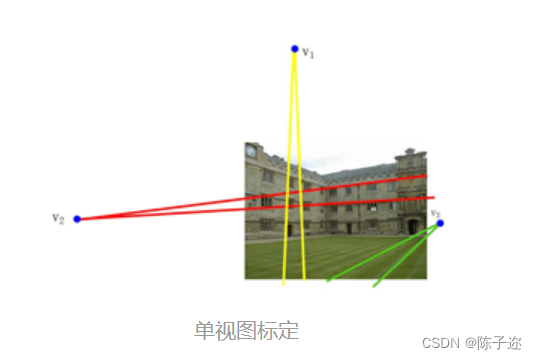
选取三个互相垂直的平面,分别找出三个平面上的影消点。可以列出下面三个方程:
有5个自由度,但只能列出三个方程。若假定零倾斜、正方形像素,则,即只剩下三个自由度。这样就可以根据三个影消点求解出相机内参数矩阵。
2. 单视图重构
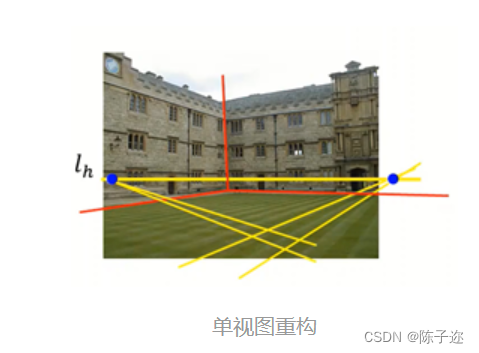
可以由两个影消点画出这一平面的影消线,根据之前求出的内参数矩阵/(K/),即可得到这一平面的法向量:
同理可以求出另外两个平面的法向量。根据三个平面的方程,即可重构出画面。
注意:
场景的实际比例无法恢复;
需要手动选择影消点和影消线;
需要场景的先验信息,如点对应的关系,线、面几何信息等等。
单幅视图2D到3D的映射具有多义性