【算法练习Day24】递增子序列全排列全排列 II

在这里插入图片描述

📝个人主页：@Sherry的成长之路
🏠学习社区：Sherry的成长之路（个人社区）
📖专栏链接：练题
🎯长路漫漫浩浩，万事皆有期待

文章目录

递增子序列
- 容易出错的地方
全排列
全排列 II
总结：

递增子序列

491. 递增子序列 - 力扣（LeetCode）
在这里插入图片描述

递增子序列也是一道求子集的问题，但是这道题与子集II的不同之处是，这道题不能够对数组排序，而且要求求出答案序列为2以上的递增子序列。

不能排序求递增子序列是有点难度的，需要一些技巧，首先给定数组nums可能含有重复数据，而做过往期的朋友都知道，去重是一定要排序的，那么不排序我们怎么做呢？

思路是这样的，在函数实现的内部，我们定义一个哈希表，该哈希表存储的是当前数层中我们取过那些数据，取过的我们标记一下，这里用数组还是其他什么做哈希都可以，但是数组更高效。

代码如下：

class Solution {
public:vector<vector<int>> result;vector<int> path;void backtracking(vector<int>&nums,int startIndex){if(path.size()>1){result.push_back(path);}unordered_set<int> uset;for(int i=startIndex;i<nums.size();i++){if((!path.empty()&&nums[i]<path.back())||uset.find(nums[i])!=uset.end()){continue;}uset.insert(nums[i]);path.push_back(nums[i]);backtracking(nums,i+1);path.pop_back();}}vector<vector<int>> findSubsequences(vector<int>& nums) {result.clear();path.clear();backtracking(nums,0);return result;}
};

没有接触过不能排序而去重的逻辑，有时候还真的想不出来这种解法，因为它是在递归函数内部中间创建的哈希表，我们并不需要对它进行回溯，原因是每进入下一层递归，也就是增加了递归深度它会新建一个哈希，来保存当前树层所插入过的节点，换句话说它保存的是树的横向结构。我们在for循环中，通过判断该层的哈希里要插入的数据有没有插进去过，即可完成数层去重。而控制递增子序列就显得格外简单了，我们仅仅是比较一下当前我们要插入的合法数据和要插入的数组的最后一个数据谁大就可以了，如果要插入的大直接插入，不行的话还是continue，理由还是相同的，continue是为了能让i往后走，找之后的数据看看能不能接着插入进数组。

容易出错的地方

由于我们是根据题目给定数组nums对应的个数据做的哈希，为了判断这个数是否在该树层用过。当我们用数组做哈希结构，要注意测试用例的数据范围，数据包含负数，且是-100-100的数据，所以我们用201个空间并且使数据主动加上100，来避免对负数下标的访问，这是有讲究的定义数组，而非随便取数组大小。当然选用set或者map可以避免这方面的判断，但是当数据范围不大时候，选用数组做哈希可以提高运行效率。

全排列

46. 全排列 - 力扣（LeetCode）
在这里插入图片描述

终于进到了回溯算法的下一个主题，全排列，到了排列部分也就意味着我们的回溯算法例题，快要进入尾声了。排列和组合的模板不同。换句话说，组合问题，子集问题，切割问题三种问题实际上都可以类比为组合问题的大类里面，因为无论是子集问题还是切割问题，都是不能向前去取数

但是排列可以，{1，2}和{2，1}是完全不同的排列，这就意味着我们在写递归时要考虑到这一点，如何即清楚我们下一层从哪里开始，又要可以遍历到这个数之前的数据呢？答案是用到一个数组来保存，这个数组标识着我们哪些数已经取过了，哪些数没有取，也就是说排列问题（往回取数的问题）无论是否涉及到去重都要加入一个标记数组。

先看代码分析

class Solution {
public:vector<vector<int>> result;vector<int> path;void backtracking(vector<int>& nums,vector<bool>&used){if(path.size()==nums.size()){result.push_back(path);return;}for(int i=0;i<nums.size();i++){if(used[i]==true){continue;}used[i]=true;path.push_back(nums[i]);backtracking(nums,used);path.pop_back();used[i]=false;}}vector<vector<int>> permute(vector<int>& nums) {result.clear();path.clear();vector<bool> used(nums.size(),false);backtracking(nums,used);return result;}
};

用标记数组是如何实现的呢？在取数之后做标记，往深层递归时，由于被取过的数仍然被标记着，我们可以让i=0每次让它从第一个数开始找，碰到没有被标记的我们直接加入path中，那么是如何像示例中一样，由{1，2，3}逐渐转变为{2，1，3}的呢？实际上也是由于回溯，回溯删除1之后，此时i=0上去i++变为1，这个时候取到的是nums[1]也就是2了，递归问题的取数有时候会突然想不明白，可以自己用编译器调试一下看看，递归是如何进行的，回溯又是如何回溯的，多调试才有利于对递归更深的了解。

全排列 II

47. 全排列 II - 力扣（LeetCode）
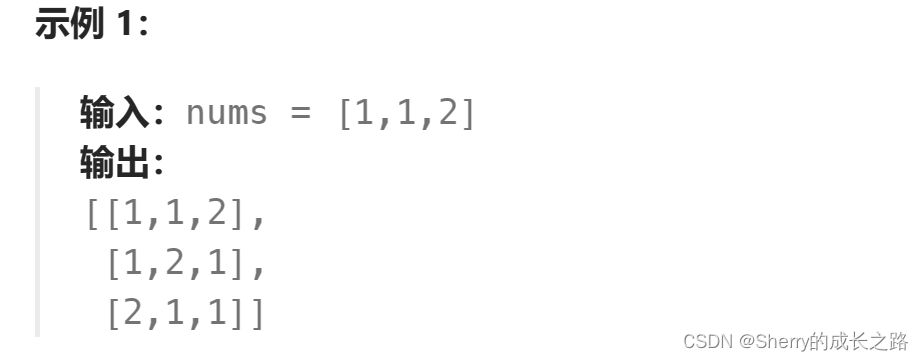
在这里插入图片描述

知道了全排列的做法，那么全排列II也就变得简单一些了，一样的套路加上对数据的树层（横向上）去重就可以达到题目要求的效果了。这里可能会想，我们这道题的去重也要重新定义一个新的数组来保存吗？

肯定是不需要的，我们的标记数组也就是去重数组，因为它们都是起到标记一个数是否被取到，所以两个思路用一个数组是完全可以的。依旧是将给定数组先进行排序，使相同的数据挨在一起，这样才有利于排序，去重时完全按照以往去重的规则。

class Solution {
private:vector<vector<int>> result;vector<int> path;void backtracking (vector<int>& nums, vector<bool>& used){// 此时说明找到了一组if (path.size() == nums.size()) {result.push_back(path);return;}for (int i = 0; i < nums.size(); i++) {// used[i - 1] == true，说明同一树枝nums[i - 1]使用过// used[i - 1] == false，说明同一树层nums[i - 1]使用过// 如果同一树层nums[i - 1]使用过则直接跳过if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) {continue;}if (used[i] == false) {used[i] = true;path.push_back(nums[i]);backtracking(nums, used);path.pop_back();used[i] = false;}}}
public:vector<vector<int>> permuteUnique(vector<int>& nums) {result.clear();path.clear();sort(nums.begin(), nums.end()); // 排序vector<bool> used(nums.size(), false);backtracking(nums, used);return result;}
};