Hi,你好。我是茶桁。

之前的课程中，我们学习了两个最重要的回归方法，一个线性回归，一个逻辑回归。也讲解了为什么学习机器学习要从逻辑回归和线性回归讲起。因为我们在解决问题的时候，有限选择简单的假设，越复杂的模型出错的概率也就越高。

本节课中，我们要继续我们未完成的内容。

还记得，咱们上一节课中最后所说的吗？在完成了基本回归之后，该如何去判断一个模型的好坏，以及如何调整和优化。

好，我们开始本节课程。

PICKLE

本节课中，会重点的给大家做一件事，叫「评测指标」。

在这之前，我们发现了一个麻烦事。就是我们现在需要去观测我们的分类结果，我们不得不再去执行一遍我们之前的训练程序，拿到最后的分类结果：

RM:6.38, LSTAT:24.08, EXPENSIVE:0, Predicated:0
...
RM:6.319, LSTAT:11.1, EXPENSIVE:1, Predicated:0

这很麻烦，训练结果每次要使用的时候都需要运行一次，这样非常的麻烦。现在我想要把这个model不要每一次都训练一下,而是要把它做一个保存，下次用的时候不需要从头到尾再训练一次。

现在现在，可以给他做一个persistence，做一个留存。现在就是要做这么一件事情。

import picklewith open('logistic_regression.model', 'wb') as f:pickle.dump(model, f)with open('w.model', 'wb') as f:pickle.dump(w, f)with open('b.model', 'wb') as f:pickle.dump(b, f)print('pickle finished')---
pickle finished

并且最后我得到了三个文件，分别是logistic_regression.model, w.model以及b.model。

现在就可以把训练完成的model做保存了。之后我们用Pytorch, tenserflow之类的做，它都有这样的功能。

到这一步之后，我们上一节上所写的代码就可以暂时不用了。不过为了整个代码的完整性，我仍然将其又在本节课的10.ipynb内些了一遍。

那么，我们要用的时候怎么办呢？如果要用这个对象的时候，将我们之前对文件操作的代码拿过来，然后将其中的wb参数改成rb，然后再将二进制文件读取一遍：

with open('logistic_regression.model', 'rb') as f:model_r = pickle.load(f)with open('w.model', 'rb') as f:w_r = pickle.load(f)with open('b.model', 'rb') as f:b_r = pickle.load(f)print('pickle read finished')

rb的意思是read binary，也就是读取二进制文件。然后，为了在测试的时候避免混乱，让我接下来所使用的文件使用的是我重新读取的模型而不是之前训练时生成的的，我将重新读取的这几个文件命名为model_r，w_r,b_r。

那再之后，虽然不用重新训练了，但是数据还是要读取一遍的，并且，按照训练数据的规则重新整理好, 都完善了之后，就可以开搞进行分类了。

import pandas as pd
from sklearn.datasets import fetch_openmldataset = fetch_openml(name='boston', version=1, as_frame=True, return_X_y=False, parser='pandas')data = dataset['data']
target = dataset['target']dataframe = pd.DataFrame(data)rm = dataframe['RM']
lstat = dataframe['LSTAT']
dataframe['price'] = dataset['target']greater_then_most = np.percentile(dataframe['price'], 66)
dataframe['expensive'] = dataframe['price'].apply(lambda p: int(p > greater_then_most))expensive = dataframe['expensive']
random_test_indices = np.random.choice(range(len(rm)), size=100)
decision_boundary = 0.5for i in random_test_indices:x1, x2, y = rm[i], lstat[i], expensive[i]predicate = model_r(np.array([x1, x2]), w_r, b_r)predicate_label = int(predicate > decision_boundary)print('RM:{}, LSTAT:{}, EXPENSIVE:{}, Predicated:{}'.format(x1, x2, y, predicate_label))

评测指标

好，解决了模型的重复使用之后，我们再回到课程中继续。

很多人在学习过程中，会觉得「评测指标」是一个没有那么有趣的事情。比方说，咱们学模型，学算法，就可以去写程序，可以运行，写出来的时候会感觉还蛮酷的。但是评测指标呢，很多同学就觉得不是那么有趣。

其实，我想告诉大家，评测指标是一个非常重要的东西。好比完成任何一个任务，不管你现在是完成普通的编程任务，还是要完成一个公司的市场行为、运营行为。一般来说，越复杂的任务，只要把评价指标，评价方式做对，这个任务基本上就已经完成了一半了。

对于我们来说，工作的时候要知道，对于一个机器学习任务，能找到正确的评测指标，这个机器学习任务就已经成功一半了。

首先，来看一个问题：Losses持续下降，到底是意味着什么呢？

import matplotlib.pyplot as plt
%matplotlib inline
plt.plot(losses)

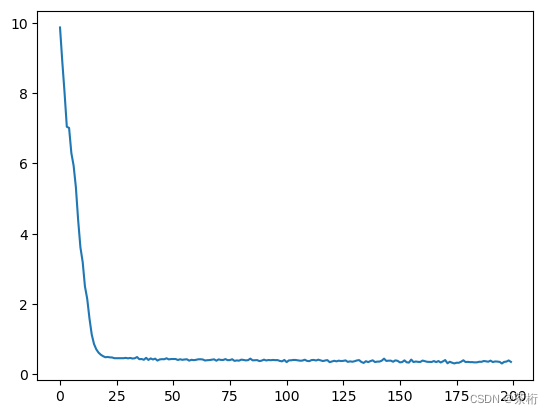
loss持续下降意味着误差越来越小?方向是对的?测试值更加接近真实值?更精确的说法是，它在逼近最优解，但是效果是不是特别好，还不知道。

接下来这个问题是一个比较复杂的问题，是一个难点：

-np.sum(y * np.log(yhat) + (1 - y) * np.log(1 - yhat))

这段代码是我们写的loss函数， 我们现在来假设有一组数据:

true_label = np.array([1, 0, 1, 0, 1]) # 二分类

再假设有一个模型，在执行的时候，它会知道咱们做的是一个二分类问题，那么结果就是不是1，就是0。这个时候模型有可能偷懒，那给到的数据就会是随机的，好吧，开个玩笑，其实就只是因为数据不足造成给到的数据过于随机：

predicate_1 = np.array([0.8, 0.7, 0.8, 0.3, 0.8])

然后我们执行算法来拿到结果：

def test_lose(y, yhat):return -np.sum(y * np.log(yhat) + (1 - y) * np.log(1 - yhat))
test_lose(true_label, predicate_1)---
2.2300784022072975

现在我们拿到的值为2.23，不过要记得，咱们这只是一个假设值。那这个时候引入我们刚才谈到的loss的曲线，loss是持续下降的，当它下降到最低的值的时候依然比这个2.23还要高，那就说明这个模型都还没有随机猜测的准确度高。

这个情况其实是经常会遇到的一个问题，你会看到你的的模型一直在下降，下降的非常好，但是一做实际测试的时候效果就特别差。

再换个说法就是，这个模型跑的时候，瞎猜的值都有2.23的准确，但是loss虽然一只在下降，一只下降到了3。虽然loss看起来在下降，但是这整个结果都不是太好。

瞎猜的时候的准确度，loss值，我们称为这个模型的Baseline。你的值最起码要比这个好。

所以就如之前所的，loss持续下降意味着模型在向着最优的方向在寻找，但并不意味着结果就会很好，因为有可能连瞎猜都不如。

好，以上是第一点，我们接着来看第二点。

loss一直在下降,但是我们现在想知道的是有多少个label预测对了。先建立两个变量来分别存储数据：

true_labels, predicated_labels = [], []...
for i in random_test_indices:...true_labels.append(y)predicated_labels.append(predicate_label)

然后分别获得了两组数据，一个是true_labels，一个是predicated_labels。有了这两组数据之后，我们来定义一个accuracy， 这个是预测的值和相似的值一共有多少个是一样的。

def accuracy(ytrues, ylabels):return sum(1 for yt, y1 in zip(ytrues, ylabels) if yt == y1) / len(ytrues)accuracy(true_labels, precicated_labels)---
0.89

0.89, 就是说有89%的label都是猜对了。

最早的时候其实只有这一个标记，但这个标记很容易出错。

假设有一个警察局，要在100个人里边判断谁是犯罪分子。现在我们知道有3个是犯罪分子，然后警察说这100个人全部都是犯罪分子。那么现在准确度有多少？

然后又有一个警察站出来说，这100个人都不是犯罪分子，那他的准确度又是多少？

我们现在让第一个警察是a，第二个警察是b。

警察b有97个标签都说对了，这会给人一种错觉，好像他预测的很准确的。但是其实，a和b两个人都判断的不准确。那我们这个时候就需要引出一个定义：Precision。

precision也是准确度的意思，和accuracy不同点是，accuracy的对比是对比目标和现有值是否匹配，匹配的就算正确。而precision除了看是否匹配之外，还要目标值，也就是positive。

这里举个例子说明一下，比如我们去检测是否有新冠病毒，那么目标是为了检测出有新馆病毒的人，那么呈阳性的人就是我们的positive， 那么我们precision除了预测出有新冠和没有新冠的人之外，有新冠的人也需要一一对应上，也就是positive要正确。

如果是写代码的话，也就是将之前的accuracy拿过来改改就可以直接用了：

def precision(ytrues, yhats):# 预测标签是1的里面，正确的比例是多少positives_pred = [y for y in yhats if y == 1]return sum(1 for yt, y in zip(ytrues, yhats) if yt == y and y == 1) / len(positives_pred)precision(true_labels, predicated_labels)---
0.8333333333333334

先将预测为1，也就是预测呈阳性的目标放到positives_pred中，再来检测一下在这些预测出来的目标中，预测对的有多少。

除此之外之外，还有一个值叫做recall，它的意思是在实际的positive里，有多少比例被找到了。

def recall(ytrues, yhats):true_positive = [y for y in ytrues if y == 1]     return sum(1 for yt, y in zip(ytrues, yhats) if yt == y and yt == 1) / len(true_positive)recall(true_labels, predicated_labels)---
0.8064516129032258

好，我们再来复盘一下这三个值，一个是accuracy, 一个是precision，一个是recall。

accuracy就是预测值和实际值有多少是一样的。但是有可能会在实际场景都不是很均衡。

precision是拿到预测后的目标值，然后拿这些目标的实际值去比较看有多大比例是一样的。

recall是先拿到实际的目标值，然后拿目标预测值比较看有多大比例是一样的。

根据我们之前说的警察抓坏人的那个假设，我们现在来做一个测试，假设我们现在好人有90个，坏人有10个。

people = [0] * 90 + [1] * 10
import random
random.shuffle(people)

现在警察a来了，就判断说：全部都是好人，把他们全部都放了吧。这样的话，它的accuracy是多少呢？accuracy就是预测的，只要是实际值的那个label就行。我们来看看：

a = [0] * 100
accuracy(people, a)---
0.9

我们看这个准确度就会很高，这个也能理解，因为警察a将这100个人中的90个好人全部判断准确了对吧？

让我们来看看其他两个：

precision(people, a)---
ZeroDivisionError: division by zero======
recall(people, a)---
0

precision警告我们分母为0，报错了。那分母为什么为0呢？因为a说了，所有都是好人，那么预测的目标值，也就是分母上的坏人就为0。

而recall呢，结果为0。这是因为分母上的坏人实际值虽然为10，但是预测的目标值，也就是分子上为0。那结果肯定是为0。

本来a的accuracy是0.9，别人还以为准确度很高，结果一个坏人都没抓住。这肯定不行。

那b的情况又如何呢？之前说过，b说所有的都是坏人，统统抓起来。

b = [1] * 100
accuracy(people, b)---
0.1========
precision(people, b)---
0.1=========
recall(people, b)---
1.0

虽然accuracy和precision都不高，但是似乎目标都被找出来了。颇有一种「宁可错杀1000，不可放过一个」的感觉。

那以上这些，就是为什么要有这3个非常重要的指标的原因。

好，那下一节课中，我们要来看看关于precition和recall的一个矩阵，这个矩阵呢，将会是我们工作中分析结果常用的。

$$\begin{array}{rl}Precision& =\frac{tp}{tp+fp}\\ Recall& =\frac{tp}{tp+fn}\end{array}$$