目录
1.红黑树概念
2.红黑树性质
3.调整
1.如果p和u都是红色,将其都改为黑色即可,然后向上调整
2.如果p红(u黑/u不在),这时候左子树两红,于是给右子树一个红(旋转+变色)
2.1右单旋 + 变色- p变黑, g变红, 达到给右子树一个红节点的效果, 并保持每条路径上黑色节点的个数相同
2.2左右双旋转 + 变色
2.3左单旋 + 变色
2.4右左双选 + 变色
4.红黑树的简单实现
4.1红黑树的定义
4.2相关功能
插入
检查
获取最左/右侧的节点
检查树种是否存在data节点
4.3默认成员函数
测试用例:
1.插入
2.检查
3.获取最左/右侧节点
4.在树种查找节点
1.红黑树概念
红黑树,是一种二叉搜索树,但在每个结点上增加一个存储位表示结点的颜色,可以是Red或Black。 通过对任何一条从根到叶子的路径上各个结点着色方式的限制,红黑树确保没有一条路径会比其他路径长出俩倍,因而是接近平衡的
2.红黑树性质
- 每个结点不是红色就是黑色
- 根节点是黑色的
- 如果一个节点是红色的,则它的两个孩子结点是黑色的
- 对于每个结点,从该结点到其所有后代叶结点的简单路径上,均包含相同数目的黑色结点
- 每个叶子结点都是黑色的(此处的叶子结点指的是空结点)
最短路径: 全黑
最长路径: 一黑一红交替
红黑树就能保证:其最长路径中节点个数不会超过最短路径节点个数的两倍
红黑树优势: 旋转次数更少
新插入的节点默认是红色
--1.如果是黑色, 一定违反了规则4 会影响所有路径
--2.如果是红色, 当插入到红色节点后面,违反规则3 , 当插入到黑色节点的后面,不违反规则
3.调整
什么时候需要修改红黑树?--当插入到红色节点后面的时候
1.如果p和u都是红色,将其都改为黑色即可,然后向上调整
- -然后将g改为红(g原来为黑,我们已经把p,u改为黑了,会多一个黑节点,违反规则4,需要把g改为红)
- -当然改为红后,g的p可能也是红,继续往上调整即可(把cur = g),如果最后调到根,要将根变黑
2.如果p红(u黑/u不在),这时候左子树两红,于是给右子树一个红(旋转+变色)
-这种情况讨论cur的插入位置 ,来决定其需要怎么旋转(单旋,双旋)
--p是g的左 ,且插入的节点在左子树
2.1右单旋 + 变色
- p变黑, g变红, 达到给右子树一个红节点的效果, 并保持每条路径上黑色节点的个数相同
2.2左右双旋转 + 变色
--p是g的右, 且插入的节点在右子树
2.3左单旋 + 变色
2.4右左双选 + 变色
4.红黑树的简单实现
4.1红黑树的定义
节点

RBTree

4.2相关功能
插入
1.找到节点的位置
2.链接节点
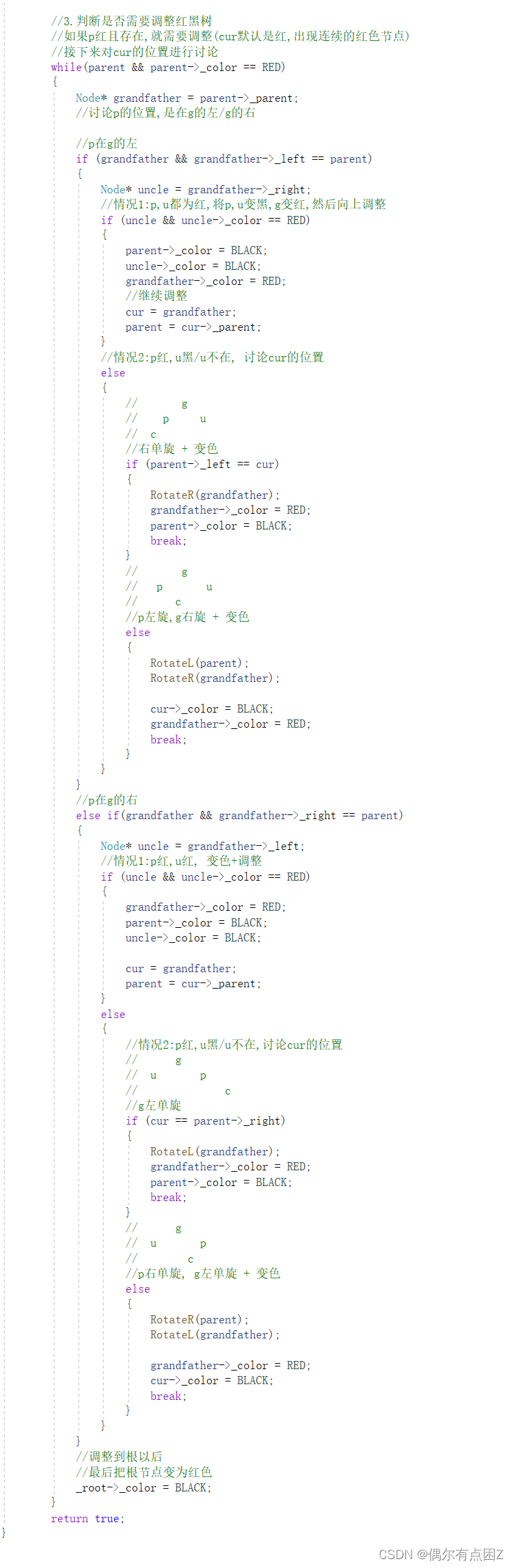
3.判断此时p是不是红色, 且存在 (默认插入的节点是红色), 是的话就需要调整
--p,u存在且都为红 ===> 直接将p,u变为黑色,g变红色, 然后向上调整,
如果调到根(要将其变黑)
--p红, u红/u不在 ===> 对插入节点位置进行讨论
1.p是g的左, cur是 p的左 ===> g右单旋
2.p是g的左, cur是p的右 ===> p左旋, g右旋
3.p是g的右, cur是p的右 ===> g左单旋
4.p是g的右, cur是p的左 ===> p右旋,g左旋
代码:
1.找到节点的位置 2.链接节点
3.判断此时p是不是红色, 且存在 (默认插入的节点是红色), 是的话就需要调整
效果:
检查
- 判断根节点是黑色的(规则2)
- 判断有无连续的红色节点(规则3)
- 判断每条路径上的黑色节点个数是否相等(规则4) --这里随便选取一条路径的黑色节点数作为基准值, 用来和对比其它路径黑节点的个数
代码:
//红黑树的检查bool Is_RBTree() {return _Is_RBTree(_root);}//红黑树的检查bool _Is_RBTree(Node* root){//规则2:根节点是黑色的if (root == nullptr) return true; if (root->_color != BLACK) return false;//规则3:不能有连续的红色节点//规则4:每条路径上的黑色节点个数相等Node* cur = root; int base_nums = 0;while (cur) {if (cur->_color == BLACK) base_nums++;cur = cur->_left;}Check(root,base_nums,0);}bool Check(Node* root,int base_nums,int block_nums) {if (root == nullptr) {if (base_nums != block_nums) return false;return true;}//检查有没有连续的红色节点if (root->_parent && root->_color == RED && root->_parent->_color == RED)return false;//遇到一个黑色节点就++if (root->_color == BLACK) block_nums++;return Check(root->_left,base_nums,block_nums) && Check(root->_right,base_nums,block_nums);}
获取最左/右侧的节点
//获取红黑树最左侧节点Node* LeftMost(){Node* cur = _root;//空树if (cur == nullptr) return nullptr;while (cur->_left){cur = cur->_left;}return cur;}//获取红黑树最右侧节点Node* RightMost(){Node* cur = _root;//空树if (cur == nullptr) return nullptr;while (cur->_right){cur = cur->_right;}return cur;}
检查树种是否存在data节点
//检测红黑树中是否存在值为data的节点Node* Find(const T& data){Node* cur = _root;while (cur){if (cur->_data > data)cur = cur->_left;else if (cur->_data < data)cur = cur->_right;else return cur;}return nullptr;}
4.3默认成员函数
--构造函数
这里传了缺省值(可不写)
--拷贝构造
思路:使用前序遍历, 构造红黑树
--赋值运算符
思路: 交换_root
--析构函数
后序遍历,删除节点
测试用例:
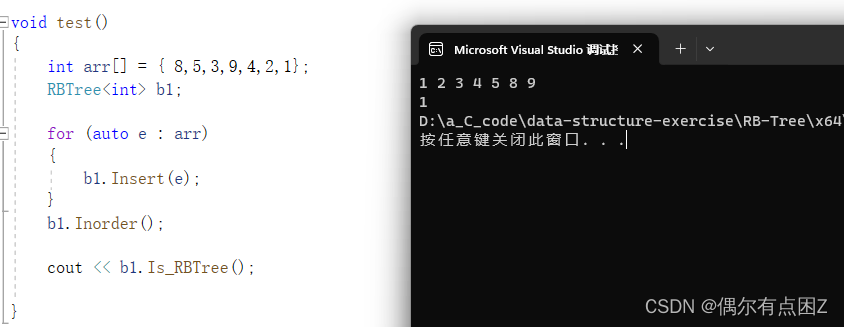
1.插入

2.检查
正常情况:
异常:
屏蔽掉颜色的调整

修改默认生成黑色节点

3.获取最左/右侧节点

4.在树种查找节点
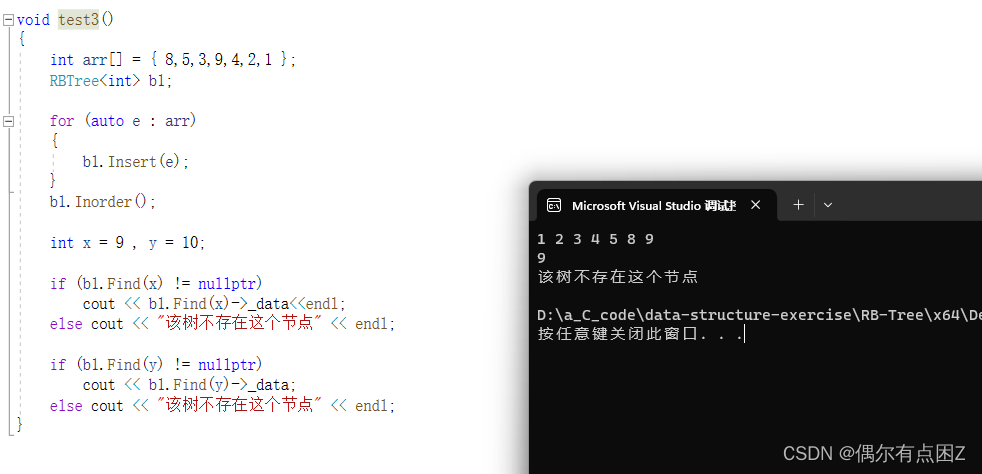
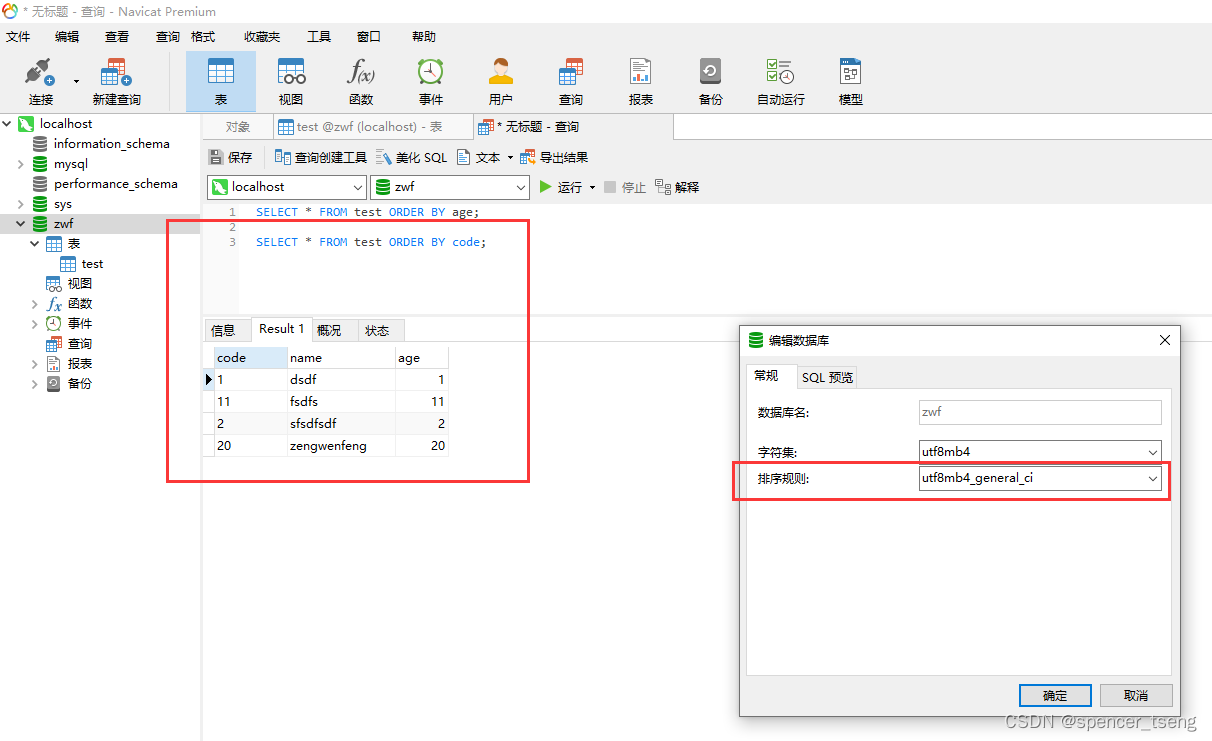
代码:RB-Tree/RB-Tree · 朱垚/数据结构练习 - 码云 - 开源中国 (gitee.com)











![类加载的过程总结以及双亲委派模型[JVM]](https://img-blog.csdnimg.cn/4038c3472ac3420faa056a595ebd10a5.png)