图片来自施泰德博物馆

一、前言
通过这些文章,我希望巩固我对这些基本概念的理解,同时如果可能的话,通过我希望成为一种基于直觉的数学学习方法为其他人提供额外的清晰度。如果有任何错误或机会需要我进一步阐述,请分享,我可以进行必要的修改。
这是关于线性代数基础知识的持续系列文章的第一个补充,线性代数是机器学习背后的基础数学。本文最好与David C. Lay,Steven R. Lay和Judi J. McDonald的线性代数及其应用一起阅读。将此系列视为外部配套资源。
二、背景
线性方程组和线性方程组在金融、工程、化学、计算机科学、统计学和物理学等领域具有各种实际应用。在化学中,线性方程用于平衡化学反应并计算反应物和产物的数量。线性代数的这一基石也出现在物理学中,其中线性方程在运动学和热力学中使用来描述物体的运动,帮助计算距离、速度和加速度,并分别模拟物理系统中的传热和能量流。金融领域依靠线性方程和系统进行预算和投资组合分析,而工程师可以使用相同的工具进行结构分析,以模拟建筑物中的力和应力。线性代数无处不在;每个人都可以在某种程度上欣赏它。
三、线性方程
线性方程是具有一个或多个变量的方程,对于每个变量,变量的指数必须为 2。它可以写成以下形式:a₁x₁ + a₂x₂ + ... + <>rxr = b。值 [a₁, a₁, ..., ar] 和 b 称为线性方程的系数。
线性方程的示例包括:2 x + 5 y = 10、6 x = 18、7v + 8w + 0 x + 2y + 3z = 15,以及 3 x₁ + 4x₂ + 5x₃+9x₄ + 10x₇ = 3。
线性方程的非示例是 2x² + 6x + 5 = 2;这是二次方程*的一个实例。另一个这样的非示例可能是 7x₁ + 3 x₂ = x₁* y₁; 当你绘制这个方程时,其原因变得很明显,它可以重新排列以形成有理函数 y = 7 x /x - 3,它是弯曲 的而不是线性的。
考虑线性方程 2x + 5y = 10。下图说明了线性方程的图形表示,您会注意到它是一条线。当调用直线的方程时,这一点变得更加明显:y = mx + b,其中 m = 斜率和 b = y 截距。线性方程可以如下图所示重新排列以采用这种形式。
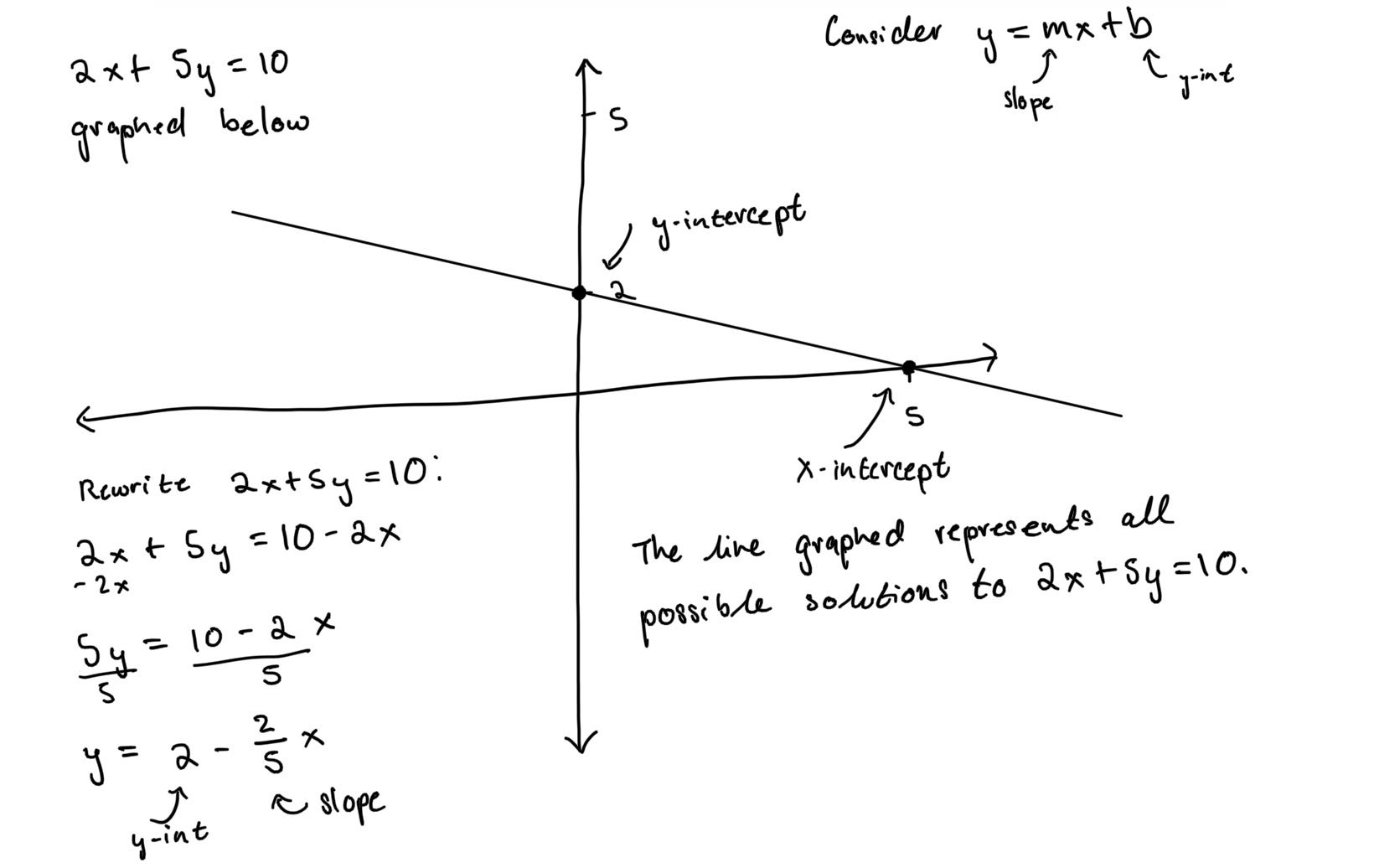
可以得出以下结论:落在直线上的所有 (x, y) 点都是方程 2x + 5y = 10 的解。例如,假设我们选择 x 截距的点 (5, 0),并将 x 和 y 值代入方程中各自的位置。2(5) + 5(0) = 10。线上的任何 (x, y) 点都可以代入方程中,并且相等性将成立。我们可以将这一发现概括为一个规则:
具有两个变量 ax + by = c 的线性方程的 R²* 中的解集可以表示为一条线。
请注意,这个奇异方程有无限数量的解,跨越 R²;稍后我们将仔细研究解决方案的数量。
相同的基本概念转移到表示为 Rⁿ 的高维坐标空间,例如 R³,其中由于添加了第三个变量,直线成为平面。
四、线性方程组
线性方程组是一个或多个线性方程的集合,这些方程共享相似的变量。举个例子:
6x + 2y = 4
2x + 4y = 8
线性方程组的解定义为值(s₁,s₂,...,sr),当替换每个方程各自的变量时,这些值使每个方程为真。在上述系统的情况下,解将是(0,2),因为当(0,2)被替换到系统中时,两个方程的计算结果都是真的。
五、线性系统的解决方案
线性系统解的图形含义是什么?线性系统的解决方案数有哪些不同情况?本节将更详细地研究三种可能性中的每一种。它们如下:
- 独特的解决方案
- 没有解决方案
- 无限解决方案
唯一解决方案:对于具有两个变量(如上述变量)的线性系统,解决方案是交叉点。为什么?解是有序对,其中两个方程都必须满足,如果不存在这样的有序对,那一定意味着直线永远不会相交。这是一个独特解决方案的示例。只有一个解可以满足线性系统中的所有方程。
没有解决方案:考虑没有解决方案的情况。在具有两个变量的线性系统的上下文中,这可能意味着什么?在什么情况下,一组行永远不会相遇?一种情况是,如果它们是平行的。对于所有直线都平行的线性系统,线性系统将没有解。另一种情况是,虽然某些线可能与其他线相交,但没有一条所有线共享的共同交点。
无限解:线性系统的最终情况是存在无限解。什么时候有可能为双变量线性系统提供无限解?如果线相同,则存在无限的交点,因为它们重叠,因此存在无限解。考虑以下线性系统:
6x + 3y = 18
2x + y = 6
虽然系数可能不同,但这些线实际上是相同的!如果将第一个方程的每个系数除以 3,则得到的方程将为 2x + y = 6。
线性系统解数的可视化随着变量数量的增加而变化。下图是具有三个变量的线性系统的所有三个解案例的可能图。三维之后的任何东西都变得难以想象,但同样的规则适用!无论有多少变量,所有线性系统要么没有解,要么只有一个解,要么有无限解。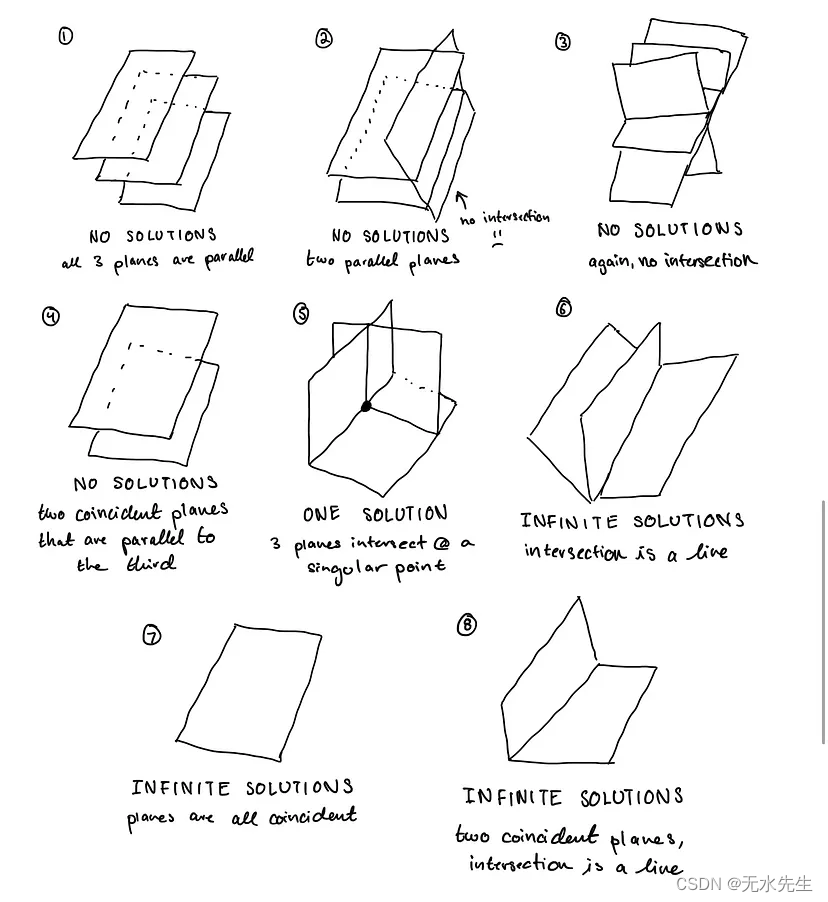
此图改编自 src。
六、矩阵表示法
随着线性方程变得越来越复杂,符号可能会变得笨拙。将线性系统的信息压缩为易于操作和使用非常重要,因此矩阵符号通常用于一组方程。系数矩阵是一种从每个方程中排除 b 系数的矩阵。增强矩阵包含 b 系数,因此它比系数矩阵多一列。

矩阵的大小(也称为顺序)告诉我们矩阵有多少行和列。m x n 矩阵是包含 m 行和 n 列的矩阵。行数对应于系统有多少个线性方程,而列数告诉我们有多少变量。注意确保行数在列数之前,因为顺序不可互换。
七、求解线性系统
有一种系统的方法可以确定线性系统是否有解,如果有,它是否有唯一的解或无限解,并从那里获得解。求解线性系统可以使用原始形式的线性方程或矩阵来执行,但建议使用矩阵,因为符号更清晰、更紧凑。然而,熟悉这两种方法是件好事,因为它们提供了对另一种方法机制的额外见解。
下面是解决无矩阵方程组的逐步过程。基本思想是通过将预先存在的方程相乘来创建新方程,以获得相同的方程,然后可以从另一个方程中添加或减去以消除一个变量。然后重复这个过程,直到我们从系统中消除了足够多的未知数,以便能够解决一个变量,然后通过反向替换来求解其余变量。最后,需要进行检查以确保解实际上满足方程组。

八、行操作
前面概述的步骤可以转移到以矩阵为中心的求解线性系统的过程。记下每次转换后如何在矩阵中指定消除的变量。但是,在我们开始之前,让我们定义一些行操作。两个实际上与我们之前应用的操作并行。
- 替换:“将一行替换为其自身和另一行的总和。*
- 交换:“交换两行。*
- 缩放:“将一行中的所有条目乘以非零常量。*
让我们再次重新接近相同的线性系统,但这次使用矩阵并应用行运算。
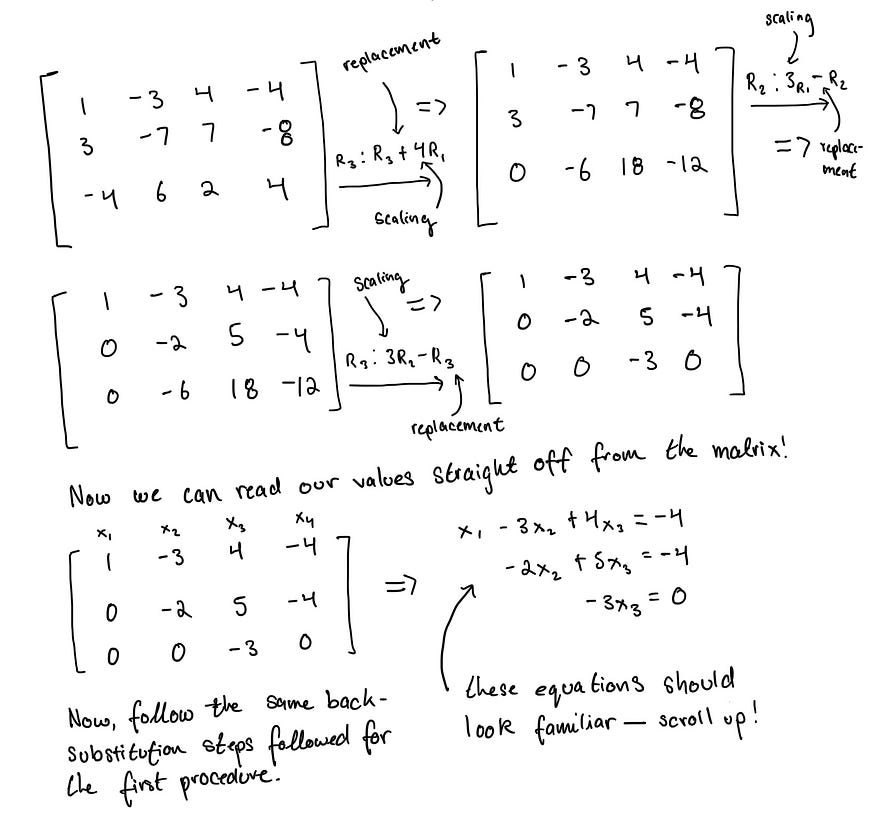
请注意,我使用了与线性方程方法完全相同的运算和比例因子。不出所料,我们最终得到了与以前相同的方程。其他需要注意的是最终矩阵左下角的三角形。这种模式的出现是有意义的,因为 0 是消除变量的标记,每个消除的变量都使我们更接近于确定可以轻松求解的方程;这反过来又使整个系统的解决方案取得进展。我们将重新审视这种情况,我将在下一章中为它提供一个更正式的定义。
九、总结
在本章中,我们学习了:
- 线性方程:具有一个或多个变量的方程,其中方程的次数必须等于 1。
- 线性方程组:线性方程组的集合。
- 一个或多个线性方程组的解:线性系统要么没有解,要么有唯一的解,要么有无限的解。
- 矩阵表示法:矩形数组,用作表示线性系统的压缩方式。
- 行操作:替换、交换和缩放操作允许我们将矩阵转换为已消除足够多的未知变量来为系统求解的矩阵。
- 求解线性系统:一种系统的方法,用于查找 a) 给定线性系统是否存在解,以及 b) 如果存在解,它们的确切值是多少。
参考资料:
Linear Algebra 1: Linear Equations and Systems | by tenzin migmar (t9nz) | Sep, 2023 | Towards Data Science (medium.com)