【论文基本信息】
标题：Fast identification of fluorescent components in three-dimensional excitation-emission matrix fluorescence spectra via deep learning
标题译名：通过深度学习快速识别 三维激发-发射矩阵荧光光谱中的荧光组分
期刊与年份：Chemical Engineering Journal 2022
作者机构：河海大学环境学院
原文：https://www.sciencedirect.com/science/article/pii/S1385894721044685

报告时间：2023年1月

0 摘要

• 三维激发发射矩阵（Three-dimensional excitation-emission matrix，3D-EEM）荧光光谱技术已广泛应用于从天然水体到废水处理过程中的样品的荧光组分检测。
• （在检测前，）需要（使用）平行因子分析(PARAFAC)等数据解释方法来分解3D-EEM光谱中重叠的荧光信号。
• 然而，PARAFAC对数据的严格要求和复杂的程序限制了样品的在线监测和分析。
• 本文开发了一个基于深度学习方法的快速荧光识别网络(FFI-Net)模型，通过简单地输入单个3D-EEM光谱来快速预测荧光成分的数量和光谱。
• 训练了两种卷积神经网络(CNN)对荧光成分的数量进行分类，准确率为0.956；对荧光组分的光谱进行预测，最小平均绝对误差为8.9 × 10^-4。
• 本文证明了，当训练数据集可以使用更多的3D-EEM数据时，FFI-Net模型的准确性将进一步提高。
• 同时，（我们）设计了人性化的界面，便于实际应用。
• 我们的方法为克服PARAFAC的不足提供了一种强大的方法，并为水样中荧光成分的在线分析提供了一个新的平台。

1 介绍

1.1 三维荧光技术

各种微生物分泌的胞外聚合物质(EPS)和可溶性微生物产物(SMP)广泛存在于污水（生物处理过程）和自然水环境中。

根据以往的研究，EPS和SMP的主要成分都是多糖、蛋白质、腐殖质和DNA。

其中腐殖酸、木质素、芳香族氨基酸、DNA等均具有荧光，可通过荧光光谱技术检测。当这些荧光组分在溶液中的种类和浓度发生变化时，3D-EEM荧光光谱检测到的荧光位置和荧光强度也会发生相应的变化。

因此，3D-EEM荧光光谱已被公认为识别和跟踪自然水生环境和废水中荧光组分的有效工具。

1.2 3D-EEM的经典解析方法

然而，原始3D-EEM数据由数千个激发/发射(Ex/Em)对和相应的荧光强度值组成。由于三维eem光谱中存在大量的干扰噪声和重叠的荧光信息，因此需要采用经济高效且准确的解析方法来提取和分析实测的三维eem光谱中的有用信息。

为了从3D-EEM光谱中挖掘有意义的信息，已经提出了几种可行的方法，包括荧光区域积分、主成分分析、平行因子分析(PARAFAC)。

其中，PARAFAC模型作为一种多路方法，越来越多地被用于将3D-EEM光谱分解为底层荧光组分。PARAFAC不仅可以估计3D-EEM光谱中荧光团的数量，还可以提供每种荧光物质的相对浓度。

然而，原来的PARAFAC分析程序是复杂和耗时的。同时，PARAFAC需要大量相关的3D-EEM光谱来保证成分分类的准确性。这些问题限制了PARAFAC对荧光团的快速分析和鉴定。

1.3 PARAFAC与ML的结合现状

随着人工智能的快速发展，PARAFAC模型已经与多种机器学习方法结合，用于对3D-EEM光谱进行分析，如人工神经网络、自组织映射(SOM)等。例如，Cuss等人使用了四种机器学习方法(决策树、k-最近邻、多层感知器和支持向量机)根据PARAFAC的分析结果对荧光成分的来源进行分类。

但是，这些分析过程和方法仍然需要经历PARAFAC的主要步骤(数据预处理、离群值检验、分半验证等)。换句话说，克服PARAFAC缺点(即耗时和严格的数据要求)的ML方法仍然缺失。

3D-EEM光谱的组成：激发波长×发射波长×荧光强度。灰度图像数据的组成：高度×宽度×灰度值。二者在结构上相同。卷积神经网络是ML中一种处理图像数据的强大方法，然而其在3D-EEM光谱荧光组分分析和识别中的应用尚未被提出。

本文开发了一个连续的CNN-CNN架构模型，称为快速荧光识别网络(fast fluorescent identification network，FFI- Net)模型，用于快速识别单个3D- EEM光谱中的荧光组分。

在预训练的CNN-CNN模型的帮助下，只需加载单个3D-EEM光谱，FFI-Net模型便可以快速提供荧光组分的数量以及每个荧光组分的图像。通过这种方式，FFI-Net模型可以提供标准化的描述能力，并实现诸如废水在线分析和各种水体的快速监测等应用。

2 材料与方法

2.1 样本采集

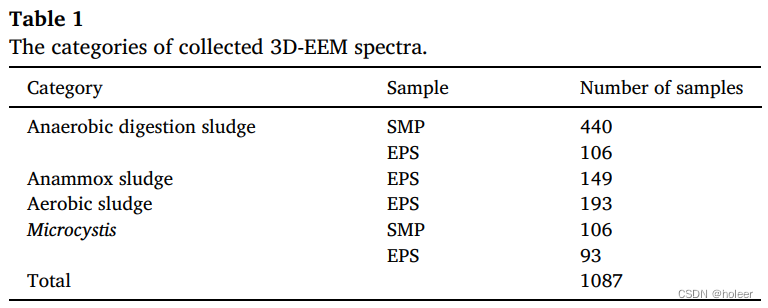
本文使用的数据是来自不同实验的EPS和SMP样本，如下表所示。其中有一小部分来自作者之前发表的工作，而大部分3D-EEM光谱来自作者未发表的工作。

2.2 荧光测量与数据预处理

这些3D-EEM光谱具有不同的数据结构，即不同的Ex和Em波长范围以及Ex和Em间隔，如下图所示。

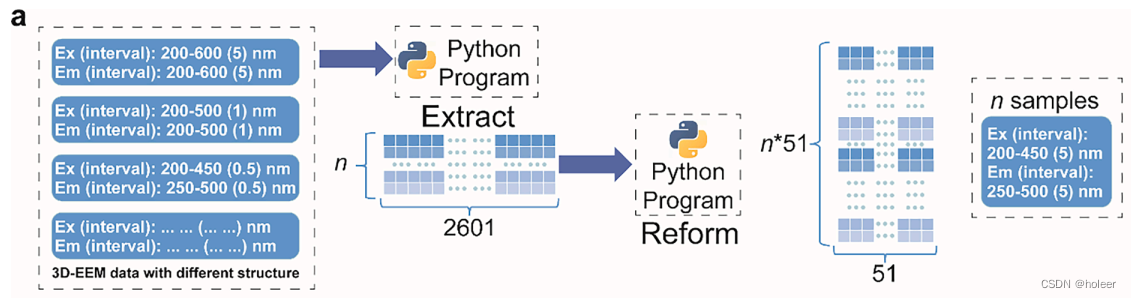
为了便于PARAFAC分析和后续模拟，作者用程序对不同结构的3D-EEM光谱进行了预处理，以形成相同尺寸的光谱。（尺寸如下表所示，51*51=2601，每一行一个光谱）

属性	最小值	最大值	步长	采样数
Ex	200	450	5	51
Em	250	500	5	51

然后，使用另一个程序将这些每一行数据重塑为矩阵形式(n*51 × 51)，适用于PARAFAC分析。

2.3 平行因子方法

使用Matlab的DOMFluor工具箱进行PARAFAC分析，如公式1所示。

$$x_{ijk}=\sum _{f=1}^F{a}_{if}{b}_{jf}{c}_{kf}+e_{ijk}(1)$$

• 等号左边：第i个样品在激发波长k和发射波长j处的荧光发射
• 等号右边第一项：PARAFAC分量之和，每个分量f是三个值的积：丰度(aif)、第f发射光谱的最小二乘估计(bjf)和激发光谱的最小二乘估计(ckf)
• 等号右边第二项：一个残差矩阵。

2.4 基于深度卷积神经网络的FFI-Net模型的建立

模型如下图所示。

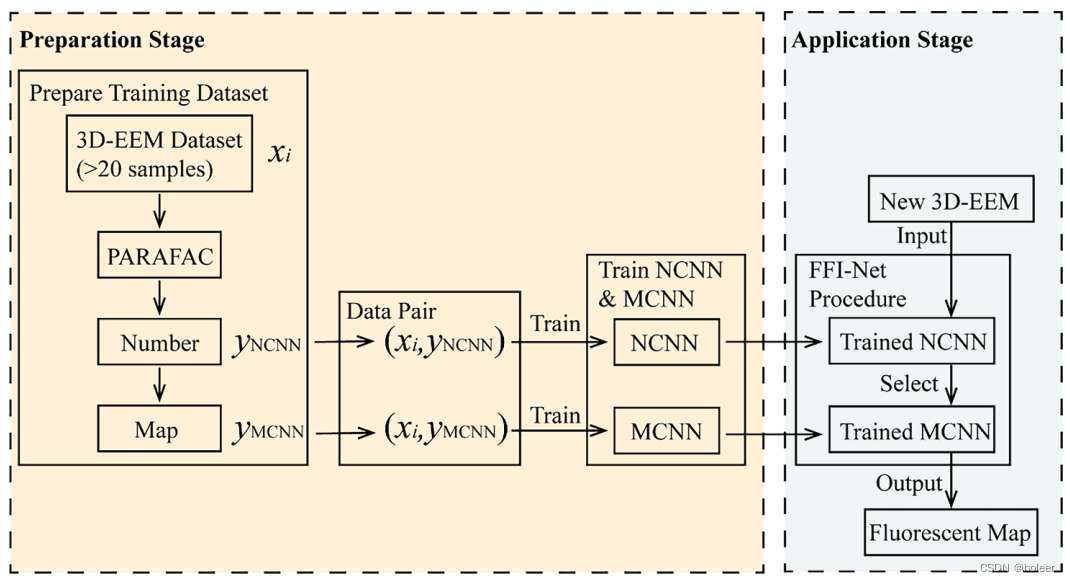
图2：FFI-Net模型的建立。在准备阶段，用PARAFAC对3D-EEM数据集xi进行分析，形成荧光组分的数量yNCNN和这些荧光组分的图谱yMCNN。然后使用数据对(xi, yNCNN)和数据对(xi, yMCNN)分别训练NCNN和MCNN。

MCNN-n模型包含n个具有相同结构的CNN模型，每个CNN模型基于输入的3D-EEM光谱预测一个荧光组分。

图3a：NCNN模型是为分类任务设计的。

输出：分类标签，代表荧光组分的数量。可能的取值有3、4、5，分别用one-hot编码表示为0、1和2。

输入：取某一3D-EEM光谱的Ex和Em波长作为像素位置，设置各Ex/Em处的荧光强度为通道值，这样就将3D-EEM光谱数据变换为图像数据（高×宽×通道=51×51×1）。

主要组成部分：两个二维卷积层和两个二维最大池化层。

损失函数：分类交叉熵。

（性能评价：十倍交叉验证）

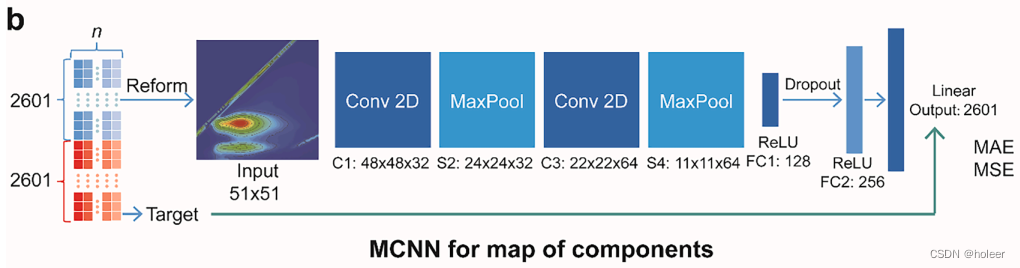
图3b：MCNN模型用于预测样本中每个组分的图谱。

输入：与NCNN模型的输入相同

输出：为2601个分量的荧光强度，可以转化为高度×宽度×通道= 51 × 51 × 1的分量图。

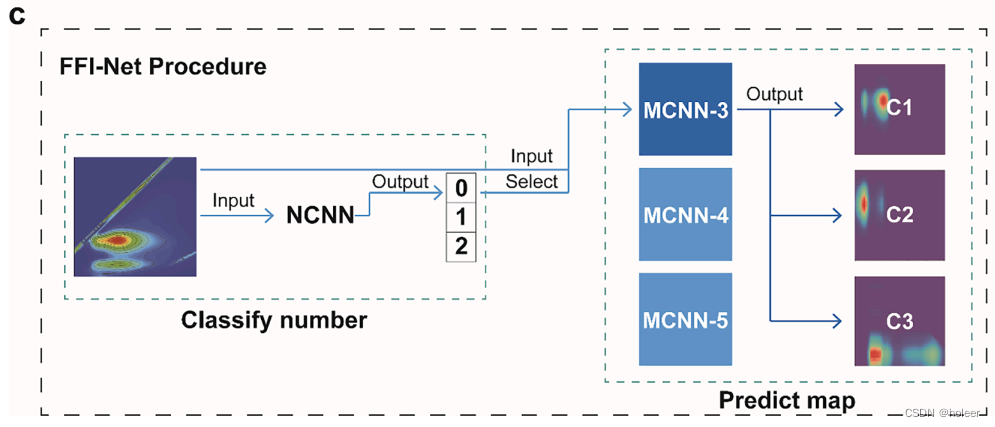
下图是FFI-Net模型工作的一个例子：首先将一个3D-EEM光谱输入到预训练的NCNN中，输出荧光组分的数量。这里输出0，对应3种，然后将图谱输入到预训练的MCNN-3中，输出三种荧光组分的图谱。

2.5 软件

FFI-Net的用户界面使用PyQt5开发，如下图所示。

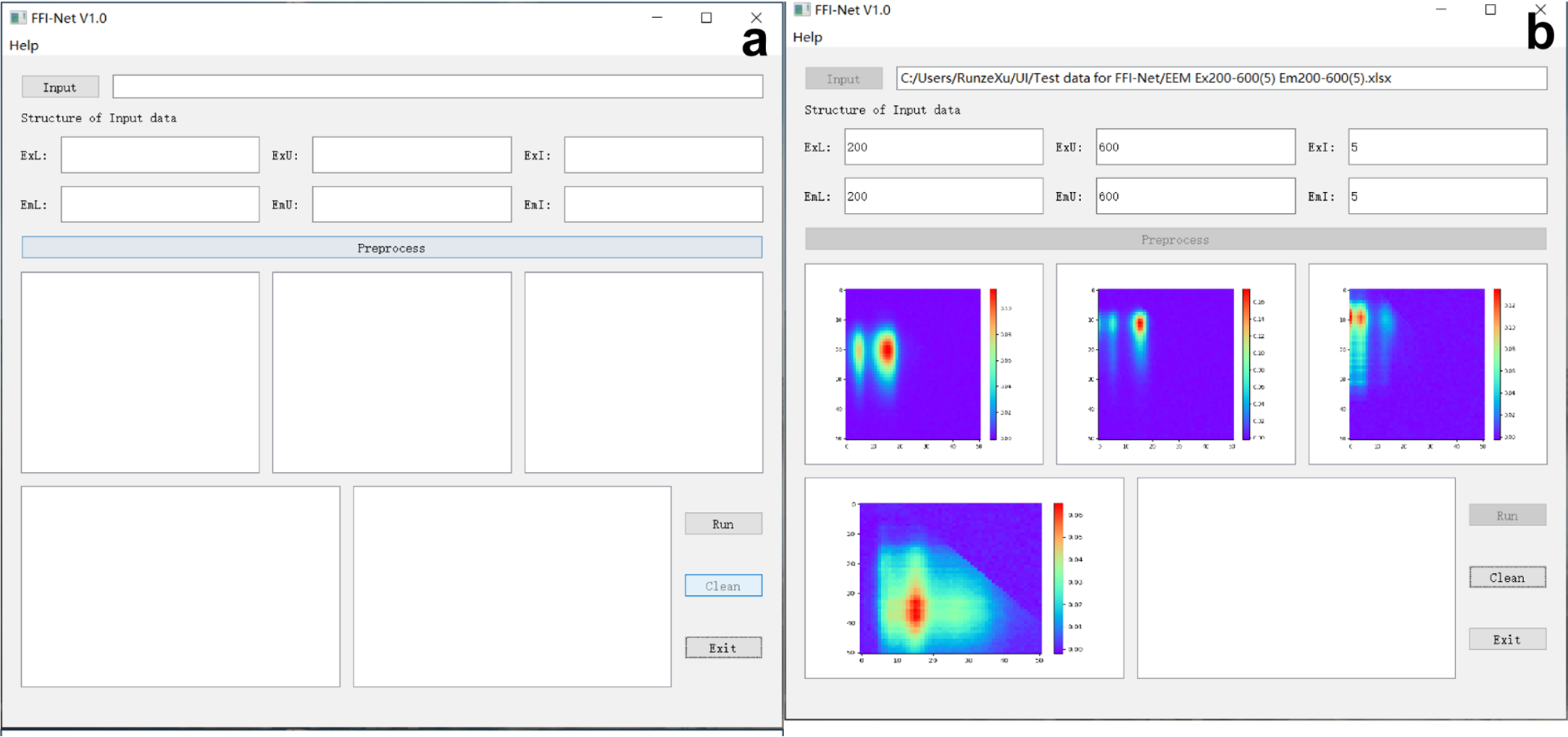
注意：输入数据需要满足预处理程序的要求。

3 结果与讨论

3.1 3D-EEM数据的特征

由于不同类别的样品收集的实验不同，同一类别的3D-EEM光谱可能具有不同的荧光峰和强度。

由于不同微生物分泌的荧光团不同，整个数据集的荧光信息很丰富。

3.2 使用平行因子法生成数据集

将数据集按照荧光组分数量归类，得到3个子集：3个荧光组分(D3)、4个荧光组分(D4)和5个荧光组分(D5)。每个分类数据集中的3D-EEM数量是不平衡的：D3、D4和D5分别有584、237和266个3D-EEM光谱。为了减少对D3的隐式偏向，将D4和D5中的3D-EEM光谱重复一次，这样D3、D4和D5分别为584、474和532。

3.3 FFI-Net模型的训练与评估

NCNN模型在10次运行中对测试数据集的平均损失和精度分别达到0.116和0.956。该结果表明，NCNN模型可以准确地分类3D-EEM光谱中荧光组分的数量。

值得注意的是，MCNN-n模型包含n个具有相同结构的CNN模型，每个CNN模型基于输入的3D-EEM光谱预测一个荧光组分。根据PARAFAC的结果，n的值可以分别设置为3、4或5。因此，我们分别在MCNN-3、MCNN-4和MCNN-5中集成了所有CNN模型的性能，所有MCNN模型都具有较低的测试MAE（平均绝对误差）和MSE（均方误差），如下表所示。这些结果表明，MCNN的训练是有效的。

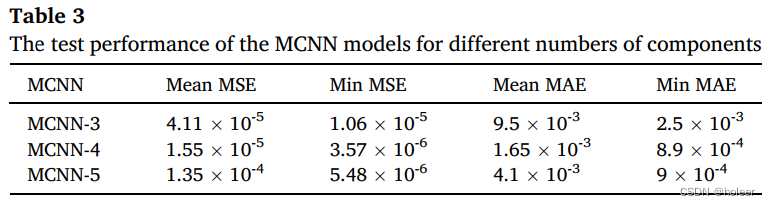
为了直观地突出MCNN的功能，我们从D3中随机抽取了一个样本，并用D3中的剩余样本训练了MCNN-3模型。标准PARAFAC结果和模型输出结果的对比如下图所示。可以看到，二者几乎是相同的。

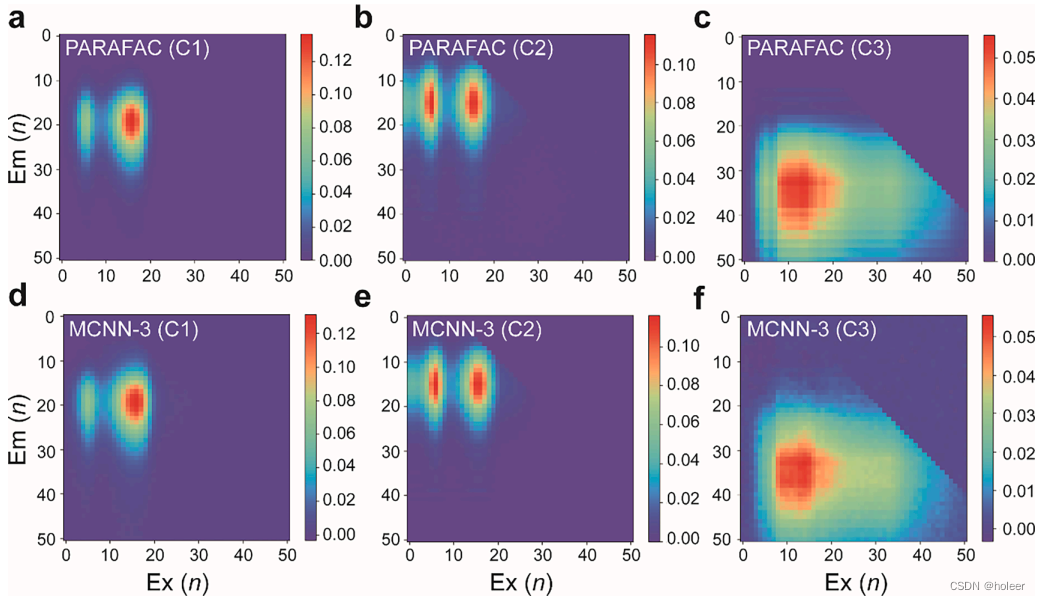
由此可验证模型的有效性。

3.4 使用未见的3D-EEM光谱评估FFI-Net模型

三个未见数据集中的荧光组分如下表所示。

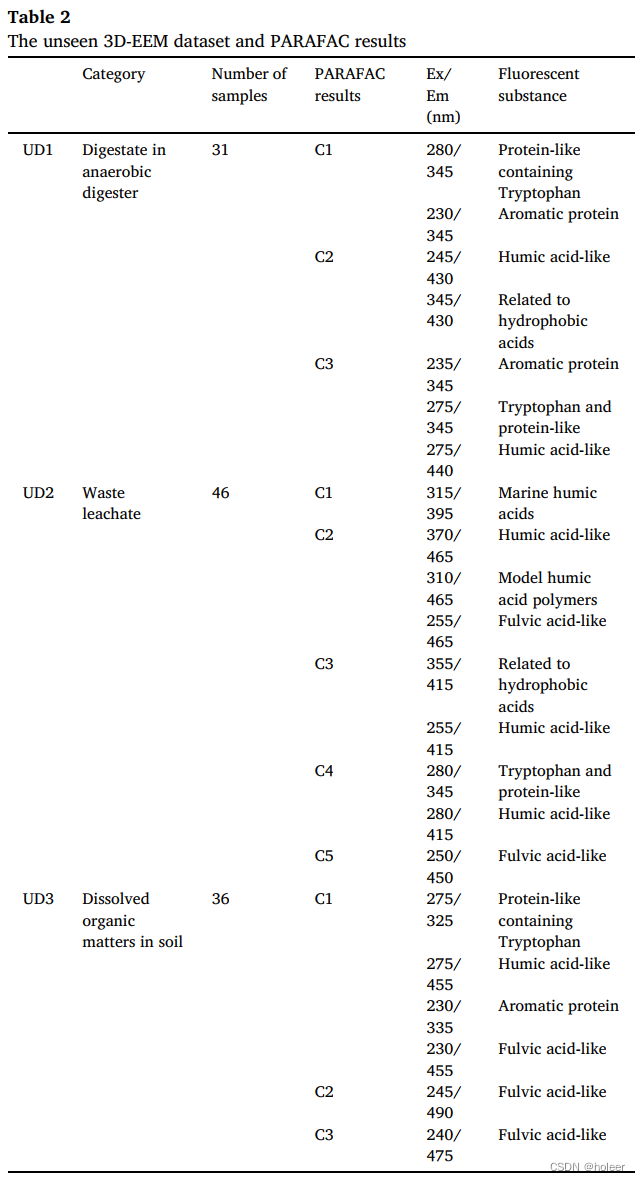
这些未见过的3D-EEM数据集首先由PARAFAC分析，形成荧光组分的数据进行比较。

在用未见数据集测试模型之前，我们使用NCNN和MCNN中表现出较高准确性的原始数据集(1590个样本)训练建立的FFI-Net模型(表3)。然后，使用原始数据集训练的NCNN和MCNN分析三个未见数据集中的样本(表4)。训练的NCNN对UD1表现出较高的准确性(100%)，不能很好地分类UD2的荧光组分数量（这可能是由于UD2中腐殖质组分复杂，与原始数据集中富含微生物产物的样品有很大差异；样本没有输入到训练好的MCNN中，因为NCNN的错误结果会导致MCNN的完全错误结果），对于UD3显示出可接受的预测准确性(86%)，而MCNN生成的荧光图与标准答案不相同。原始数据集训练的FFI-Net对UD2和UD3的预测结果较差，因为UD2和UD3的荧光模式不包括在原始数据集中。

为了测试FFI-Net是否能记住更多的荧光模式，我们使用了额外的NCNN和MCNN样本（除了待分析的目标样本之外的未看的样本）。在UD2和UD3的所有样本中，使用额外数据集训练的NCNN和MCNN进行有序测试。使用新数据集训练NCNN后，UD2和UD3样本的NCNN准确率提高到100%。同时，使用新数据集训练的MCNN对UD2 (5.5 × 10-4)和UD3 (9.3 × 10-4)的MAE都很低。这与原始数据集训练的MCNN的良好测试性能是一致的(表3)。这些结果表明，在训练数据集中增加具有新的荧光模式的样本可以大大提高FFI-Net对于特定荧光模式的性能。因此，通过将包含更多荧光图案的新数据整合到训练数据集中，可以不断提高FFI-Net的应用范围和准确性。

3.5 FFI-Net模型与平行因子法的比较

作者将本文的方法的过程与PARAFAC的过程进行了比较，发现FFI-Net模型的分析速度比PARAFAC快得多，如下表所示。

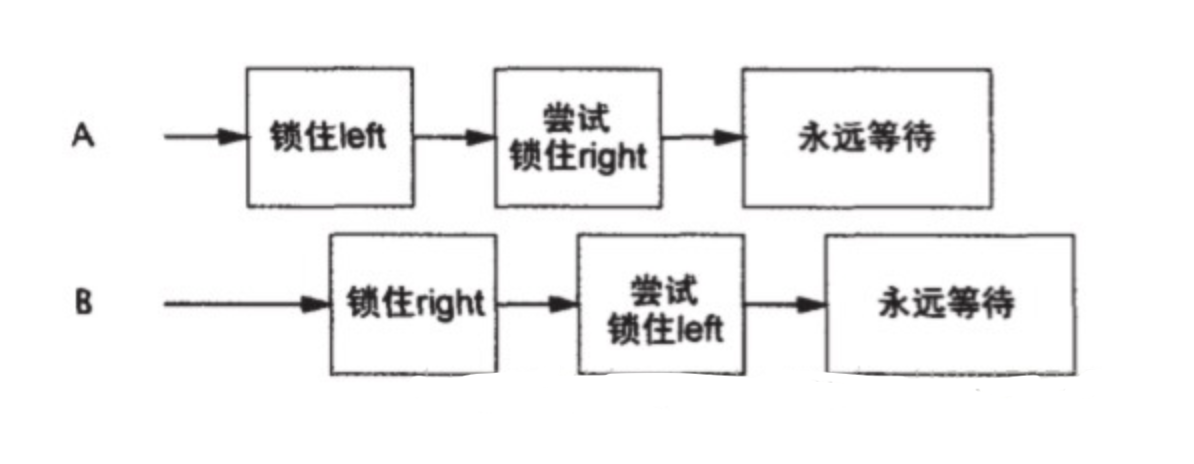
PARAFAC具有多步分析过程(如下图所示)，由于模型验证过程[19]的要求，通常更适合对20-100个样本进行联合分析。

如果FFI-Net模型实现良好，FFI-Net模型的计算时间小于1 min。FFI-Net模型具有分析速度快、样品要求简单等优点，优于PARAFAC方法。

因此，本研究开发的FFI-Net模型可以嵌入基于到PARAFAC的监测系统中，取代PARAFAC的功能。为了准确模拟其光谱中的荧光组分，需要根据其光谱和相应的PARAFAC结果建立新的训练数据集。

总体而言，FFI-Net模型分析速度快(小于1 min)，数据需求低(一个样本)，为在线监测系统在废水处理、饮用水处理和地表水中的应用开辟了道路。

4 结论

这项工作开发了一种简单而准确的深度学习方法来快速预测3D- EEM光谱中重叠的荧光组分。

我们证明，经过良好训练的FFI-Net模型可以通过只输入单个样本来快速预测3D-EEM光谱中的荧光成分，克服了PARAFAC的缺陷(耗时的程序和严格的数据要求)。

随着荧光数据可用性的增加，FFI-Net模型的准确性可以进一步提高。

总的来说，这项工作为实时分析荧光3D-EEM数据开辟了一条新的途径，这将使废水在线分析和水环境的快速监测成为可能。