数据结构----算法–五大基本算法(这里没有写分支限界法)和银行家算法
一.贪心算法
1.什么是贪心算法
在有多个选择的时候不考虑长远的情况,只考虑眼前的这一步,在眼前这一步选择当前的最好的方案
二.分治法
1.分治的概念
分治法:分而治之
将一个问题拆解成若干个解决方式完全相同的问题
满足分治的四个条件
1.问题难度随着数据规模缩小而降低
2.问题可拆分
3.子问题间相互独立
4.子问题的解可合并
2.典型的分治:二分查找(折半搜索) BinaryChop
前提:有序
时间复杂度O(log2的n次方)
1.循环实现二分查找
//循环
int BinaryChop1(int a[], int begin, int end ,int find) {if (a == nullptr || begin > end) return -1;while (begin<= end) {int mid = begin+(end- begin)/2 ;if (a[mid] == find) {cout << "找到了,返回在数组中的下标" << endl;return mid;}else if (a[mid] < find) {begin = mid + 1;}else if (a[mid] > find) {end = mid - 1;}}return -1;
}
2.递归实现二分查找
//递归
int BinaryChop2(int a[], int begin, int end, int find) {if (a == nullptr || begin > end) return -1;int mid = begin+(end- begin)/2;if (a[mid] == find) {cout << "找到了,返回数组下标" << endl;return mid;}else if (a[mid] < find) {begin = mid + 1;}else if (a[mid] > find) {end = mid - 1;}return BinaryChop2(a, begin, end, find);}
三.回溯法
1.回溯法解决的问题
1.求子集的问题
2.求排列的问题
3.求集合的问题
4.求棋盘的问题
2.回溯常见的写法
循环嵌套递归
3.用回溯法解决一道全排列的问题(此题的网址为https://leetcode.cn/problems/permutations/)
此题在之前的博客中具体分析过(博客的网址如下https://blog.csdn.net/m0_73483024/article/details/133589061?spm=1001.2014.3001.5502)
题目:
四.动态规划(Dynamic Programming)
1.动态规划可以解决的问题
动态规划可以用来求最优解(最大、最小、最多等)的问题
2.动态规划操作对象所要满足的性质
大问题可以拆解成解决方案完全相同的子问题,并且要满足以下两个性质
1.满足最优子结构性质(子问题的最优解构成当前问题的最优解)
2.无后效性(一旦某一状态被确定,那么过去这个状态如何求得的我们就再也不关注了)
3.动态规划的求解过程
1.拆分
2.定状态(子问题的最优解)
3.做决策
4.求状态转移方程
4.动态规划的实现手段
1.自顶向下带备忘的解法(大到小)
2.自底向上的解法(小到大)
注意:动态规划的空间消耗是用来换时间了
5.关于动态规划的问题
1.凑钱问题
题目:
有1元,3元,5元面额的钞票,想要凑到n元钱
解决方法:
创建一个f数组
f(n)表示想要凑到n元钱所需要的最小的钞票数
我们观察下面式子,找出规律
f(0)=0
f(1)=f(1-1)+1=1
f(2)=f(2-1)+1=2
f(3)=min{f(3-3)+1=1,f(3-1)+1=3}=1
f(4)=min{f(4-3)+1=2,f(4-1)+1=2}=2
f(5)=min{f(5-5)+1=1,f(5-3)+1=3,f(5-1)+1=3}=1
推导出动态转移方程得
f(i)=min{f(i-v[j])}+1(v[j]<=i)
这里v是一个存1元,3元,5元面额的钞票的数组,j是遍历v数组的变量
2.一维的动态划分问题:最长递增子序列(LIS)
题目:
有一个数组中有6、3、9、8、4、7、2、5、10、1这些元素,找到这个数组中的最长递增子序列
解决方法:
方法一
创建一个f数组
f(n)表示n下标与前序元素构成的LIS的长度
我们观察下面式子,找出规律
f(0)=1
f(1)=1
f(2)=max{9>3 f(1)+1=2
9>6 f(0)+1=2
1(只有自己本身,长度为1)
}=2
f(3)=max{8>3 f(1)+1=2
8>6 f(0)+1=2
1(只有自己本身,长度为1)
}=2
f(4)=max{4>3 f(1)+1=2
1(只有自己本身,长度为1)
}=2
f(5)=max{7>4 f(4)+1=3
7>3 f(1)+1=2
7>6 f(0)+1=2
1(只有自己本身,长度为1)
}=3
推导出动态转移方程得
f(i)=max(f(j)+1,1) (v[j]<v[i],0<=j<i)
这里v是数组,i和j是遍历v数组的变量
方法二(相较于方法一优化)
创建一个数组用来存等长LIS右边界的最小值(下标当作长度)
从左到右遍历数组,对创建的数组进行更新,最后数组的使用量就是最长递增子序列的长度
看下面进行理解
f(0)=1
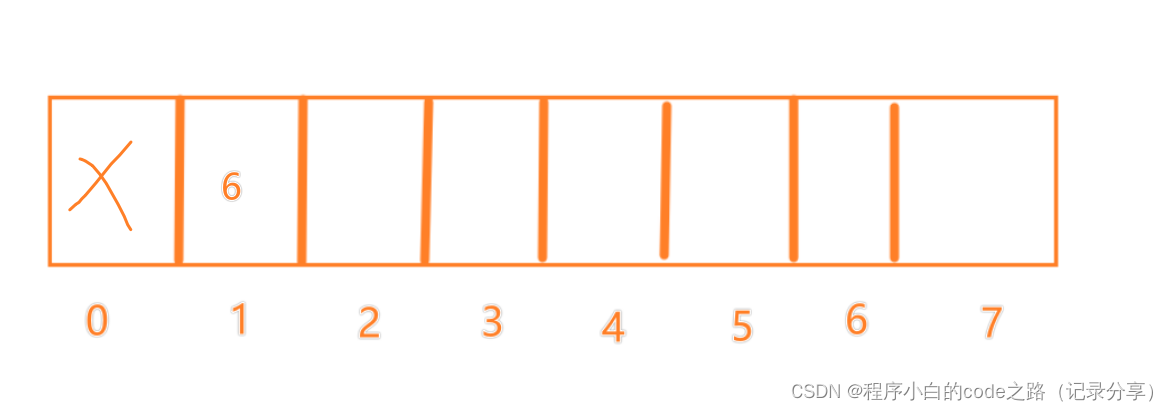
f(1)=1
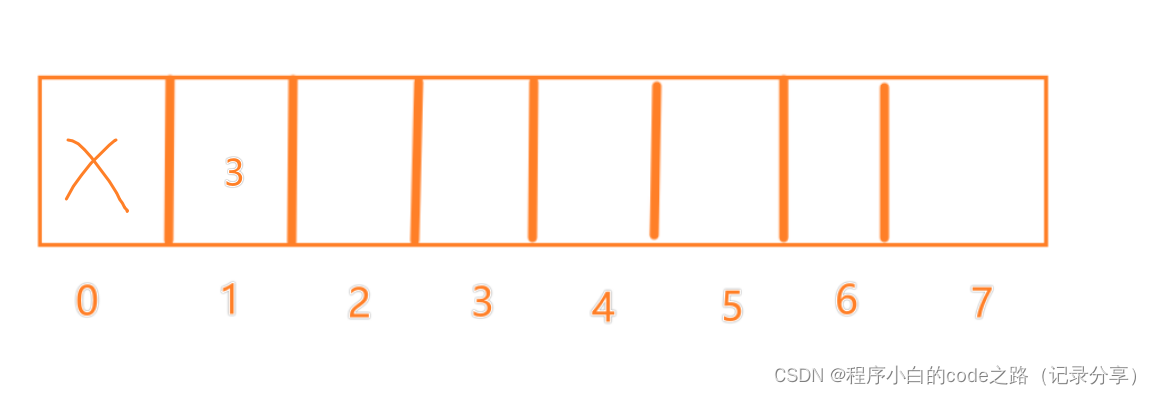
f(2)=2
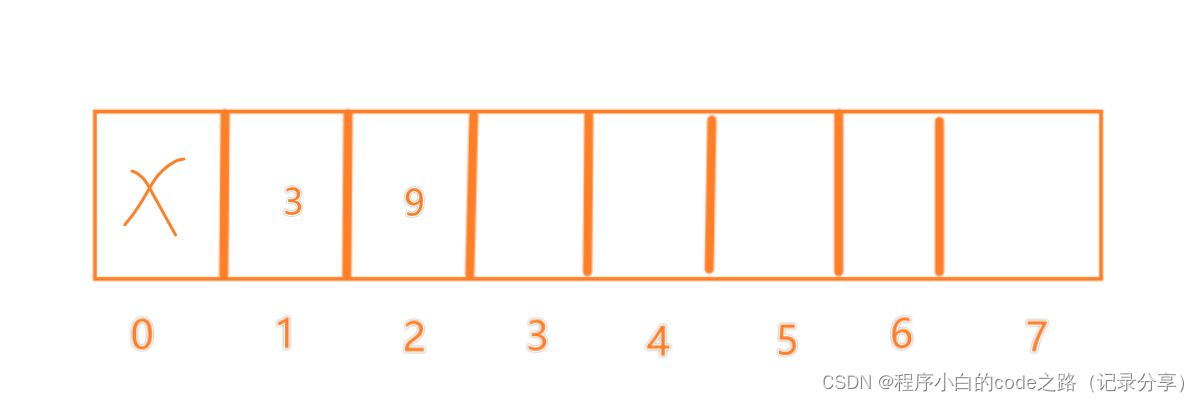
f(3)=2
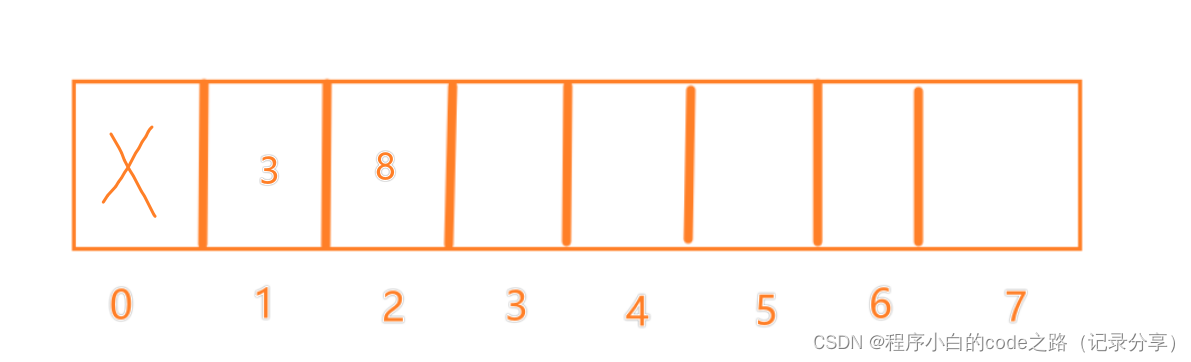
f(4)=2
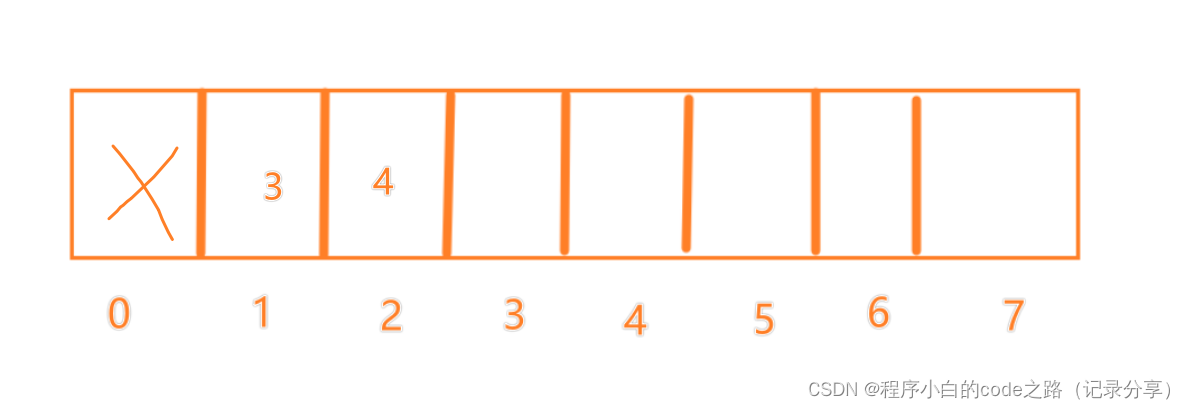
f(5)=3
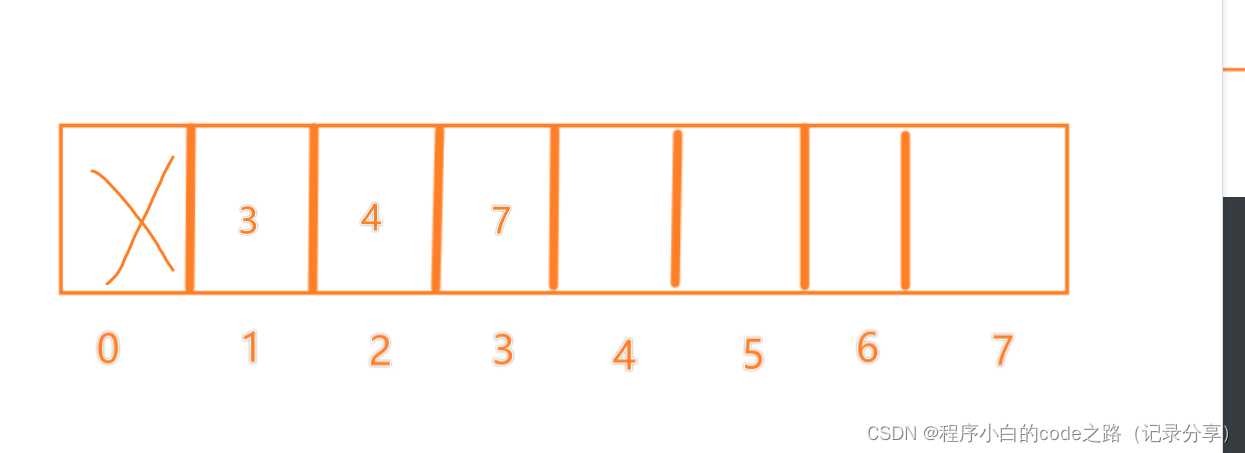
下面的过程就不再写了
方法三(在方法二的基础上,进行二分搜索,在进行数组的更新时使用二分搜索)
3.二维的动态规划问题:捡苹果
题目:
有一个m*n的格子,每个格子中有数量不一的苹果,一个小机器人(只能往右或者往下走)从左上角走到它不能再走了,求它最多能捡到多少个苹果
解决:
状态转移方程为 c[i] [j]=max{c[i-1] [j],c[i] [j-1]}+A[i] [j]
c数组存的是到每个位置所能捡到的最大苹果数量,A数组存的是每个位置的苹果数量
4.二维的动态规划问题且带附加条件的:最长公共子序列(LCS)
题目:
求X数组{A,B,B,D,C,B,C}与Y数组{B,C,D,B,A,C}的最长公共子序列
解决:
状态转移方程为 c[i] [j]={c[i-1] [j-1]+1 xi==yi
max{c[i-1] [j],c[i] [j-1]}} xi!=yi
}
c数组存的是x数组走到数组中的某个元素和y数组走到数组中的某个元素时,二者所构成的LCS的长度
c[i] [j]存的是x数组走到第i个元素,y数组走到第j个元素,二者所构成的LCS的长度
四.博弈树
1.博弈树(Game Tree)
棋类中用到的博弈树满足的条件
1.二者零和
2.全信息
3.非偶然
注意:博弈树要在时间消耗和结果准确度中做一个平衡
2.极大极小搜索树(是在原有博弈树的基础上实现的)
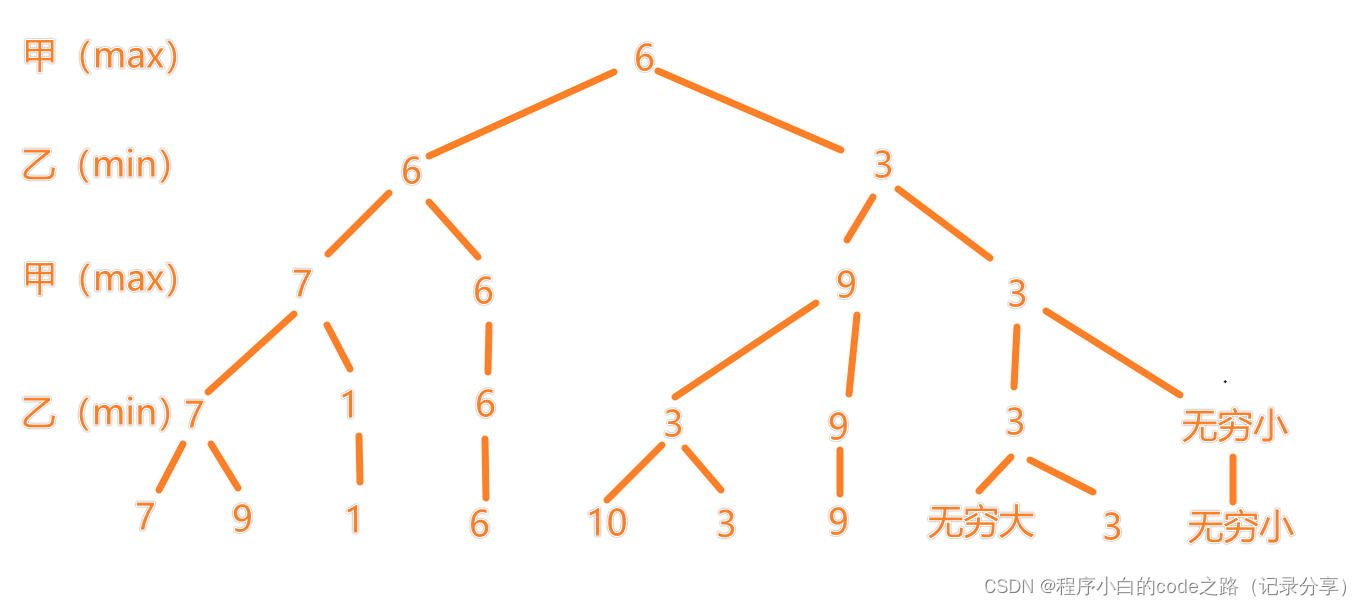
看下面这张图理解博弈树
甲是自己要选择尽量大的
乙是对手要使我们最小,所以乙选择尽量小的
3.α-β剪枝(对极大极小树的优化)
看下面图片(都是部分图,不是完整的)理解α-β剪枝
图片一
注意:这是一个深搜过程(图中数字表示处理的步骤)
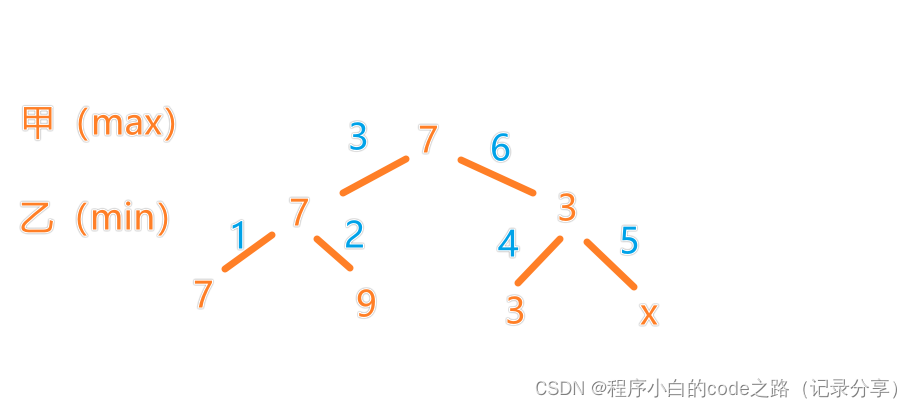
当此图第4步得到的值小于第3步得到的值,那么第5步就不用处理了
图片二
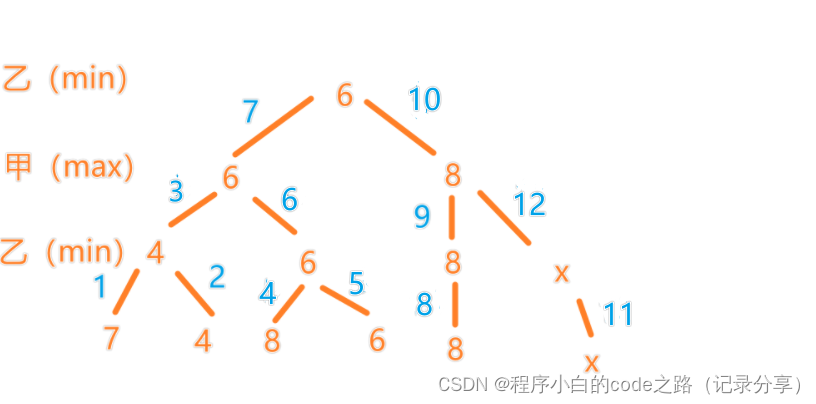
注意:这是一个深搜过程(图中数字表示处理的步骤)
当此图第9步得到的值大于第7步得到的值,那么第11步和第12步就不用处理了
五.银行家算法
1.使用银行家算法要满足的条件
1.固定数量的进程共享固定数量的资源
2.进程最大请求资源数
3.单次申请的资源数不能超出可分配资源数
4.不是一次性全部申请,分批次进行
5.进程等待资源的时间是有限的(不会无休止等待)
6.当满足进程的最大资源需求,进程应该在有限时间内归还资源
2.银行家算法的操作步骤
A:总资产
B:所需的最大资源数
C:已经分配的资源数
D:仍然需要的资源数
E:每次请求的资源数
F:可分配的资源数
1.看E<=F是否满足
如果不满足就等待
如果满足就进行下一步
2.看E<=D是否满足
如果不满足,失败
如果满足就进行下一步
3.假装分配,更新各个值
C=C+E
D=D-E
F=F-E