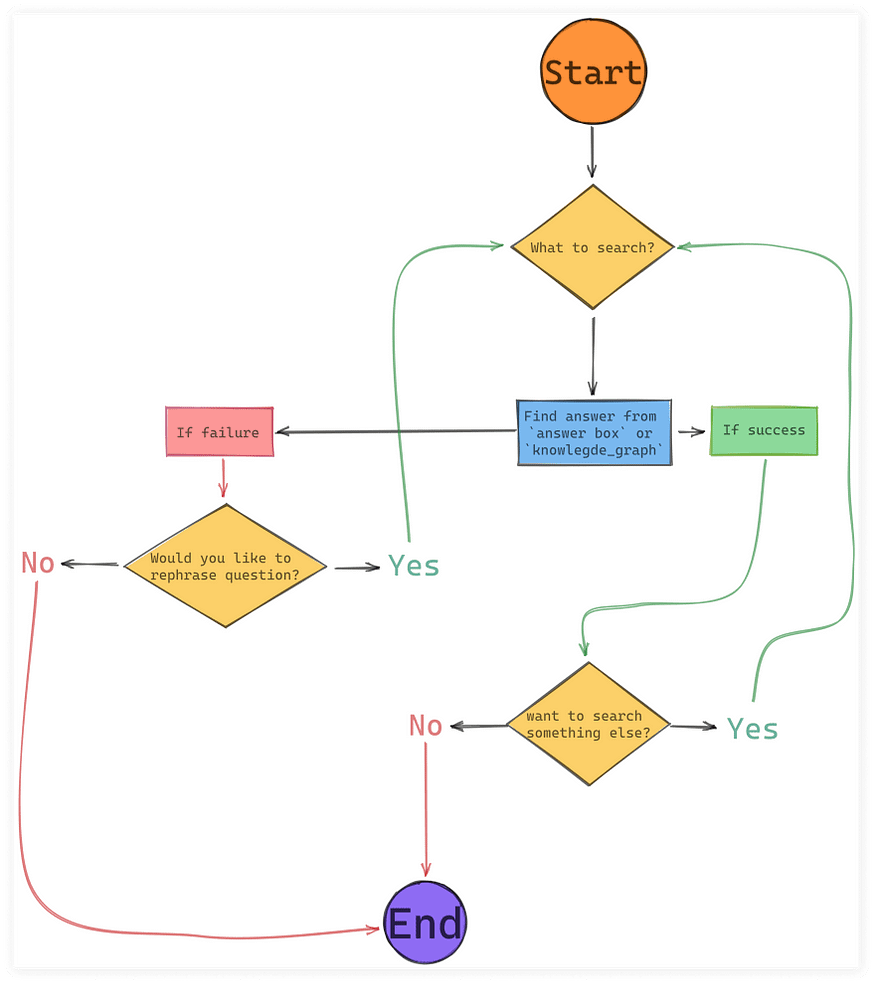
Self-attention介绍
Self-attention是一种特殊的attention,是应用在transformer中最重要的结构之一。attention机制,它能够帮助找到子序列和全局的attention的关系,也就是找到权重值wi。Self-attention相对于attention的变化,其实就是寻找权重值的wi过程不同。
- 为了能够产生输出的向量yi,self-attention其实是对所有的输入做了一个加权平均的操作,这个公式和上面的attention是一致的。
- j代表整个序列的长度,并且j个权重的相加之和等于1。值得一提的是,这里的 wij并不是一个需要神经网络学习的参数,它是来源于xi和xj的之间的计算的结果(这里wij的计算发生了变化)。它们之间最简单的一种计算方式,就是使用点积的方式。
xi和xj是一对输入和输出。对于下一个输出的向量yi+1,有一个全新的输入序列和一个不同的权重值。
- 这个点积的输出的取值范围在负无穷和正无穷之间,所以要使用一个softmax把它映射到[0,1] 之间,并且要确保它们对于整个序列而言的和为1。
- 以上这些就是self-attention最基本的操作。
Self-attention和Attention使用方法
根据他们之间的重要区别,可以区分在不同任务中的使用方法:
- 在神经网络中,通常来说会有输入层(input),应用激活函数后的输出层(output),在RNN当中会有状态(state)。如果attention (AT) 被应用在某一层的话,它更多的是被应用在输出或者是状态层上,而当使用self-attention(SA),这种注意力的机制更多的实在关注input上。
- Attention (AT) 经常被应用在从编码器(encoder)转换到解码器(decoder)。比如说,解码器的神经元会接受一些AT从编码层生成的输入信息。在这种情况下,AT连接的是**两个不同的组件**(component),编码器和解码器。但是如果用**SA**,它就不是关注的两个组件,它只是在关注应用的**那一个组件**。那这里就不会去关注解码器了,就比如说在Bert中,使用的情况,就没有解码器。
- SA可以在一个模型当中被多次的、独立的使用(比如说在Transformer中,使用了18次;在Bert当中使用12次)。但是,AT在一个模型当中经常只是被使用一次,并且起到连接两个组件的作用。
- SA比较擅长在一个序列当中,寻找不同部分之间的关系。比如说,在词法分析的过程中,能够帮助去理解不同词之间的关系。AT却更擅长寻找两个序列之间的关系,比如说在翻译任务当中,原始的文本和翻译后的文本。这里也要注意,在翻译任务重,SA也很擅长,比如说Transformer。
- AT可以连接两种不同的模态,比如说图片和文字。SA更多的是被应用在同一种模态上,但是如果一定要使用SA来做的话,也可以将不同的模态组合成一个序列,再使用SA。
- 其实有时候大部分情况,SA这种结构更加的general,在很多任务作为降维、特征表示、特征交叉等功能尝试着应用,很多时候效果都不错。
Self-attetion实现步骤
- 这里实现的注意力机制是现在比较流行的点积相乘的注意力机制
- self-attention机制的实现步骤
- 第一步: 准备输入
- 第二步: 初始化参数
- 第三步: 获取key,query和value
- 第四步: 给input1计算attention score
- 第五步: 计算softmax
- 第六步: 给value乘上score
- 第七步: 给value加权求和获取output1
- 第八步: 重复步骤4-7,获取output2,output3
1. 准备输入
# 这里随机设置三个输入, 每个输入的维度是一个4维向量
import torch
x = [[1, 0, 1, 0], # Input 1[0, 2, 0, 2], # Input 2[1, 1, 1, 1] # Input 3
]
x = torch.tensor(x, dtype=torch.float32)2. 初始化参数
# 每一个输入都有三个表示,分别为key(橙黄色),query(红色),value(紫色)。
# 每一个表示,希望是一个3维的向量。由于输入是4维,所以参数矩阵为 4*3 维。# 为了能够获取这些表示,每一个输入(绿色)要和key,query和value相乘
# 在例子中,使用如下的方式初始化这些参数。
w_key = [[0, 0, 1],[1, 1, 0],[0, 1, 0],[1, 1, 0]
]
w_query = [[1, 0, 1],[1, 0, 0],[0, 0, 1],[0, 1, 1]
]
w_value = [[0, 2, 0],[0, 3, 0],[1, 0, 3],[1, 1, 0]
]
w_key = torch.tensor(w_key, dtype=torch.float32)
w_query = torch.tensor(w_query, dtype=torch.float32)
w_value = torch.tensor(w_value, dtype=torch.float32)print("w_key: \n", w_key)
print("w_query: \n", w_query)
print("w_value: \n", w_value)3. 获取key,query和value
# 使用向量化获取keys的值
[0, 0, 1]
[1, 0, 1, 0] [1, 1, 0] [0, 1, 1]
[0, 2, 0, 2] x [0, 1, 0] = [4, 4, 0]
[1, 1, 1, 1] [1, 1, 0] [2, 3, 1]# 使用向量化获取values的值
[0, 2, 0]
[1, 0, 1, 0] [0, 3, 0] [1, 2, 3]
[0, 2, 0, 2] x [1, 0, 3] = [2, 8, 0]
[1, 1, 1, 1] [1, 1, 0] [2, 6, 3]# 使用向量化获取querys的值
[1, 0, 1]
[1, 0, 1, 0] [1, 0, 0] [1, 0, 2]
[0, 2, 0, 2] x [0, 0, 1] = [2, 2, 2]
[1, 1, 1, 1] [0, 1, 1] [2, 1, 3]
# 将query key value分别进行计算
keys = x @ w_key
querys = x @ w_query
values = x @ w_value
print("Keys: \n", keys)
print("Querys: \n", querys)
print("Values: \n", values)
4. 给input1计算attention score
# 获取input1的attention score,使用点乘来处理所有的key和query,包括自己的key和value。
# 这样就能够得到3个key的表示(因为有3个输入),就获得了3个attention score(蓝色)
[0, 4, 2]
[1, 0, 2] x [1, 4, 3] = [2, 4, 4]
[1, 0, 1]# 注意: 这里只用input1举例。其他的输入的query和input1做相同的操作.
attn_scores = querys @ keys.T
print(attn_scores)5. 计算softmax
from torch.nn.functional import softmaxattn_scores_softmax = softmax(attn_scores, dim=-1)
print(attn_scores_softmax)
attn_scores_softmax = [[0.0, 0.5, 0.5],[0.0, 1.0, 0.0],[0.0, 0.9, 0.1]
]
attn_scores_softmax = torch.tensor(attn_scores_softmax)
print(attn_scores_softmax)softmax([2, 4, 4]) = [0.0, 0.5, 0.5]6. 给value乘上score
使用经过softmax后的attention score乘以它对应的value值(紫色),这样就得到了3个weighted values(黄色)
1: 0.0 * [1, 2, 3] = [0.0, 0.0, 0.0]
2: 0.5 * [2, 8, 0] = [1.0, 4.0, 0.0]
3: 0.5 * [2, 6, 3] = [1.0, 3.0, 1.5]
weighted_values = values[:,None] * attn_scores_softmax.T[:,:,None]
print(weighted_values)7. 给value加权求和获取output1
把所有的weighted values(黄色)进行element-wise的相加。
[0.0, 0.0, 0.0]
+ [1.0, 4.0, 0.0]
+ [1.0, 3.0, 1.5]
------------------------
= [2.0, 7.0, 1.5]
得到结果向量[2.0, 7.0, 1.5](深绿色)就是ouput1的和其他key交互的query representation
8. 重复步骤4-7,获取output2,output3
outputs = weighted_values.sum(dim=0)
print(outputs)