文章目录
- 多源最短路径--Floyd-Warshall算法
- 1. 算法思想
- 2. dist数组和pPath数组的变化
- 3. 代码实现
- 4. 测试观察
- 5. 源码
前面的两篇文章我们学习了两个求解单源最短路径的算法——Dijkstra算法和Bellman-Ford算法
这两个算法都是用来求解图的单源最短路径的算法,区别在于Dijkstra算法不能求解带负权路径的图,而Bellman-Ford算法可以求解带负权路径的图,当然如果图中存在负权回路(负权环)的情况,种情况是求不出最短路径的!Bellman-Ford算法也无能为力,不过我们可以对负权回路的情况进行判定。
那这篇文章我们要再来学习一个求解多源最短路径的算法——Floyd-Warshall算法
那在前面介绍最短路径的问题的时候就已经给大家解释了什么是单源最短路径,什么是多源最短路径,我们再来回顾一下:
单源最短路径指的是从一个源节点出发,计算到其他所有节点的最短路径。也就是说,在单源最短路径问题中,只需要确定一个起点,然后计算该起点到图中所有其他节点的最短距离。
多源最短路径则是在图中计算任意两个节点之间的最短路径。换言之,需要求解所有可能的起点和终点之间的最短路径。
多源最短路径–Floyd-Warshall算法
Floyd-Warshall算法是一种解决多源最短路径问题(任意两点间的最短路径)的算法。
Floyd算法又称为插点法,是一种利用动态规划的思想寻找给定的加权图中多源点之间最短路径的算法(可以求解带负权的图)。
该算法名称以创始人之一、1978年图灵奖获得者、斯坦福大学计算机科学系教授罗伯特·弗洛伊德命名。
当然:
我们前面学的Dijkstra算法和Bellman-Ford算法,它们是用来求单源最短路径的,但是我们如果以所有的顶点为起点都走一遍Dijkstra/Bellman-Ford算法的话,其实也可以得到任意两点间的最短距离。
不过呢,Dijkstra算法的话不可以求解带负权路径的图,而Bellman-Ford算法呢效率又有点低。
1. 算法思想
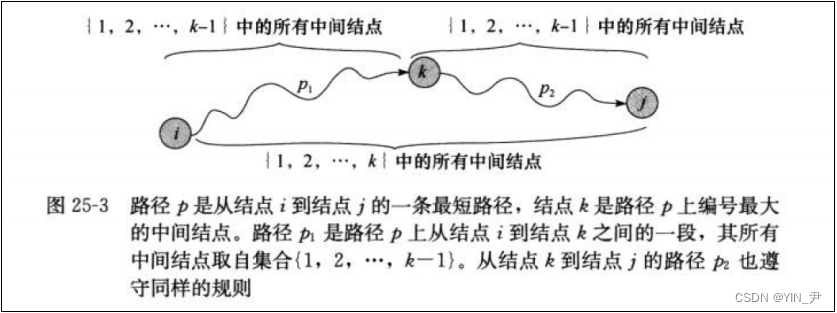
Floyd算法考虑的是一条最短路径的中间节点:
设k是最短路径p的一个中间节点,那么从i到j的最短路径p就被分成i到k和k到j的两段最短路径p1,p2。
p1是从i到k且中间节点属于{1,2,…,k-1}取得的一条最短路径;p2是从k到j且中间节点属于{1,2,…,k-1}取得的一条最短路径
那它这里如何去求i到j(i,j都可以是任意顶点)最短路径p呢?
即Floyd算法本质是三维动态规划,D[i][j][k]表示从点i到点j只经过0到k个点最短路径,然后建立起转移方程,然后通过空间优化,优化掉最后一维度,变成一个最短路径的迭代算法,最后即得到所有点的最短路。
给大家简单解释一下上面原理中的这个公式,在动态规划中应该叫状态转移方程:
Di,j,k表示从i到j的最短路径,该路径经过的中间结点是剩余的结点组成的集合中的结点,假设经过k个结点,编号为1…k,然后这里就分为了两种情况:
- 如果路径经过了结点k,那么
ij的距离就等于ik的距离加上kj的距离,然后剩余就经过k-1个点- 如果不经过结点k,那
ij的距离就等于i到j经过k-1个点(不包括k)的距离
那i到j的最短路径就等于这两种情况中的最小值
2. dist数组和pPath数组的变化
然后呢在Floyd-Warshall算法中,记录最短路径距离(权值)的dist数组和记录路径(该路径经过了哪些点)的pPath数组我们就要做一些变化了:
前面的两个算法中我们的dist数组和pPath数组都是用了一个一维数组就行了。
但是Floyd-Warshall算法就不一样了,因为前两个算法算的是单源最短路径,而Floyd-Warshall算法是多源最短路径。
因为前面我们都是一个起点,然后求其它顶点到起点的最短路径;而现在是多源,即每个顶点都可以是起点,所以我们要记录每个顶点作为起点时到其它顶点的最短路径距离和路径。
那我们就需要用二维数组了。
3. 代码实现
那下面我们就来尝试写一写Floyd-Warshall算法的代码:
首先它就不需要给起点了,因为Floyd-Warshall算法求的是多源最短路径,每个顶点都可能是起点,我们都要求
其次,dist数组和pPath数组这里我们要用二维的(vvDist、vvpPath)
然后
前面的这些初始化工作就不多解释了
接着
我们要把图中所有相连的边的信息直接更新一下,因为上面我们说了那个公式叫做状态转移方程,而这里初始化更新的结果就作为起始状态,后面通过状态转移方程不断更新得到最终结果
那然后下面我们就根据状态转移方程更新就行了
🆗,搞定!
4. 测试观察
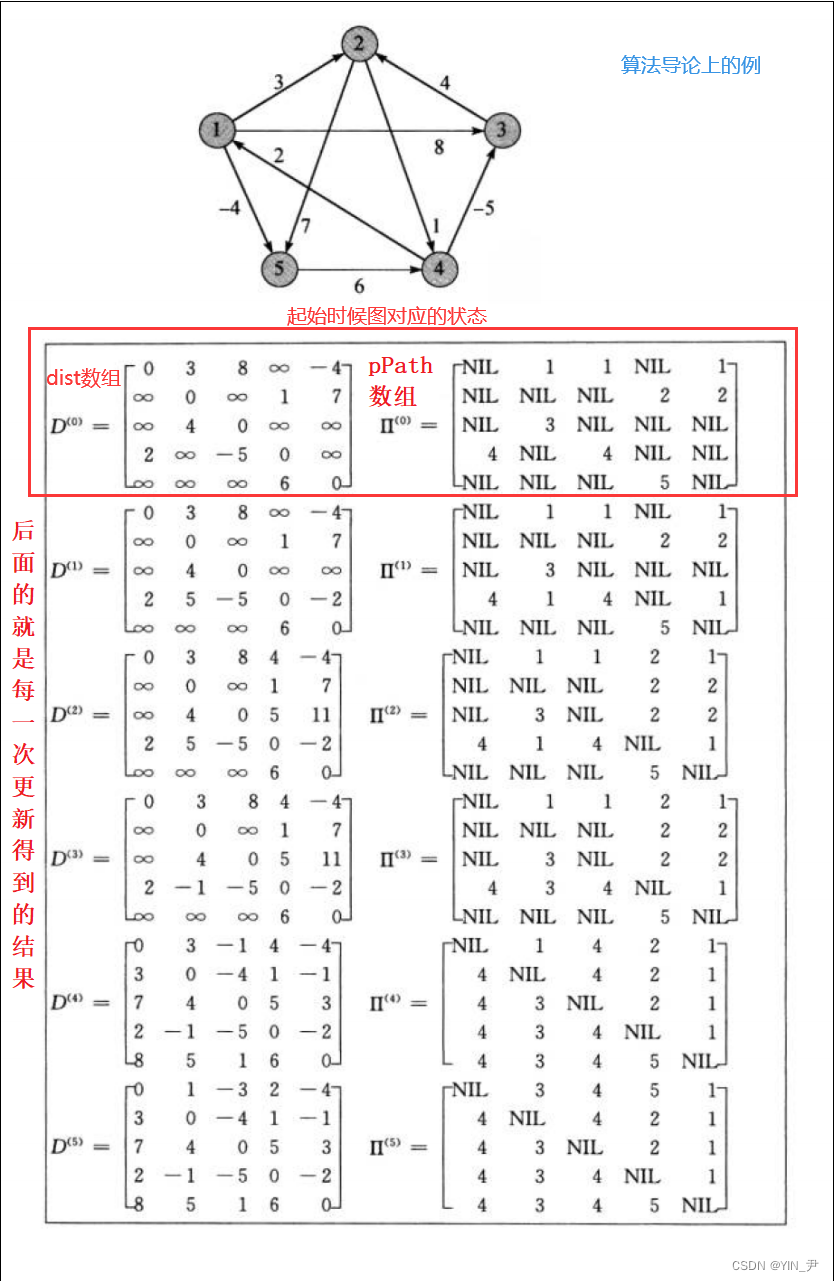
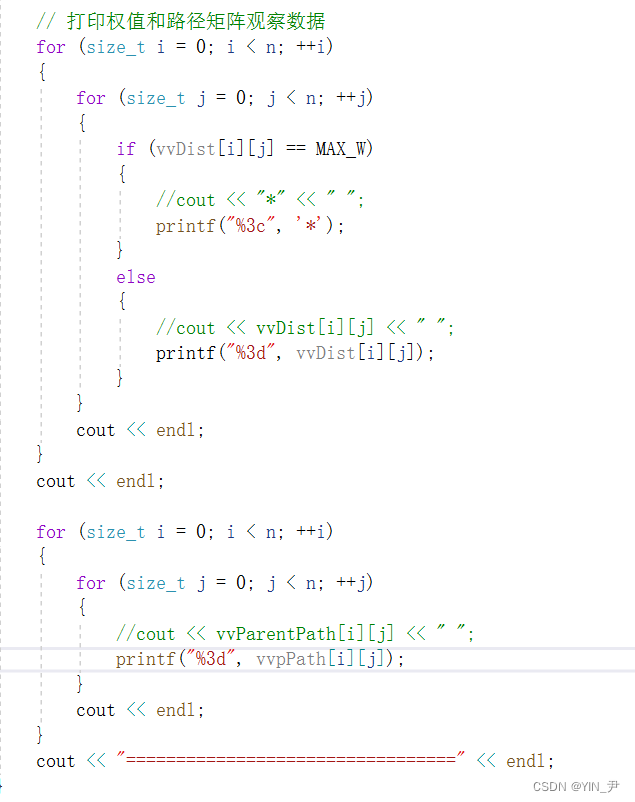
那下面我们再加一个打印权值和路径的二维数组的代码,因为上面那个例子也是把每一步对应的两个二维数组(矩阵)画了出来,我们可以打印(每个顶点作为中间结点更新之后的都打印一下)出来观察对比一下:
这段代码很简单,没什么解释的
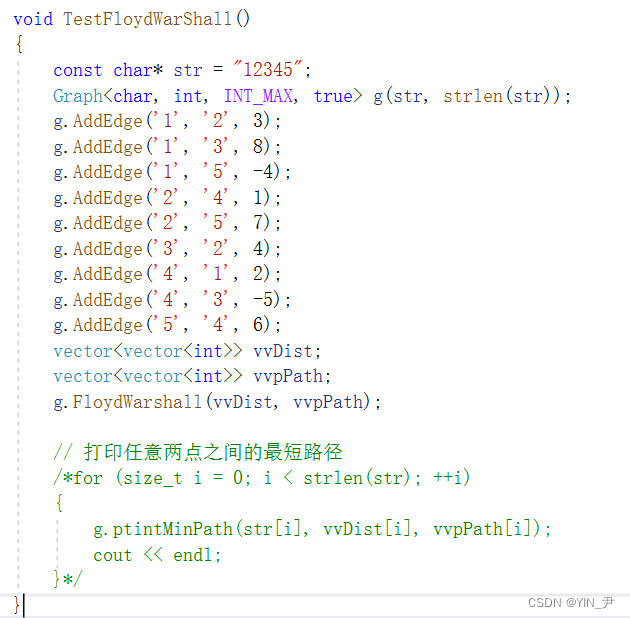
然后我们来测试一下:
这个测试用例就对应上面给大家看的例子中的图
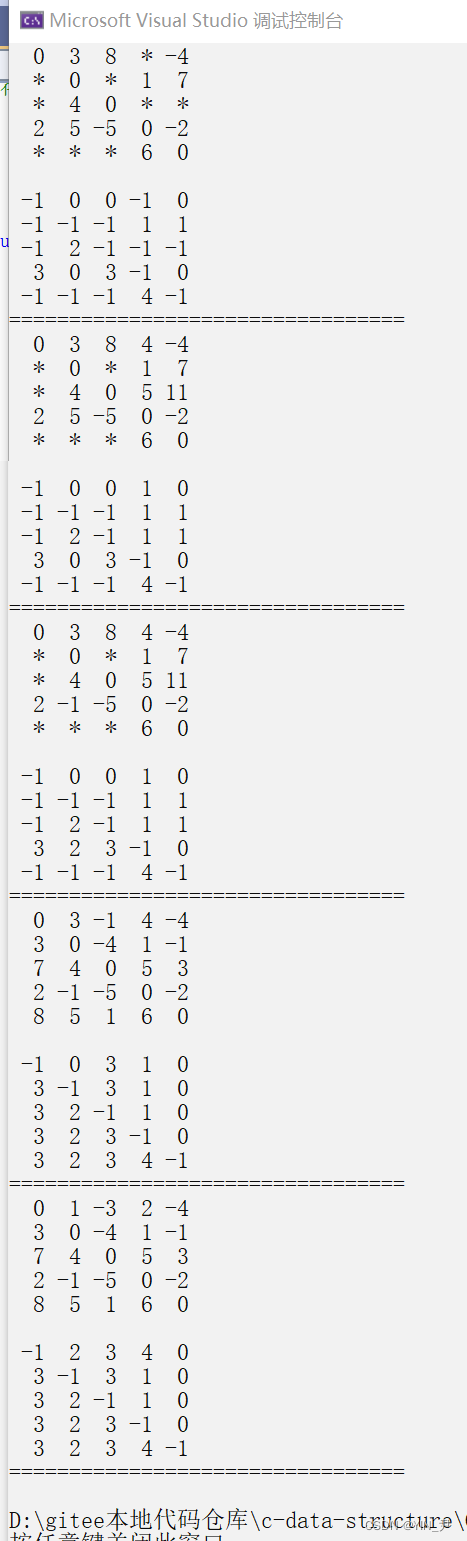
运行一下
当然我们这里不能像他那样横着打印
我可以给大家调整一下:
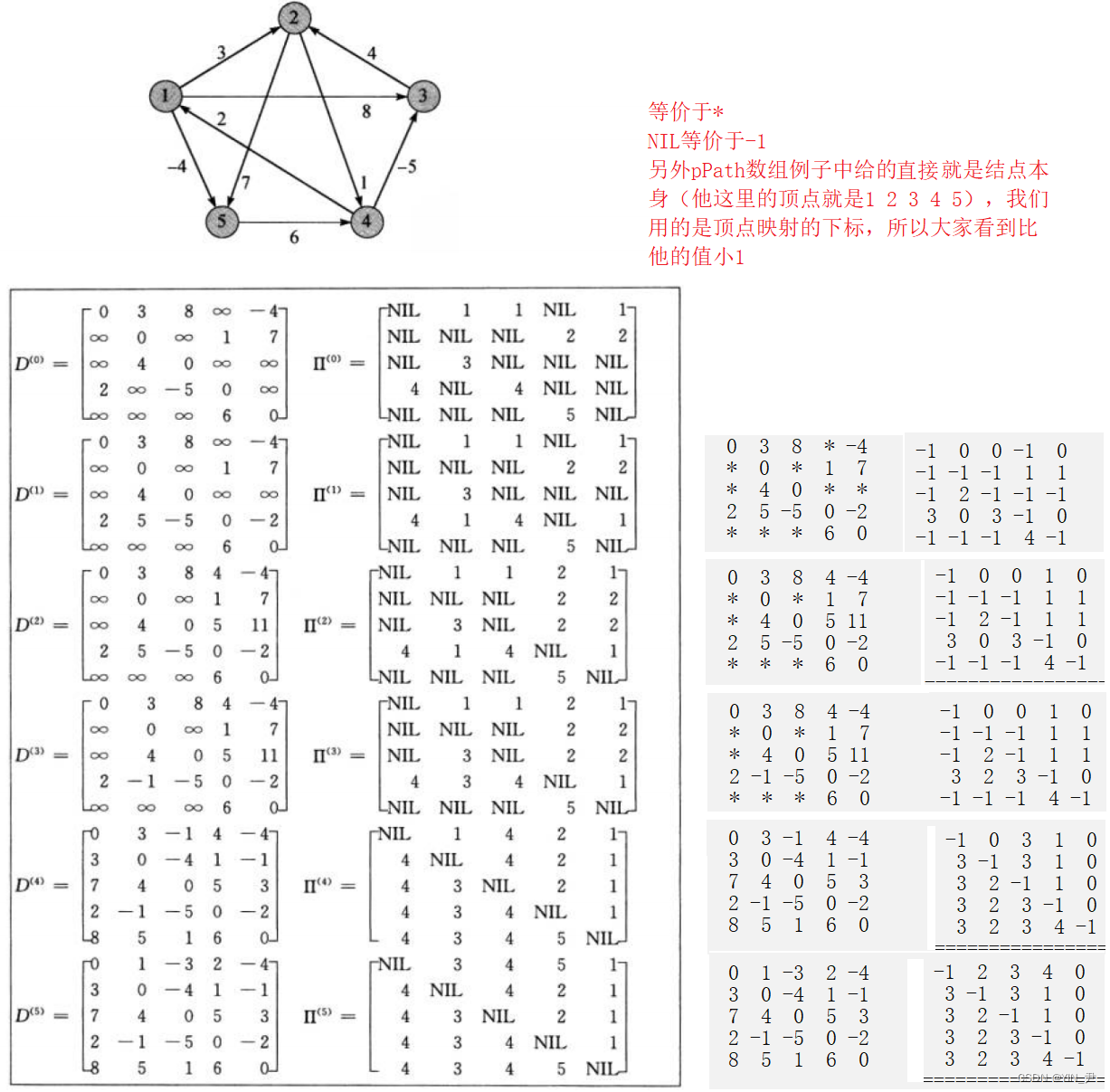
当然我们这里没有打印初始时的状态,所以我们从第二个开始对比。
那大家可以自己对照一下,应该是没问题的
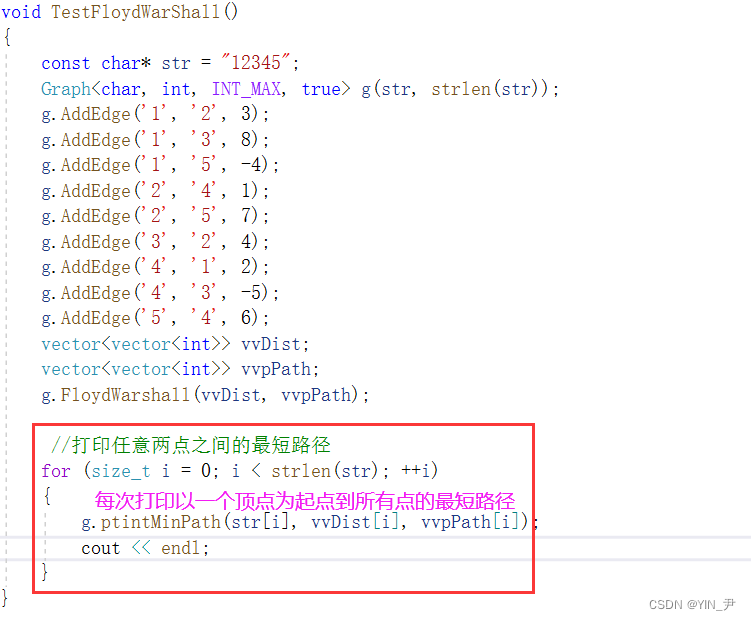
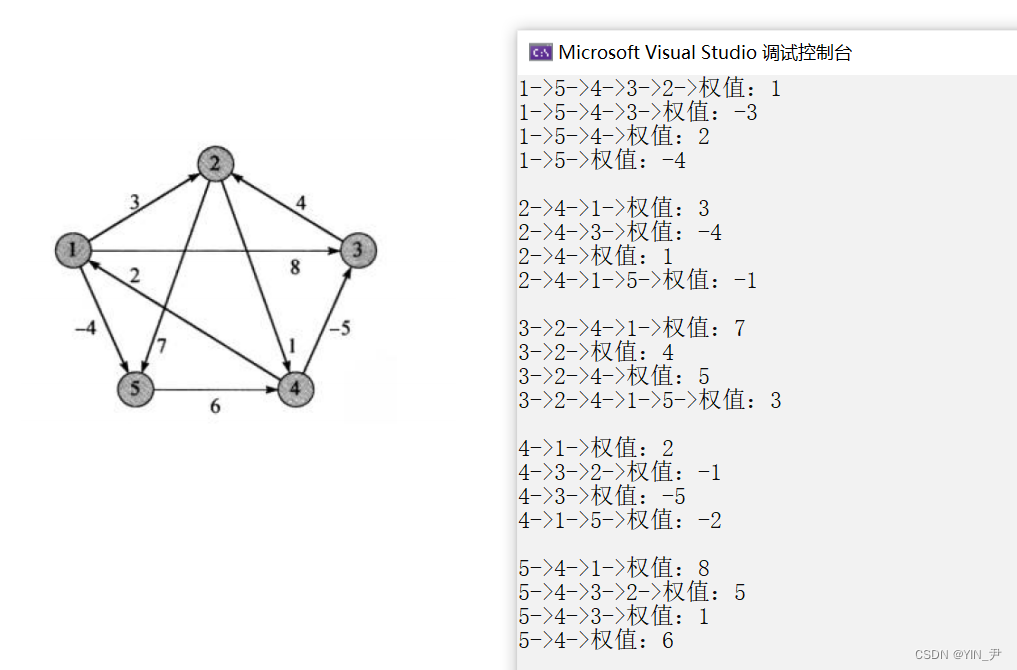
那然后呢我们可以把所有任意两点的最短路径打印一下:
任意两点的最短路径都有。
对照一下
大家可以自己对照看一下,应该没什么问题。
5. 源码
void FloydWarshall(vector<vector<W>>& vvDist, vector<vector<int>>& vvpPath)
{// 初始化一下记录路径和权值(距离)的数组size_t n = _vertexs.size();vvDist.resize(n);vvpPath.resize(n);for (size_t i = 0; i < n; ++i){vvDist[i].resize(n, MAX_W);vvpPath[i].resize(n, -1);}//把图中所有相连的边的信息先更新一下(初始状态)for (size_t i = 0; i < n; i++){for (size_t j = 0; j < n; j++){if (i == j){vvDist[i][j] = W();}if (_matrix[i][j] != MAX_W){vvDist[i][j] = _matrix[i][j];vvpPath[i][j] = i;}}}//按照状态转移方程更新ij的最短路径//依次遍历取图中的每个结点作为ij的中间结点去更新ij的最短路径for (size_t k = 0; k < n; k++){//k作为中间结点更新ij最短路径for (size_t i = 0; i < n; i++){for (size_t j = 0; j < n; j++){if (vvDist[i][k] != MAX_W&& vvDist[k][j] != MAX_W&& vvDist[i][k] + vvDist[k][j] < vvDist[i][j]){vvDist[i][j] = vvDist[i][k] + vvDist[k][j];vvpPath[i][j] = vvpPath[k][j];}}}// 打印权值和路径矩阵观察数据// for (size_t i = 0; i < n; ++i)// {// for (size_t j = 0; j < n; ++j)// {// if (vvDist[i][j] == MAX_W)// {// //cout << "*" << " ";// printf("%3c", '*');// }// else// {// //cout << vvDist[i][j] << " ";// printf("%3d", vvDist[i][j]);// }// }// cout << endl;// }// cout << endl;// for (size_t i = 0; i < n; ++i)// {// for (size_t j = 0; j < n; ++j)// {// //cout << vvParentPath[i][j] << " ";// printf("%3d", vvpPath[i][j]);// }// cout << endl;// }// cout << "=================================" << endl;}
}
void TestFloydWarShall()
{const char* str = "12345";Graph<char, int, INT_MAX, true> g(str, strlen(str));g.AddEdge('1', '2', 3);g.AddEdge('1', '3', 8);g.AddEdge('1', '5', -4);g.AddEdge('2', '4', 1);g.AddEdge('2', '5', 7);g.AddEdge('3', '2', 4);g.AddEdge('4', '1', 2);g.AddEdge('4', '3', -5);g.AddEdge('5', '4', 6);vector<vector<int>> vvDist;vector<vector<int>> vvpPath;g.FloydWarshall(vvDist, vvpPath);//打印任意两点之间的最短路径for (size_t i = 0; i < strlen(str); ++i){g.ptintMinPath(str[i], vvDist[i], vvpPath[i]);cout << endl;}
}



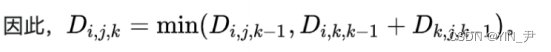







![[ROS2系列] ORBBEC(奥比中光)AstraPro相机在ROS2进行rtabmap 3D建图](https://img-blog.csdnimg.cn/933f27029fa743439f5389f503e9f7a1.png)