目录
题目:方格取数
思路:
题目:传纸条
思路:
题目:方格取数
(跑两次)

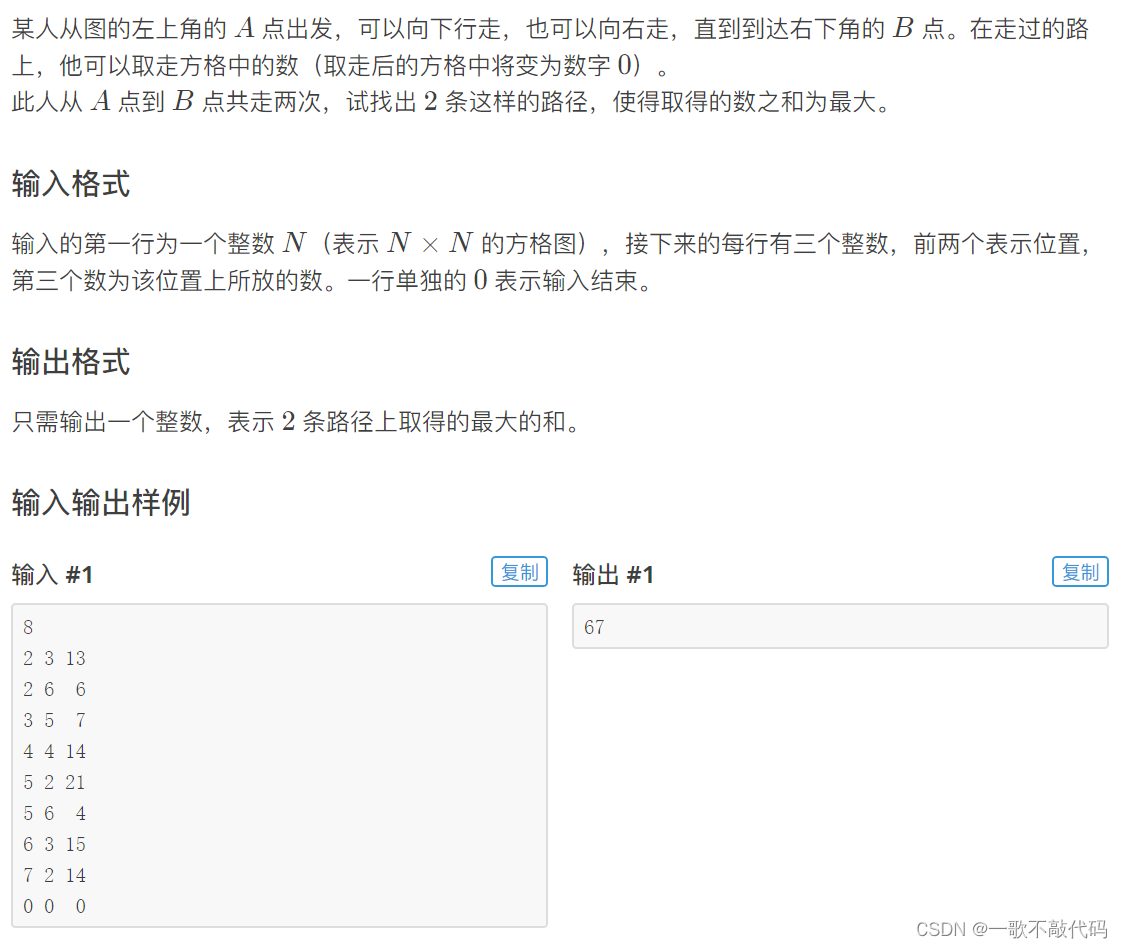
思路:
如果记录一种方案后再去跑另一个方案,影响因素太多了,所以两个方案要同时开跑。
我们设置 f[x][y][x2][y2]当第一种方案走到x,y ,第二种方案走到x2,y2时取得的最大数。
要注意不要重复取数,也即是两种方案同时走到了同一个格子,这种情况要去重。
然后就是递归方程:
if (x<N&&x2<N) M=max(M,dfs(x+1,y,x2+1,y2)+s[x+1][y]+s[x2+1][y2]-s[x+1][y]*(x+1==x2+1&&y==y2));//都向下走,如果有重复,减去重复
if (x<N&&y2<N) M=max(M,dfs(x+1,y,x2,y2+1)+s[x+1][y]+s[x2][y2+1]-s[x+1][y]*(x+1==x2&&y==y2+1));//方案1向下,2向右
if (y<N&&x2<N) M=max(M,dfs(x,y+1,x2+1,y2)+s[x][y+1]+s[x2+1][y2]-s[x][y+1]*(x==x2+1&&y+1==y2));//方案1向右,2向下
if (y<N&&y2<N) M=max(M,dfs(x,y+1,x2,y2+1)+s[x][y+1]+s[x2][y2+1]-s[x][y+1]*(x==x2&&y+1==y2+1));//都向右走也就是dfs(x,y,x2,y2)可以向下下,下右,右下,右右四种情况递归。
#include<iostream>
using namespace std; //流水的动归,铁打的递推
int N=0;
int s[15][15],f[11][11][11][11];
int dfs(int x,int y,int x2,int y2)
{if (f[x][y][x2][y2]!=-1) return f[x][y][x2][y2];//记忆化if (x==N&&y==N&&x2==N&&y2==N) return 0;//如果两种方案都走到了终点,返回结束 int M=0;if (x<N&&x2<N) M=max(M,dfs(x+1,y,x2+1,y2)+s[x+1][y]+s[x2+1][y2]-s[x+1][y]*(x+1==x2+1&&y==y2));//都向下走,如果有重复,减去重复if (x<N&&y2<N) M=max(M,dfs(x+1,y,x2,y2+1)+s[x+1][y]+s[x2][y2+1]-s[x+1][y]*(x+1==x2&&y==y2+1));//方案1向下,2向右if (y<N&&x2<N) M=max(M,dfs(x,y+1,x2+1,y2)+s[x][y+1]+s[x2+1][y2]-s[x][y+1]*(x==x2+1&&y+1==y2));//方案1向右,2向下if (y<N&&y2<N) M=max(M,dfs(x,y+1,x2,y2+1)+s[x][y+1]+s[x2][y2+1]-s[x][y+1]*(x==x2&&y+1==y2+1));//都向右走f[x][y][x2][y2]=M;//记录这种情况 return M;//返回最大值
}
int main()
{int x,y,t;cin>>N;for(int a=0;a<=N;a++)//不能memset了,必须初始化成-1,否则dfs会死循环for(int b=0;b<=N;b++)for(int c=0;c<=N;c++)for(int d=0;d<=N;d++) f[a][b][c][d]=-1;while(cin>>x>>y>>t&&(x+y+t))s[x][y]=t;cout<<dfs(1,1,1,1)+s[1][1];//输出,因为dfs中没有考虑第一格,即s[1][1],所以最后要加一下 return 0;
}
题目:传纸条

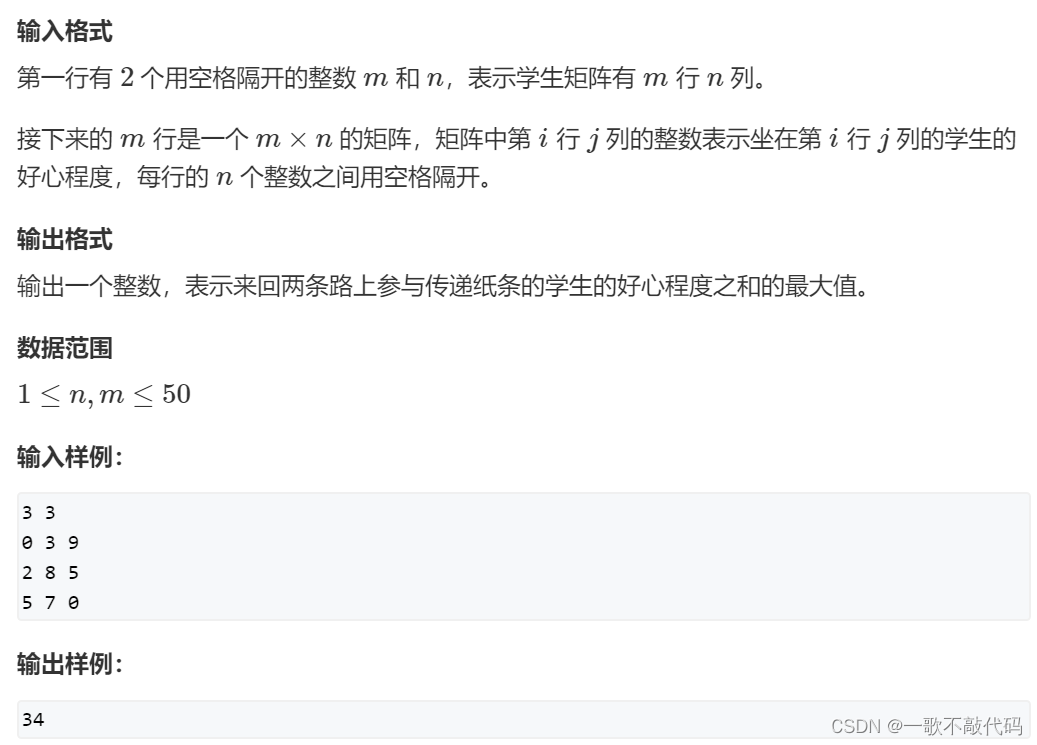
思路:
一样的思路,要同时开始跑才行。
f[x1][y1][x2][y2]表示走到两个方案分别走到(x1,y1)(x2,y2)的最优解,因为两个方案走的哈曼顿距离是一样的,可以优化成f[k][x1][x2]表示走到(x1,k-x1)(x2,k-x2)的最优解。
转移方程:f(k,x1,x2)=max{f(k-1,x1,x2),f(k-1,x1,x2-1),f(k-1,x1-1,x2),f(k-1,x1-1,x2-1)},分别为来自左左,左上,上左,上上,然后减去重复即可。
注意:1,两个人不能走同一个格子,所以x1!=x2
2,1<=k-x1<=m;故 x1<=k-1且x1>=k-m 同理x2<=k-1且x2>=k-m
#include<bits/stdc++.h>
using namespace std;
const int N = 55;
int n, m;
int g[N][N];
int f[N*2][N][N];
int main()
{scanf("%d%d", &n, &m);for (int i=1; i<=n; i++)for (int j=1; j<=m; j++){scanf("%d", &g[i][j]);}for (int k=2; k<=n+m; k++)for (int x1=max(1,k-m); x1<=min(k-1,n); x1++)for (int x2=max(1,k-m); x2<=min(k-1,n); x2++){int t=g[x1][k-x1];//当前好心度if(x2!=x1) t+=g[x2][k-x2];for (int a=0; a<=1; a++)for (int b=0; b<=1; b++){f[k][x1][x2]=max(f[k][x1][x2],f[k-1][x1-a][x2-b]+t);}}printf("%d\n", f[n+m][n][n]);return 0;
}