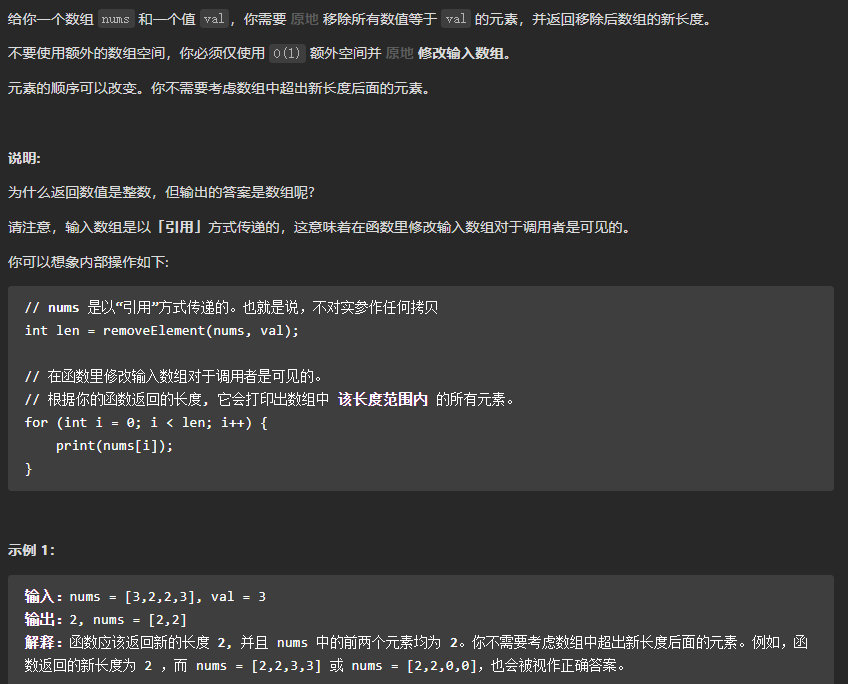
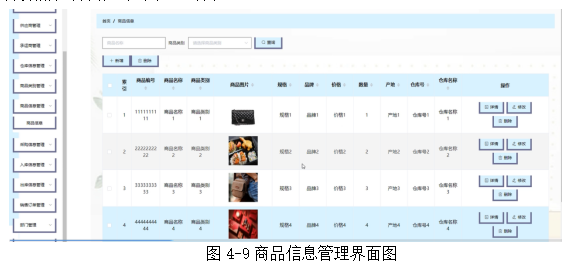
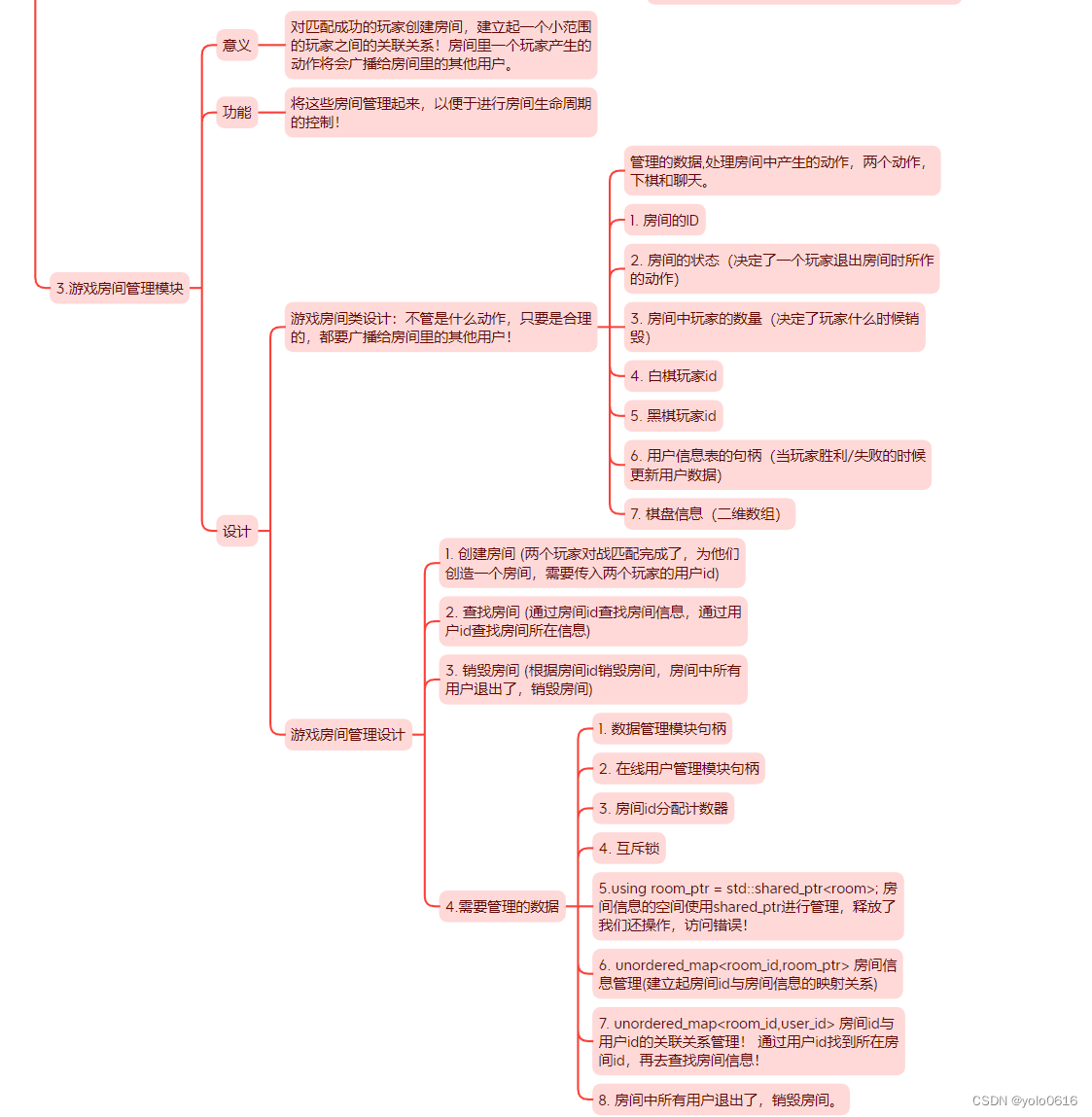
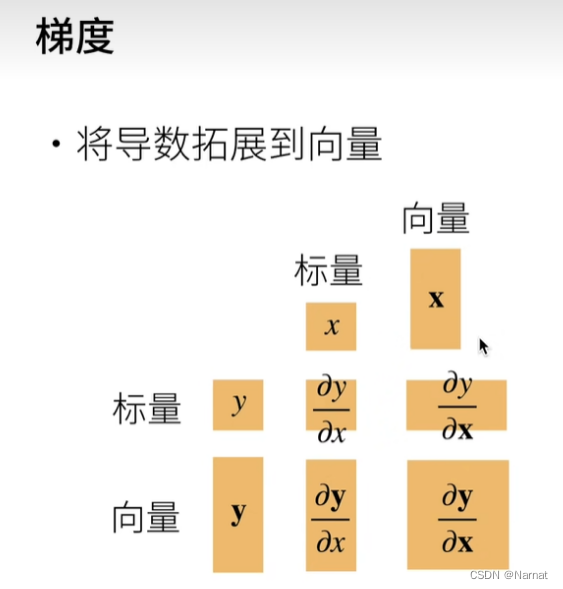
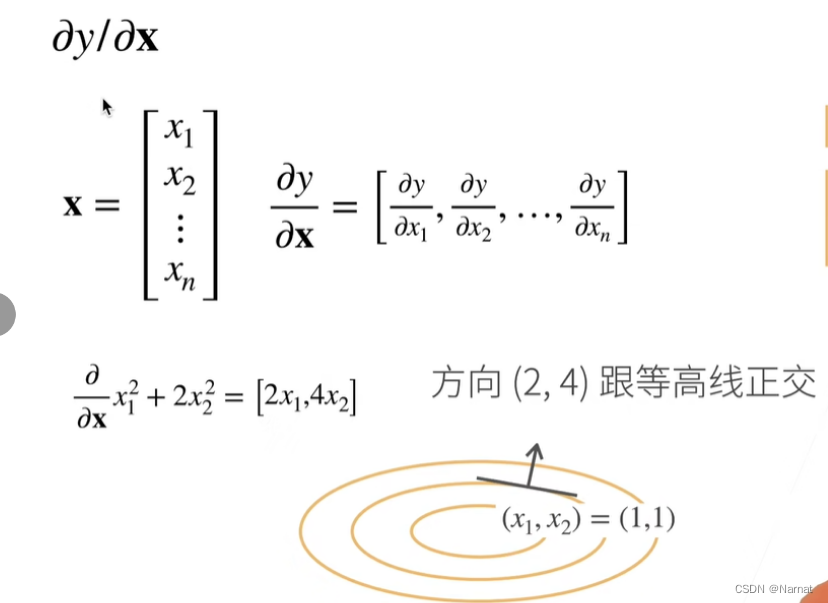
梯度

实战




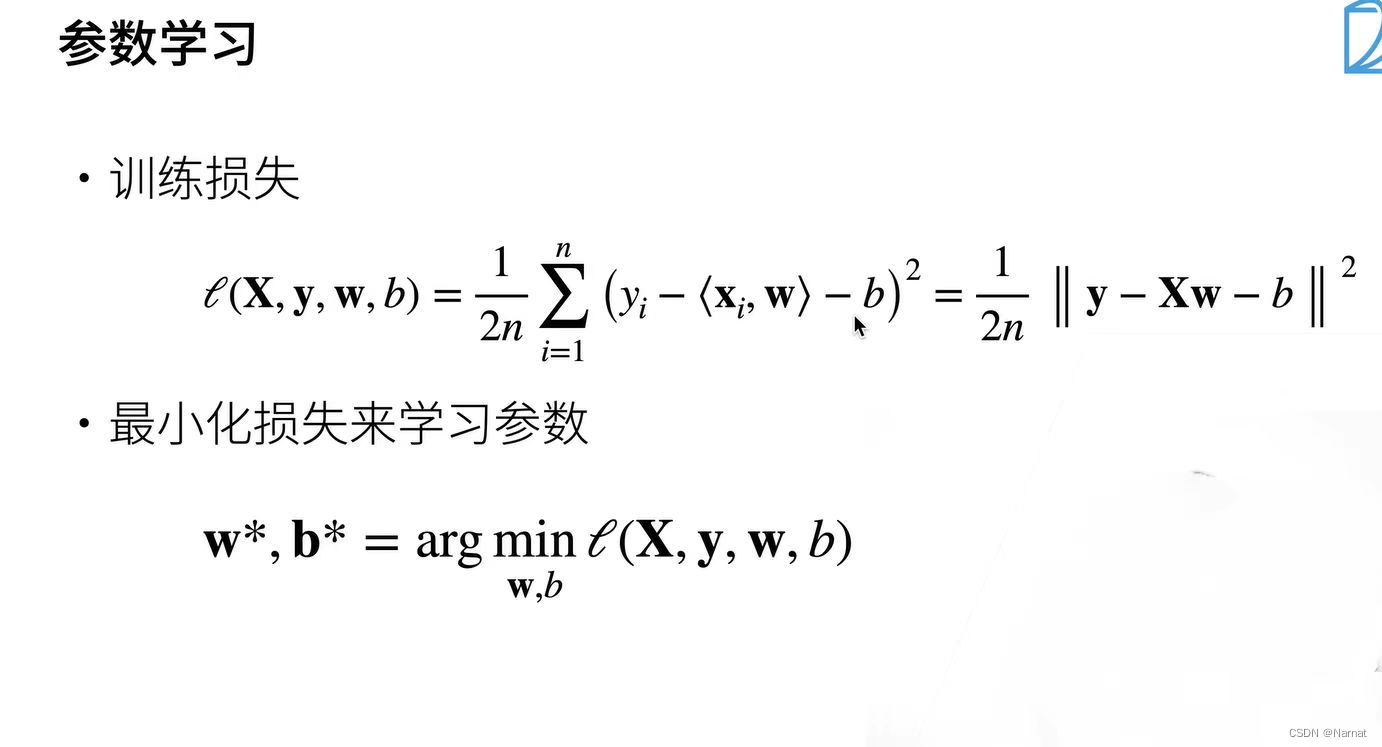

代码:
# %matplotlib inline
import random
import torch
import matplotlib.pyplot as plt
# from d21 import torch as d21def synthetic_data(w, b, num_examples):"""生成 Y = XW + b + 噪声。"""X = torch.normal(0, 1, (num_examples, len(w)))# 均值为0,方差为1的随机数,n个样本,列数为w的长度y = torch.matmul(X, w) + b # y = x * w + by += torch.normal(0, 0.01, y.shape) # 加入随机噪音,均值为0.。形状与y的一样return X, y.reshape((-1, 1))# x, y做成列向量返回true_w = torch.tensor([2, -3.4])
true_b = 4.2
features, labels = synthetic_data(true_w, true_b, 1000)
#读取小批量,输出batch_size的小批量,随机选取
def data_iter(batch_size, features, labels):num_examples = len(features)indices = list(range(num_examples))#转成listrandom.shuffle(indices)#打乱for i in range(0, num_examples, batch_size):#batch_indices = torch.tensor(indices[i:min(i + batch_size, num_examples)])#取yield features[batch_indices], labels[batch_indices]#不断返回# #print(features)
# #print(labels)
#
#
batch_size = 10
#
# for x, y in data_iter(batch_size, features,labels):
# print(x, '\n', y)
# break
# # 提取第一列特征作为x轴,第二列特征作为y轴
# x = features[:, 1].detach().numpy() #将特征和标签转换为NumPy数组,以便能够在Matplotlib中使用。
# y = labels.detach().numpy()
#
# # 绘制散点图
# plt.scatter(x, y, 1)
# plt.xlabel('Feature 1')
# plt.ylabel('Feature 2')
# plt.title('Synthetic Data')
# plt.show()
#
# #定义初始化模型w = torch.normal(0, 0.01, size=(2, 1), requires_grad=True)
b = torch.zeros(1, requires_grad = True)def linreg(x, w, b):return torch.matmul(x, w) + b#定义损失函数def squared_loss(y_hat, y):return (y_hat - y.reshape(y_hat.shape))**2 / 2 #弄成一样的形状# 定义优化算法
def sgd(params, lr, batch_size):"""小批量随梯度下降"""with torch.no_grad():#节省内存和计算资源。for param in params:param -= lr * param.grad / batch_sizeparam.grad.zero_()#用于清空张量param的梯度信息。print("训练函数")lr = 0.03 #学习率
num_ecopchs = 300 #数据扫描三遍
net = linreg #指定模型
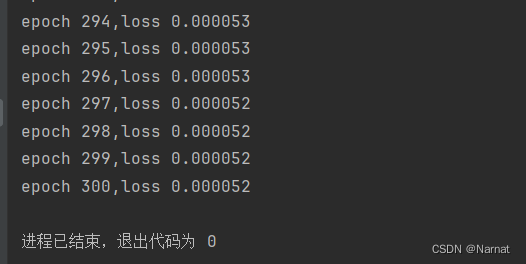
loss = squared_loss #损失for epoch in range(num_ecopchs):#扫描数据for x, y in data_iter(batch_size, features, labels): #拿出x, yl = loss(net(x, w, b), y)#求损失,预测net,真实yl.sum().backward()#算梯度sgd([w, b], lr, batch_size)#使用参数的梯度更新参数with torch.no_grad():train_l = loss(net(features, w, b), labels)print(f'epoch {epoch + 1},loss {float(train_l.mean()):f}')运行效果: