零、前言 :
最近在学习自动驾驶方向的东西,简单整理一些学习笔记,学习过程中发现宝藏up 手写AI
一、视觉系统坐标系
视觉系统一共有四个坐标系:像素平面坐标系(u,v)、图像坐标系(x,y)、相机坐标系 ( x c , y c , z c ) (x_c , y_c , z_c ) (xc,yc,zc)和世界坐标系 ( x ω , y ω , z ω ) (x_ω,y_ω,z_ω) (xω,yω,zω),每种坐标系之间均存在练习。通过图像像素坐标定位到世界坐标系的坐标,需要通过相机标定来解决,其中关键的算法部分在于坐标系转换,而变换需要通过齐次坐标的表示方式来完成。
二、各个坐标系介绍
1. 相机坐标系系统
摄像头的作用是把三维世界中的形状、颜色信息,压缩到一张二维图像上。基于摄像头的感知算法则是从二维图像中提取并还原三维世界中的元素和信息,如车道线、车辆、行人等,并且计算他们与车辆的相对位置;感知算法和相机相关的坐标系有图像坐标系(像素坐标系)、摄像机坐标系、像屏幕坐标系。
1.1 像素坐标系(图像坐标系)
电脑上存储的图像一般以左上角为原点,向右为x正方向,向下为y正方向,单位以’像素’最为常用。图像坐标系为二维坐标系,记为 ( X i , Y i ) (X_i, Y_i) (Xi,Yi)
1.2 摄像机坐标系
由于图像坐标系向右为x,向下为y,所以摄像机坐标系以镜头主光轴中心为原点,一般向右为x正方向,向下为y正方向,向前为z正方向,x, y方向与图像坐标系方向吻合,z方向即为景深,摄像机坐标系记为 ( X c , Y c ) (X_c, Y_c) (Xc,Yc)
1.3 像平面坐标系(成像坐标系)
为了能够定量描述三维空间到二维图像的映射关系,图形学里引入了像平面坐标系,是摄像机坐标系的一个平移,中心仍在摄像机主光轴上。距离光轴中心的距离等于摄像机的焦距,摄像机会在光轴中心后方的底片上成一个缩小的倒像,是真正的像平面 ( X f ′ , Y f ′ ) (X'_f, Y'_f) (Xf′,Yf′),但是为了分析和计算方便,我们会在光轴中心前方设立一个虚拟像平面上的成像 ( X f , Y f ) (X_f, Y_f) (Xf,Yf)为正像,大小与真实倒像相同。
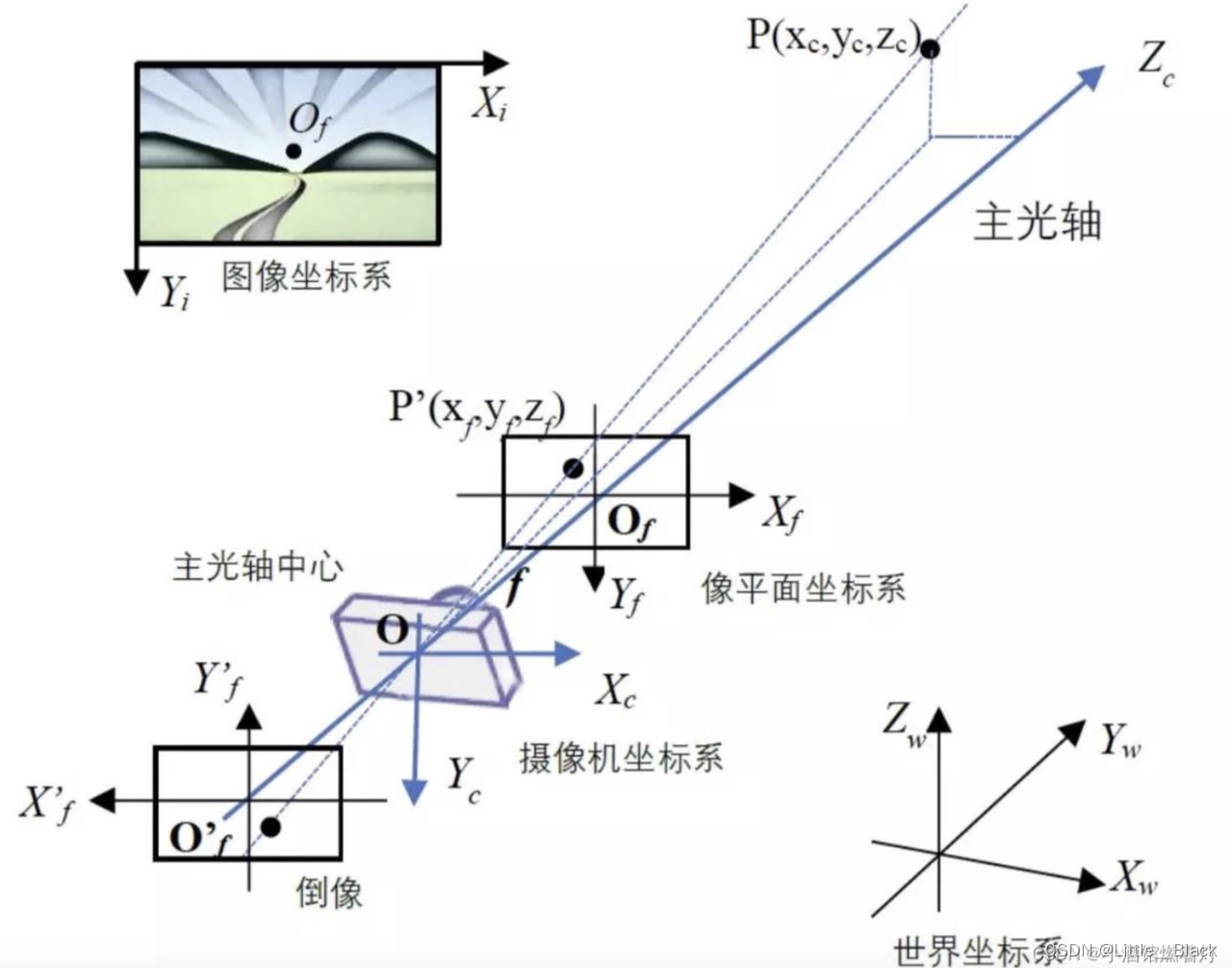
1.4 世界坐标系:可以表示任何物体,此时是由相机引入的,单位是m,各个坐标系的关系如下:
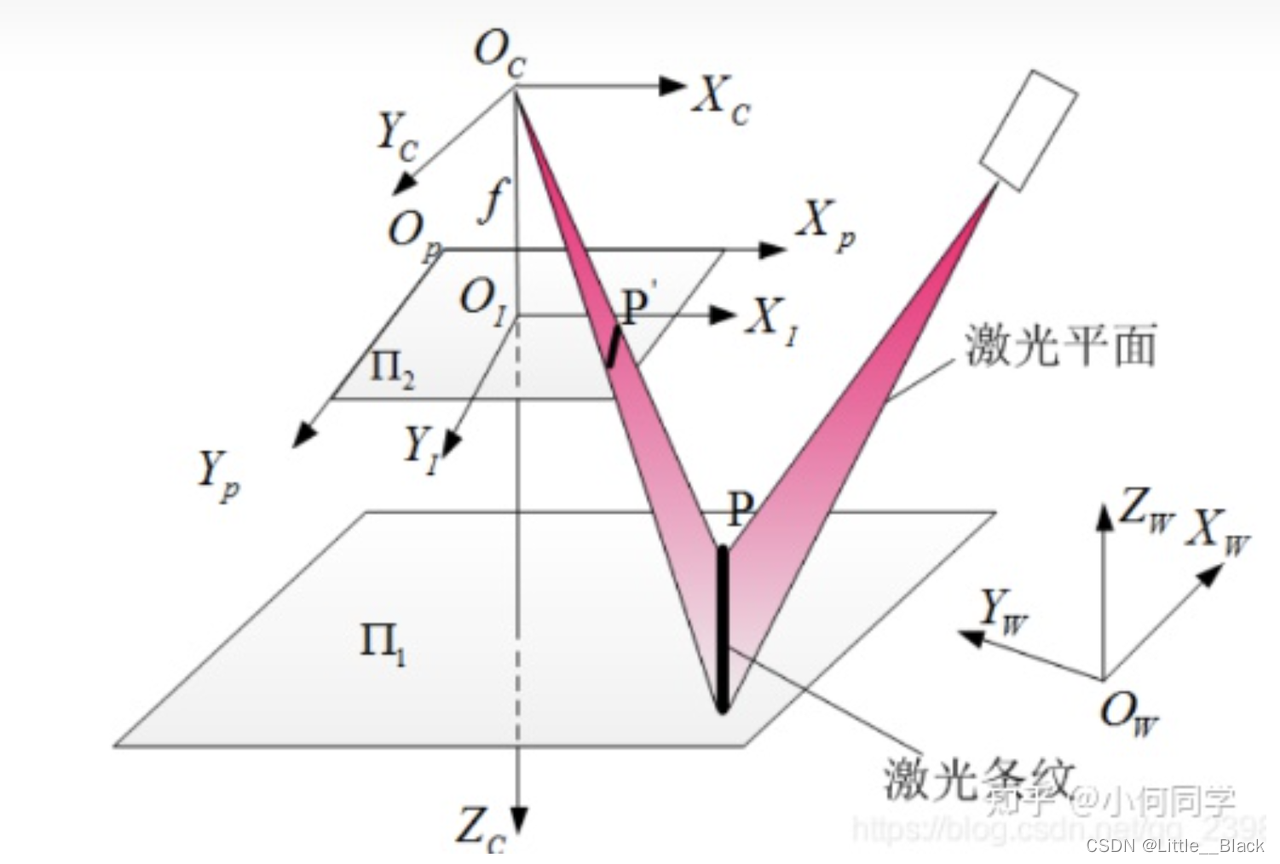
其中 世界坐标系 O w X w Y w Z w O_wX_wY_wZ_w OwXwYwZw 、相机坐标系 O c X c Y c Z c O_cX_cY_cZ_c OcXcYcZc、成像坐标系 O I X I Y I Z I O_IX_IY_IZ_I OIXIYIZI 及像素坐标系 O p X p Y p Z p O_pX_pY_pZ_p OpXpYpZp
2. Lidar 坐标系
Lidar常被用作一个主要的传感器来获取周围环境的3D信息。在多数情况下,Lidar坐标系为右手坐标系,但具体定义可能会因Lidar制造商而异。
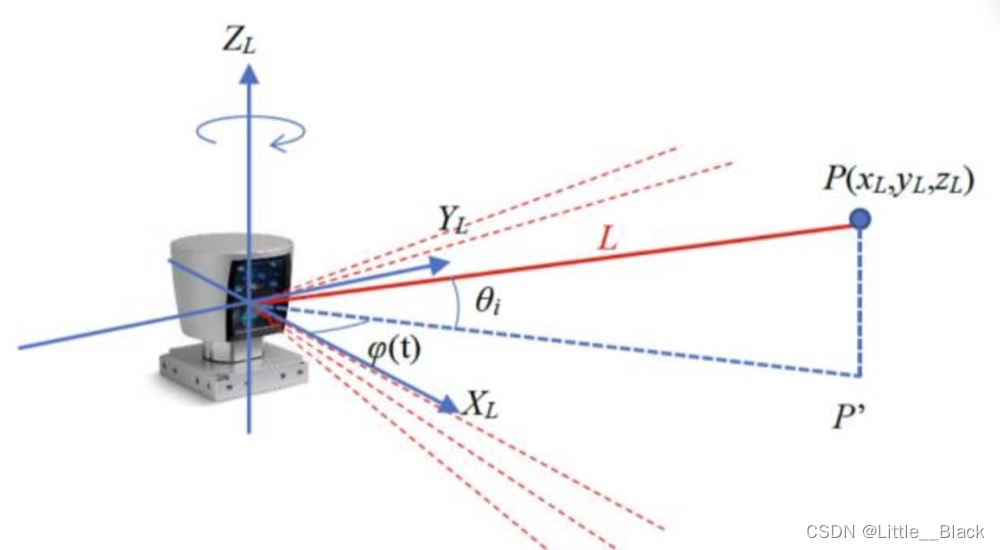
2.1 雷达参数的定义
- X轴:通常指向Lidar前方,当激光束指向前发射时,与该放下的距离测量会在x轴上产生一个正值
- Y轴:通常指向Lidar左侧,当激光束指向左侧发射时,与该放下的距离测量会在y轴上产生一个正值
- Z轴:通常指向Lidar上方,与X和Y垂直,高度测量通常沿Z轴进行,正值代表物体高于Lidar设备,负值代表低于Lidar设备。
车载Lidar系统的坐标系与车辆坐标系可能不完全对齐,需要一个转换矩阵来在两者之间进行坐标变换,当与摄像头、雷达或其他传感器进行数据融合时,通常需要知道Lidar与这些传感器之间的外部标定参数(如 旋转和平移矩阵),以便在他们之间进行坐标变换。
- 自车坐标系
一般环境中选择一个参考坐标系来描述传感器和物体的位置,该坐标系称为世界坐标系;紫车坐标系指的是以车体后轴中心为原点(因为后轴中心不会随着车摆动而发生相对变化),左前上或右前上的空间坐标系,左(右)一般为横向,前一般为纵向,上指地面以上空间,坐标随车运动而运动,所有的下游需要感知输出的目标都要在自车坐标系下面,BEV视角目标也是指的在这个坐标下。
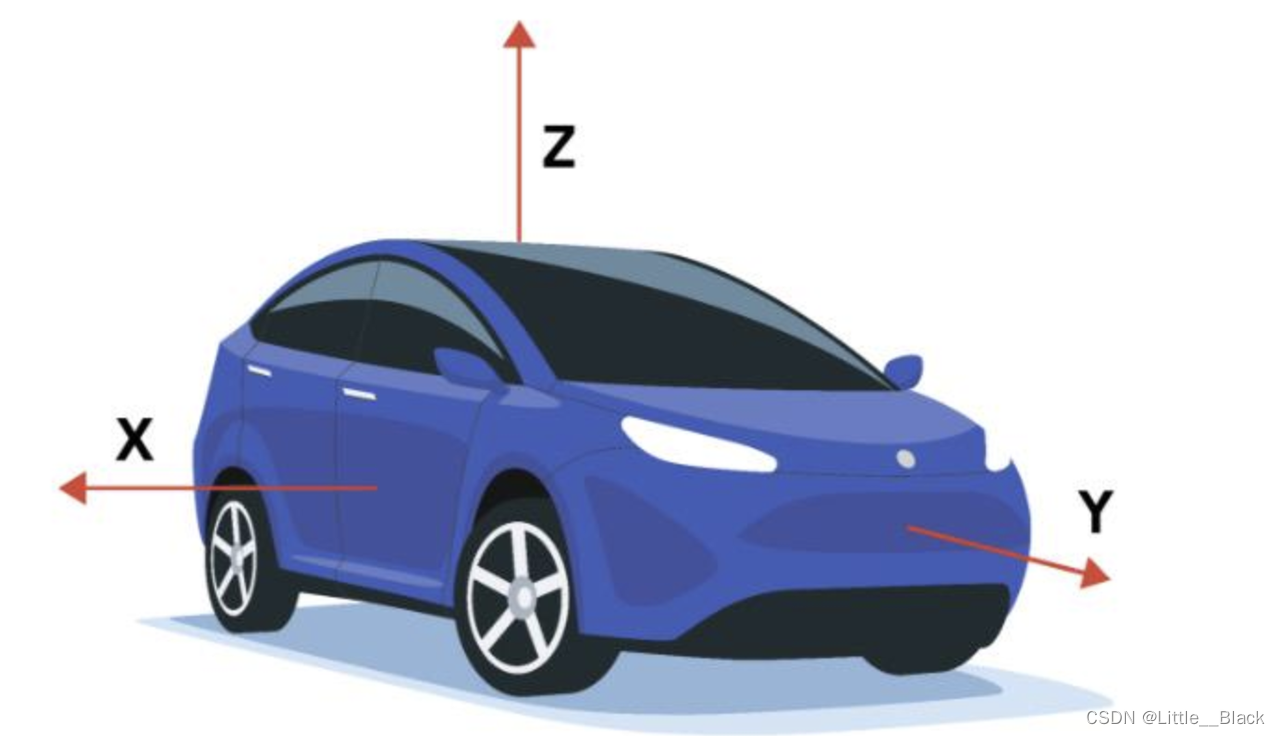
一般三维空间坐标系用三个正交轴X,Y,Z表示物体的位置,用绕这三个正交轴的旋转角度(roll 滚动角, pitch 俯仰角, yaw 偏航角)表示物体的姿态。时间坐标系只有一个维度。 - 相机的参数
- 相机内参: 内参用来确定摄像机从三维空间到二维图像的投影关系,主要包含三个参数(相机主点、相机焦距、畸变系数),内参是由商家提供,自驾领域。摄像机的内参为常数,使用中不会发生变化,但需要再使用前做好标定工作,摄像机的拍摄过程可以抽象为是从三维摄像机坐标系映射到二维像平面坐标系,再映射到图像坐标系的过程。
- 焦距(f): 描述了图像传感器与摄像机的透镜之间的距离。通常用两个参数 ( f x ) (f_x) (fx)和 ( f y ) (f_y) (fy)来表示,分别对应于图像的x轴和y轴,很多情况下,假定 ( f x = f y ) (f_x=f_y) (fx=fy),这意味着像素在两个方向上都是正方向的
- 主点:是图像中的一个点,通常接近图像的中心,它是3D空间中的点投影到图像平面时所对应的2D点,通常用两个参数 ( c x , c y ) (c_x, c_y) (cx,cy)表示,对应于图像的x轴和y轴上的坐标
- 畸变系数:真实的透镜可能会引入畸变,导致图像失真,场景的畸变有径向畸变和切向畸变,常见的径向畸变系数为 ( k 1 , k 2 , k 3 ) (k_1,k_2, k_3) (k1,k2,k3), 切向畸变系数为 ( p 1 , p 2 ) (p_1, p_2) (p1,p2)。
- 摄像机的内参可以表示为一个矩阵:
$ K = [ f x 0 c x 0 f y c y 0 0 1 ] K=\left[ \begin{matrix} f_x & 0 & c_x \\ 0 &f_y & c_y \\ 0 & 0 & 1\\ \end{matrix} \right] K= fx000fy0cxcy1
这个矩阵通常被称为内参矩阵或者相机矩阵 - 相机外参:通过二维图像推断物体在三维摄像机坐标系中的位置,例如获得距离深度信息。从二维图像中获取三维距离信息,如果需要获取物体在世界坐标系中的位置,则还需要知道摄像机在世界坐标系中的位姿;这一位姿表示被称为摄像机的外部参数,简称外参,用来决定摄像机坐标与世界坐标之间相对位置关系,在自驾领域,得到这一位置关系还需要一系列的标定和定位工作;相机相对于其他坐标系,旋转+平移矩阵,其中旋转外参与上述欧拉角[yaw, patch,roll],旋转顺序一般为(z-y-x),单位为度,平移外参,相机到目标坐标系中的平移距离,单位米。
三、坐标系之间的关系
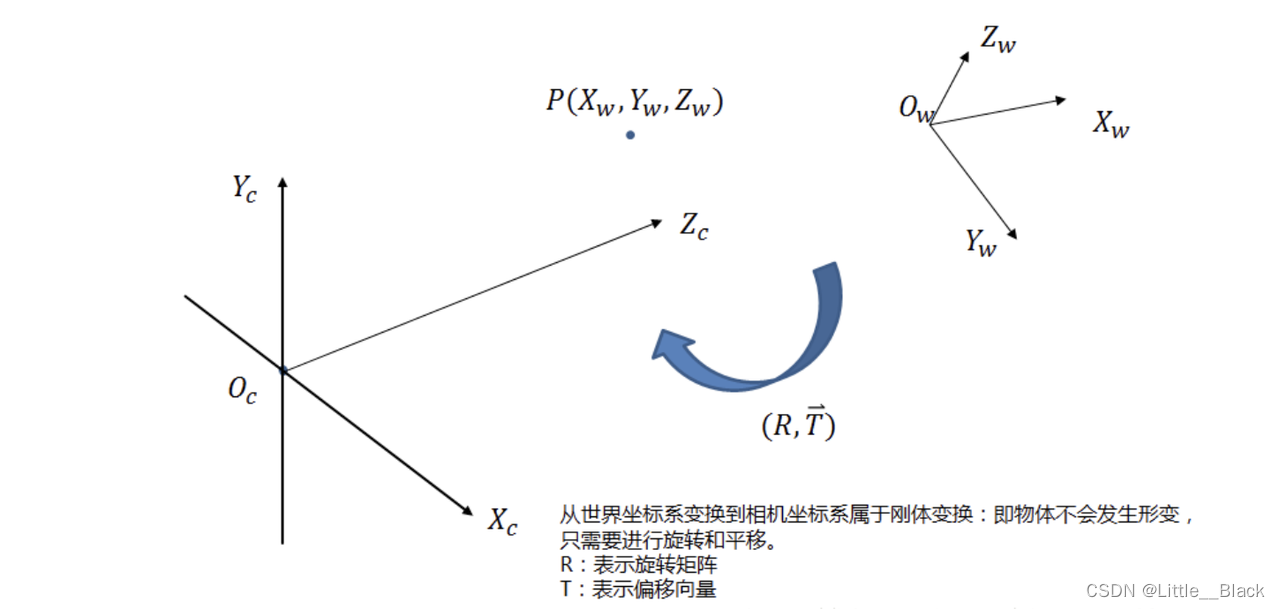
- 世界坐标系到相机坐标系
物体之间的坐标系变换都可以表示坐标系的旋转变换加上平移变换,则世界坐标系到相机坐标系的转换关系也是如此。绕着不同的轴旋转不同的角度得到不同的旋转矩阵。如图,绕z轴旋转的示意图:
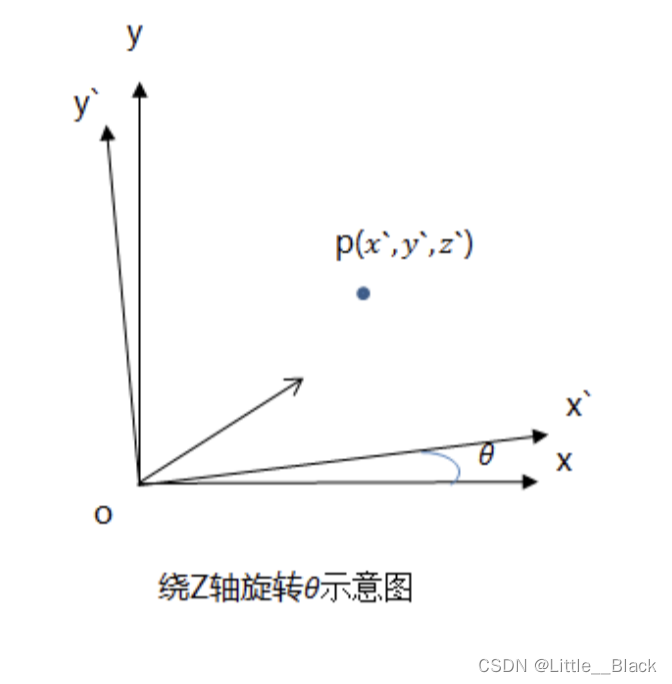
由图可得:
{ x = x ′ c o s θ − y ′ s i n θ y = x ′ s i n θ + y ′ c o s θ z = z ′ \begin{cases}x=x^′cosθ−y^′sinθ \\ y=x^′sinθ+y^′cosθ \\ z=z^′ \end{cases} ⎩ ⎨ ⎧x=x′cosθ−y′sinθy=x′sinθ+y′cosθz=z′ 转换成矩阵形式就是: [ x y z ] = [ c o s θ − s i n θ 0 s i n θ c o s θ 0 0 0 1 ] [ x ′ y ′ z ′ ] = R 1 [ x ′ y ′ z ′ ] \left[ \begin{matrix} x \\ y \\ z \\ \end{matrix} \right] = \left[ \begin{matrix} cosθ&-sinθ&0\\ sinθ&cosθ&0 \\ 0&0&1 \\ \end{matrix} \right] \left[ \begin{matrix} x^′ \\ y^′ \\ z^′ \\ \end{matrix} \right] = R_1\left[ \begin{matrix} x^′ \\ y^′ \\ z^′ \\ \end{matrix} \right] xyz = cosθsinθ0−sinθcosθ0001 x′y′z′ =R1 x′y′z′
同理,绕x,y轴旋转可得:
[ x y z ] = [ 1 0 0 0 c o s ϕ s i n ϕ 0 − s i n ϕ c o s ϕ ] [ x ′ y ′ z ′ ] = R 2 [ x ′ y ′ z ′ ] \left[ \begin{matrix} x \\ y \\ z \\ \end{matrix} \right] = \left[ \begin{matrix} 1&0&0\\ 0&cosϕ&sinϕ \\ 0&-sinϕ&cosϕ \\ \end{matrix} \right] \left[ \begin{matrix} x^′ \\ y^′ \\ z^′ \\ \end{matrix} \right] = R_2\left[ \begin{matrix} x^′ \\ y^′ \\ z^′ \\ \end{matrix} \right] xyz = 1000cosϕ−sinϕ0sinϕcosϕ x′y′z′ =R2 x′y′z′
[ x y z ] = [ c o s w 0 − s i n w 0 1 0 s i n w 0 c o s w ] [ x ′ y ′ z ′ ] = R 3 [ x ′ y ′ z ′ ] \left[ \begin{matrix} x \\ y \\ z \\ \end{matrix} \right] = \left[ \begin{matrix} cosw&0&-sinw\\ 0&1&0 \\ sinw&0&cosw \\ \end{matrix} \right] \left[ \begin{matrix} x^′ \\ y^′ \\ z^′ \\ \end{matrix} \right] = R_3\left[ \begin{matrix} x^′ \\ y^′ \\ z^′ \\ \end{matrix} \right] xyz = cosw0sinw010−sinw0cosw x′y′z′ =R3 x′y′z′
最后可以简单总结为旋转矩阵为:
R = R 1 R 2 R 3 R = R_1R_2R_3 R=R1R2R3
平移世界坐标点 ( x w , y w , z w ) (x_w,y_w,z_w) (xw,yw,zw)距离为 ( t x , t y , t z ) (t_x,t_y,t_z) (tx,ty,tz)到相机坐标点 ( x c , y c , z c ) (x_c,y_c,z_c) (xc,yc,zc),则有:
[ x c y c z c 1 ] = [ 1 0 0 t x 0 1 0 t y 0 0 1 t z 0 0 0 1 ] [ x w y w z w 1 ] \left[ \begin{matrix} x_c \\ y_c \\ z_c \\ 1 \\ \end{matrix} \right] = \left[ \begin{matrix} 1&0&0&t_x\\ 0&1&0&t_y \\ 0&0&1&t_z \\ 0&0&0& 1 \\ \end{matrix} \right] \left[ \begin{matrix} x_w \\ y_w \\ z_w \\ 1 \ \end{matrix} \right] xcyczc1 = 100001000010txtytz1 xwywzw1
所以,世界坐标系中的点变换到相机坐标系后的坐标:
[ X c Y c Z c ] = R [ X w Y w Z w ] + T \left[ \begin{matrix} X_c \\ Y_c \\ Z_c \\ \end{matrix} \right]=R \left[ \begin{matrix} X_w \\ Y_w \\ Z_w \\ \end{matrix} \right] + T XcYcZc =R XwYwZw +T ===> [ X c Y c Z c 1 ] = [ R T 0 ⇀ 1 ] [ X w Y w Z w 1 ] \left[ \begin{matrix} X_c \\ Y_c \\ Z_c \\ 1 \\ \end{matrix} \right]=\left[ \begin{matrix}R&T\\ \overset{\rightharpoonup}{0}&1 \end{matrix} \right] \left[ \begin{matrix} X_w \\ Y_w \\ Z_w \\ 1 \\ \end{matrix} \right] XcYcZc1 =[R0⇀T1] XwYwZw1 R: 3x3, T: 3x1
2. 相机坐标系到图像物理坐标系
从相机坐标系到图像坐标系,属于透视投影关系,从3D转换到2D,也可以看成是针孔模型的改变模型,满足三角形相似定理。
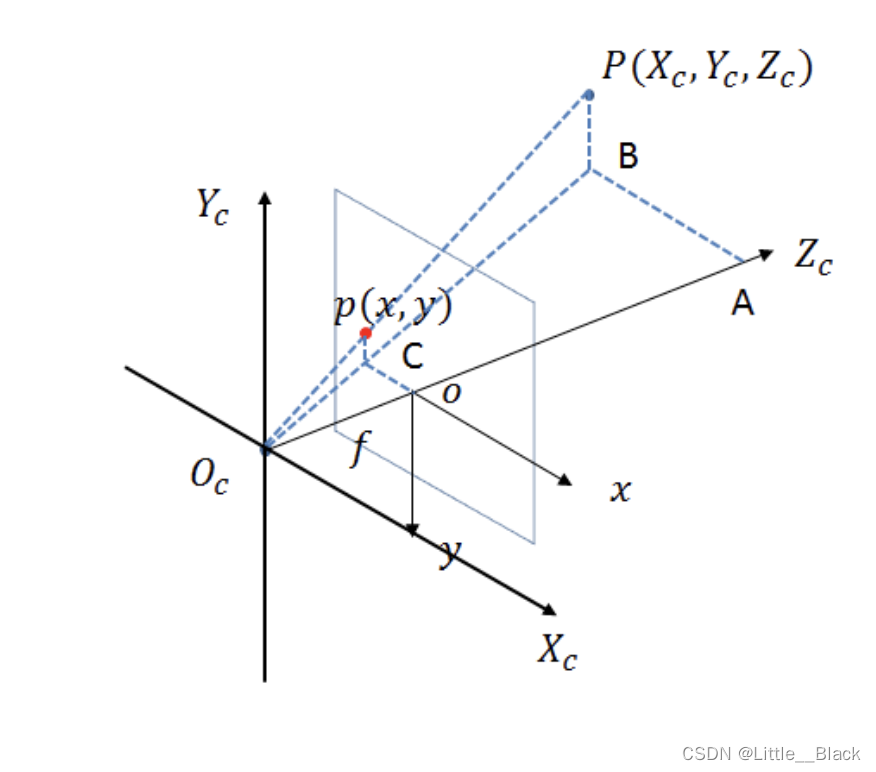
Δ A B O c \Delta ABO_c ΔABOc ~ Δ o C O c \Delta oCO_c ΔoCOc
Δ P B O c \Delta PBO_c ΔPBOc ~ Δ p C O c \Delta pCO_c ΔpCOc
则有:
A B o C = A O c o O c = P B p C = X c x = Z c f = Y c y \frac{AB}{oC} = \frac{AO_c}{oO_c}=\frac{PB}{pC} = \frac{X_c}{x} = \frac{Z_c}{f}=\frac{Y_c}{y} oCAB=oOcAOc=pCPB=xXc=fZc=yYc
则可得:
x = f X c Z c , y = f Y c Z c x=f\frac{X_c}{Z_c}, y=f\frac{Y_c}{Z_c} x=fZcXc,y=fZcYc
Z c [ x y 1 ] = [ f 0 0 0 0 f 0 0 0 0 1 0 ] [ X c Y c Z c 1 ] Z_c\left[ \begin{matrix} x \\ y \\ 1 \\ \end{matrix} \right] = \left[ \begin{matrix} f&0&0&0 \\ 0&f&0&0 \\ 0&0&1&0 \\ \end{matrix} \right]\left[ \begin{matrix} X_c \\ Y_c \\ Z_c \\ 1 \\ \end{matrix} \right] Zc xy1 = f000f0001000 XcYcZc1
3. 图像物理坐标系到像素坐标系
此时与前面的坐标系变换不同,没有旋转变换,但是坐标原点位置不一致,大小不一致,则设计伸缩变换及平移变换即可:

{ u = x d x + u 0 v = y d y + v 0 \begin{cases} u = \frac{x}{dx} + u_0 \\ v = \frac{y}{dy} + v_0 \end{cases} {u=dxx+u0v=dyy+v0
则可以得到:
[ u v 1 ] = [ 1 d x 0 u 0 0 1 d y v 0 0 0 1 ] [ x y 1 ] \left[ \begin{matrix} u \\ v \\ 1 \\ \end{matrix} \right] = \left[ \begin{matrix} \frac{1}{dx} & 0 & u_0 \\ 0 & \frac{1}{dy} & v_0 \\ 0 & 0 & 1 \\ \end{matrix} \right] \left[ \begin{matrix} x \\ y \\ 1 \\ \end{matrix} \right] uv1 = dx1000dy10u0v01 xy1
总的关系变化为(矩阵依次左乘):
像素坐标 ( u , v ) (u,v) (u,v) <–(二次转换)-- 图像坐标 ( x , y ) (x,y) (x,y) <–(透视投影)-- 图像坐标 ( X c , Y c , Z c ) (X_c, Y_c, Z_c) (Xc,Yc,Zc) <–(刚体变换)-- 图像坐标 ( X w , Y w , Z w ) (X_w, Y_w, Z_w) (Xw,Yw,Zw)
Z c [ u v 1 ] = [ 1 d x 0 u 0 0 1 d y v 0 0 0 1 ] [ f 0 0 0 0 f 0 0 0 0 1 0 ] [ R T 0 ⇀ 1 ] [ X w Y w Z w 1 ] Z_c \left[ \begin{matrix} u \\ v \\ 1 \\ \end{matrix} \right] = \left[ \begin{matrix} \frac{1}{dx} & 0 & u_0 \\ 0 & \frac{1}{dy} & v_0 \\ 0 & 0 & 1 \\ \end{matrix} \right] \left[ \begin{matrix} f&0&0&0 \\ 0&f&0&0 \\ 0&0&1&0 \\ \end{matrix} \right] \left[ \begin{matrix}R&T\\ \overset{\rightharpoonup}{0}&1 \end{matrix} \right] \left[ \begin{matrix} X_w \\ Y_w \\ Z_w \\ 1 \\ \end{matrix} \right] Zc uv1 = dx1000dy10u0v01 f000f0001000 [R0⇀T1] XwYwZw1
= [ f x 0 u 0 0 0 f y v 0 0 0 0 1 0 ] [ R T 0 ⇀ 1 ] [ X w Y w Z w 1 ] = \left[ \begin{matrix} f_x&0&u_0&0 \\ 0&f_y&v_0&0 \\ 0&0&1&0 \\ \end{matrix} \right] \left[ \begin{matrix}R&T\\ \overset{\rightharpoonup}{0}&1 \end{matrix} \right] \left[ \begin{matrix} X_w \\ Y_w \\ Z_w \\ 1 \\ \end{matrix} \right] = fx000fy0u0v01000 [R0⇀T1] XwYwZw1
其中 [ R T 0 ⇀ 1 ] \left[ \begin{matrix}R&T\\ \overset{\rightharpoonup}{0}&1 \end{matrix} \right] [R0⇀T1]为相机外参,R和T分别为旋转和平移量 [ f x 0 u 0 0 0 f y v 0 0 0 0 1 0 ] \left[ \begin{matrix} f_x&0&u_0&0 \\ 0&f_y&v_0&0 \\ 0&0&1&0 \\ \end{matrix} \right] fx000fy0u0v01000 为相机内参,内参是固有属性,实际上就是焦距f,像元尺寸dx, dy ,很明显 Z c Z_c Zc 表示的是点离光轴的距离。
同样的有:
[ X w Y w Z w 1 ] = [ R T 0 ⇀ 1 ] [ Z c f 0 0 0 Z c f 0 0 0 Z c 0 0 1 ] [ d x 0 − u 0 d x 0 d y − v 0 d y 0 0 1 ] [ u v 1 ] \left[ \begin{matrix} X_w \\ Y_w \\ Z_w \\ 1 \\ \end{matrix} \right] =\left[ \begin{matrix}R&T\\ \overset{\rightharpoonup}{0}&1 \end{matrix} \right] \left[ \begin{matrix} \frac{Z_c}{f}&0&0 \\ 0&\frac{Z_c}{f}&0 \\ 0&0&Z_c \\ 0&0&1 \\ \end{matrix} \right] \left[ \begin{matrix} dx & 0 & -u_0dx \\ 0 & dy & -v_0dy \\ 0 & 0 & 1 \\ \end{matrix} \right] \left[ \begin{matrix} u \\ v \\ 1 \\ \end{matrix} \right] XwYwZw1 =[R0⇀T1] fZc0000fZc0000Zc1 dx000dy0−u0dx−v0dy1 uv1