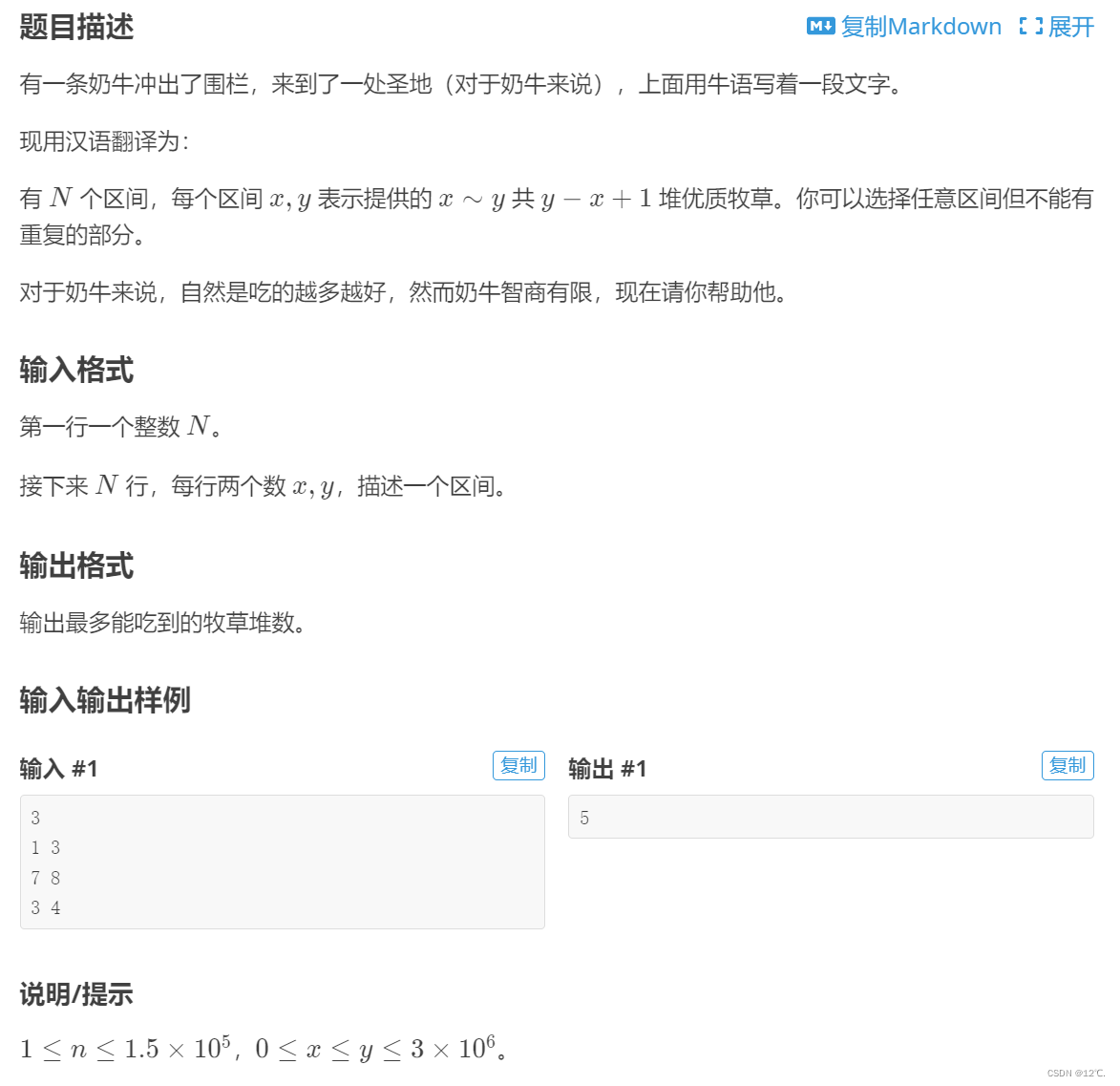
一. 什么是SVM
1. 简介
SVM,曾经是一个特别火爆的概念。它的中文名:支持向量机(Support Vector Machine, 简称SVM)。因为它红极一时,所以关于它的资料特别多,而且杂乱。虽然如此,只要把握住SVM的一些特点,至少可以做到思路清晰。
(1)首先,SVM是按照监督类学习方式进行运作的。即:数据当中含有目标值。
(2)SVM采用监督学习方式,对数据进行二分类(这点跟逻辑回归一样)。但是,SVM和逻辑回归(LR)有有很多不同点。我们先看看相同点:
- 二者都是线性分类器
- 二者都是监督学习算法
- 都属于判别模型(KNN, SVM, LR都属于判别模型),所谓判别模型就是指:通过决策函数,判别各个样本之间的差别来进行分类。
不同点就很多了,现在先列举一些,LR之前已经介绍过,关于SVM的具体理论先放到后面
-
二者的损失函数和目标函数不一样。
-
二者对数据和参数的敏感度不同。SVM由于采用了类似于“过度边界”的方式,泛化能力更好
SVM可以作线性分类器,但是在引入核函数(Kernel Method)之后,也可以进行非线性分类
2.SVM分类
SVM大体上可分为:
- 线性可分SVM:大体就是指一条线,把样本分成两份这种,我们会先从这个入手,这个相关理论懂了,后面的就会很简单
- 线性SVM
- 非线性SVM(需要核函数的支持)
二. 详细介绍
1. 线性可分SVM
1.1 支撑点,支撑向量
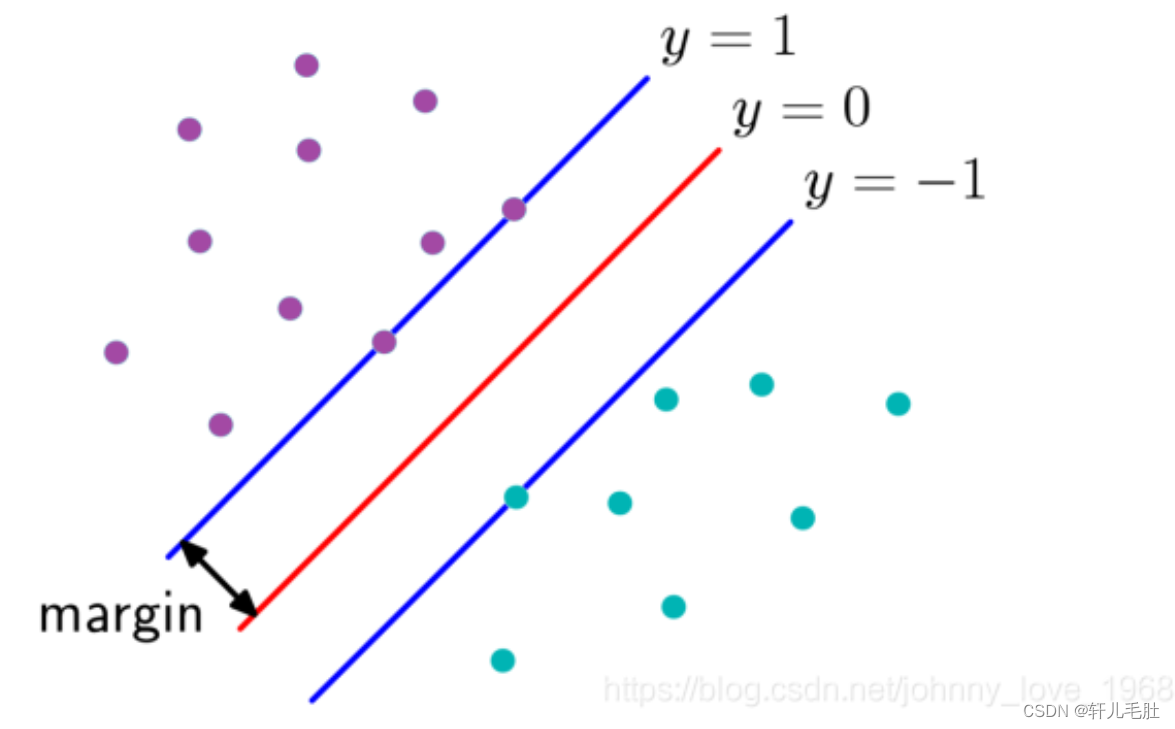
这个将作为重点来理解,这个相关理论知道了,那么,剩下的就很好理解,首先,我们先看一张图,然后我们根据这张图引出两个概念:支撑点,支撑向量。
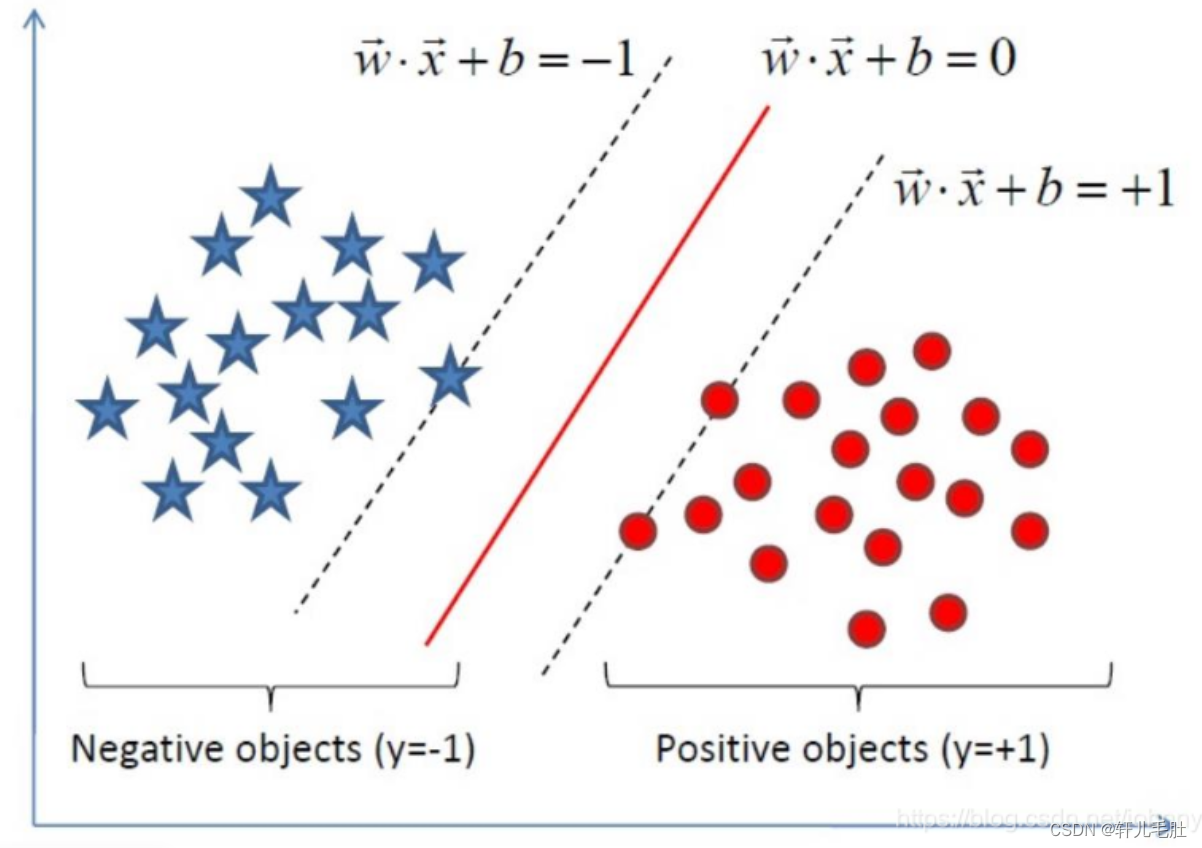 图一
图一
我们看看图上面的三条线,首先,这是个二维平面,因此分割线可以表示成线性函数的形式:
![]()
关于w,它其实是一个权值向量,它可以表示成如下的形式,至于说为什么能够这么表示,我们一会儿再说。

在上图中,两个虚线之间,我们可以当做一个“过度区域”,在虚线上面,有一个蓝色的点,和两个红色的点正好位于虚线上面。对于这3个样本,我们标号1,2,3。我们大可以让alpha1,alpha2, alpha3不为0,其他的点alpha都是0。为什么可以这么做呢?因为边界的划定,也就是虚线,只受这三个边界点的影响(即:影响w向量)我们在现实中直接调整这三个边界点的alpha值,就可以确定界限。那么这三个点,我们就可以称他们为:**支撑点 **
如果你确定了一个起始点,那么起始点到各个点之间可以组成向量,这个起始点到支撑点之间就可以组成一个个:支撑向量
1.2 分割超平面与间隔最大化
首先,我们得知道什么是超平面?一般来说,二维就可以组成一个平面,那么如果是多维的呢?一般把超过二维的,就叫做超平面。由于超平面本身超出了一般人的认知,所以我们在理解分割超平面的时候,还是以最简单的二维平面入手,然后进行扩展。
在了解了什么是超平面之后,我们看这样一个图:

在这幅图中,我们看到了如此多的分割线,这些分割线都成功的把黑点和白点给区分开了。即:都把类别给分对了。那么,哪条线才是最优的呢?(如何分割超平面,就是解决这个问题)
我们就直接在二维空间一个基本问题入手:点到直线的距离入手。
我们假设有这么一条线:
![]()
再给定一个点(x0, y0)那么这个点到直线的距离就是:
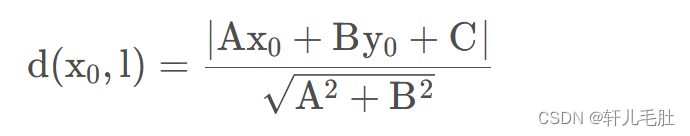
然后我们在此基础上直接把分子的绝对值给去掉,去掉之后,运算结果就会有正负之分了,通过正负,可以判断这个点在这条直线的哪一侧。然后各个项给拆开如下:
![]()
我们令各项系数分别记为:A’, B’ C’。然后整个公式就可以写成向量相乘的形式:
![]()
我们直接把(A’,B’)记为wi向量,将后面的(x0,y0)记为x向量 C’可以记为b,于是就得到了上述式子。
在这个例子当中,只是给了一个二维平面,实际情况下,有可能是多维的。此时w向量也是多维的,可以记为w = (w1,w2,w3……wn),其中这里的w1, w2对应的就是上面式子当中的A, B。我们再回过头看点到直线距离公式,看看那个分母。大致就可以猜出来一件事情:在多维空间中一个点到一个线的距离是: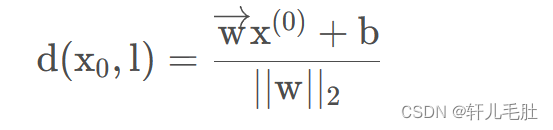
此时,我们再看看图一。注意,图一两条虚线线等号后面分别是+1,-1,为啥是这个呢?
假设我划分了一个线,那么显然,每一个点到这个线都会有一个距离,按照上面这个式子,求出来的距离是带有符号的,这个时候就体现出这个1,-1的价值。这个1,-1,也是y(i)值。如果,求出的是正的,那么乘以1,就是距离本身,如果d为负值,那么乘以-1,又转回正的,还是距离。这就是为什么真正的距离会写成

那么,我所有点,都跟这个直线求一个距离,最后取一个最小值。
我跟所有的直线,都做上面这个操作,就会得到若干个这样的最小值,然后我取最小值最大的那个直线,就是最优解。即:
![]()
对于这个方式,有一个很直观的名字:间隔最大化。
以上就是对分割超平面的一种直观的解释的一个解释。如果扩展到多维,即:超平面,很多时候,我们就不能用单纯一个x向量来解释了。其实,二维当中y与x是线性关系,也是一种映射关系。在多维平面当中,这种映射往往比较复杂,因此,扩展之后,我们会把间隔最大化的线写成如下形式:![]()
其中,φ(x)是某个确定的特征空间转换函数,它的作用是将x映射到(更高的)维度。而在最简单的二维平面中φ(x)=x
由于在线性可分SVM是用来做分类问题,最基本的就是用来做二分类问题,所以,还要把上面这个式子映射到一个只有两个取值的函数当中,这就是线性可分SVM的决策函数:
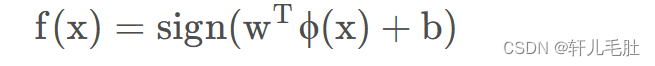
1.3 线性可分SVM的目标函数以及相关算法
我们在图一当中,知道,虚线部分的y值取1,或者-1。但实际上,支撑点可不一定满足这个条件,类似的例子,可以举出无数个。因此,对于目标函数的构建,我们首先就要考虑一个问题:缩放。
根据题设,我们有一个间隔最大化的函数:
![]()
我们要让y(x)满足这个条件:
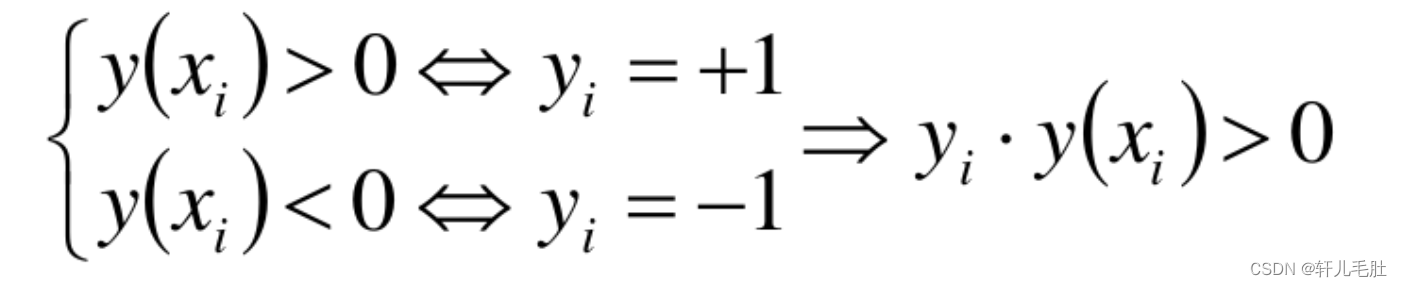
我们对w和b进行等比缩放,就得到了(回过头看看公式(一)):

于是,把这个与公式二结合起来看,我们就得到了目标函数:
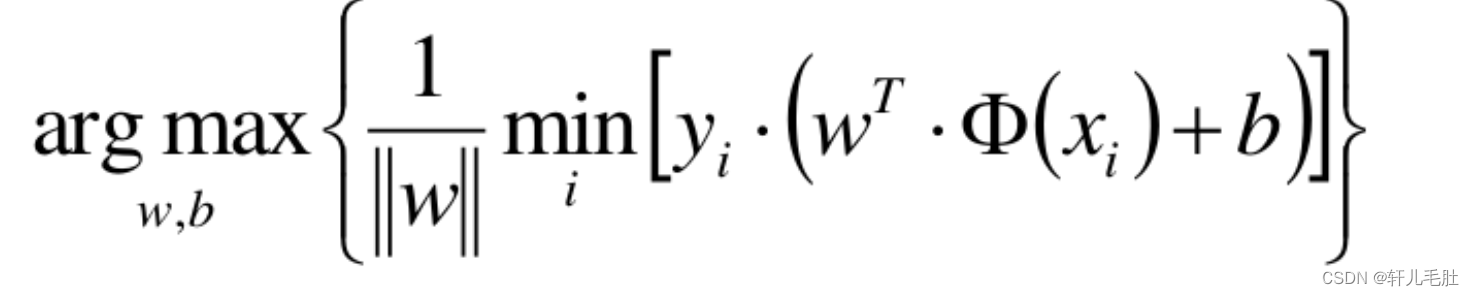
缩放的理论知道了,我们下一步,就是想,怎么能让那个y值是1。对于分类来说,就是让各个类别的点,尽量远离过渡区域,也就是说,这些点离分割线的距离要大于或者等于1,这样才达到分类目的,如下图所示:那个margin大于1,分类才越准确。
用符号表示就是:
通过等比例缩放w的方法,使得两类点的函数值都满足| y |≥1
然后,我们把间隔函数代入:
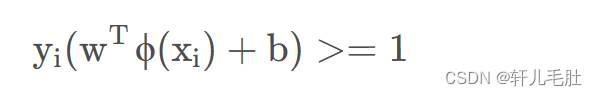





(公式三)
那么,我们就可继续用拉格朗日乘数法进行求解,然后,就求出了alpha*
1.4 线性可分SVM的简单举例
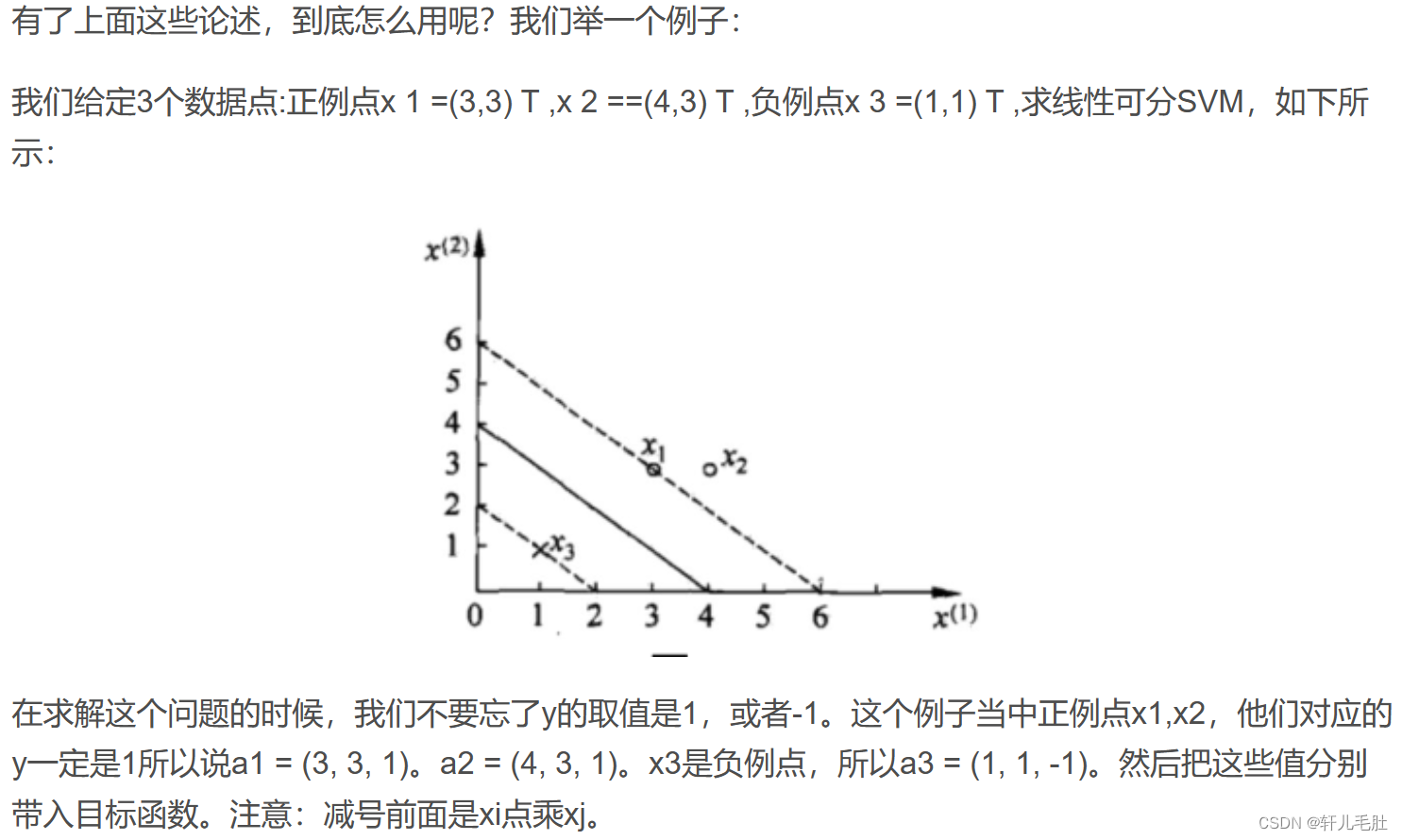


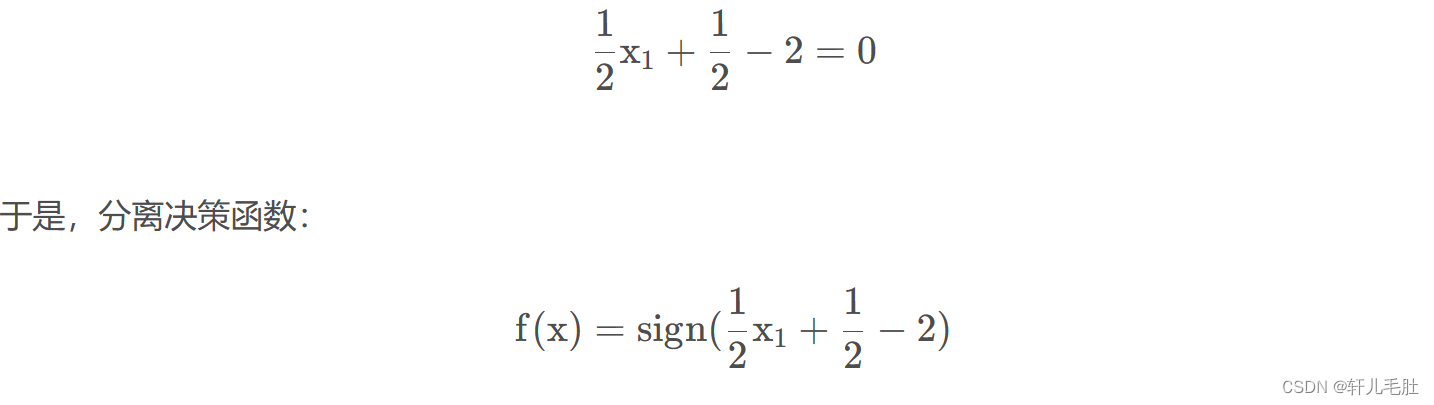
2.线性SVM
2.1 为什么需要线性SVM
在实际运用当中,首先,即使数据是线性可分的。通过线性可分SVM得到的分离超平面也不一定就是最适合的。比如说下面这个图:
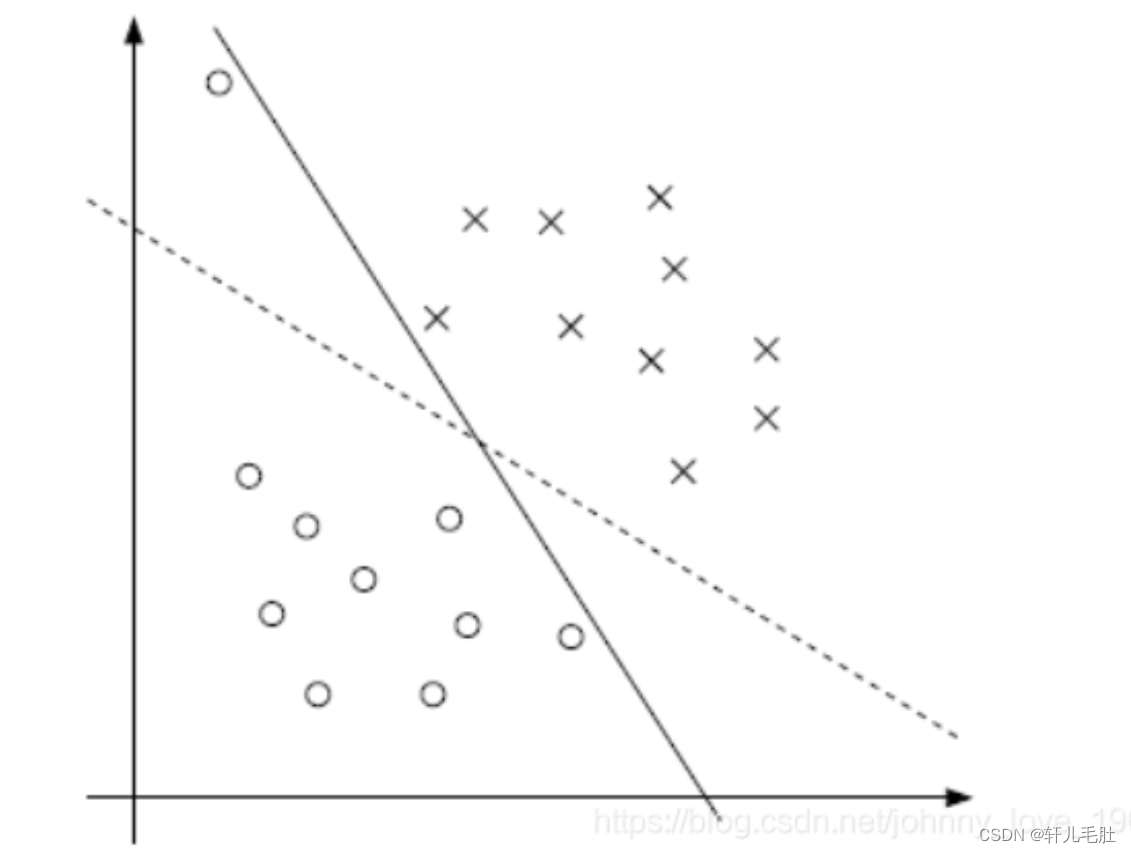
如果按照分割超平面理论,实线应该属于最优的。但是,虚线部分,过渡带比较宽,所以他的泛化能力更好,可以更大可能的避免过拟合。
其次,如果数据根本就不是线性可分(即:线性不可分)的呢?你根本无法通过一条线或面就分的很明白呢?这就是为什么,我们要考虑:线性支持SVM
所谓线性不可分,就是指:一个数据集不可以通过一个线性分类器(直线、平面)来实现分类。这样子的数据集在实际应用中是很常见的,例如:人脸图像、文本文档等。