一、 引言
引言直接从原论文复制,大概看一下论文的关键点:
垂直导向钻井工具在近钻头振动和工具旋转的钻井工作状态下,工具姿态参数的动态测量精度不高。为此,通过理论分析和数值仿真,提出了转速补偿的算法以消除工具旋转对测量的影响; 采用最小均方算法( Least Mean Square—LMS) 自适应滤波算法,可以有效滤除近钻头振动对测量的影响。数值仿真表明,经过转速补偿和LMS 自适应滤波后的井斜角测量误差可小于0. 1°,工具面角测量误差小于6°,有效地提高了垂直导向钻井工具的动态测量精度。
关键点:转速补偿的算法以消除工具旋转对测量的影响;用最小均方算法( Least Mean Square—LMS) 自适应滤波算法,可以有效滤除近钻头振动对测量的影响。
二、 动态测量中的问题
2.1 旋转运动对姿态测量的影响
在实际钻井过程中,设导向工具绕其回转中心以转速ω 旋转,则重力加速度计的工作状态如图1所示,图中R 为加速度计中心O’ 到工具回转中心O的距离。
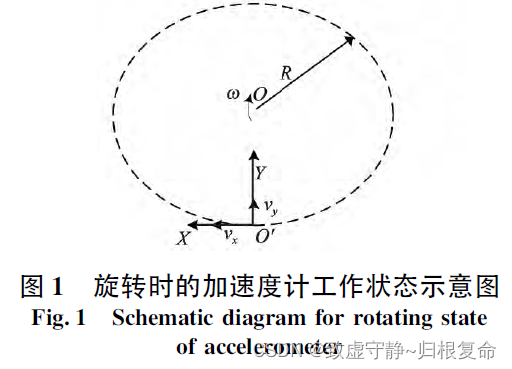
此时,X 轴 将会受到切向的附加惯性力作用,因此作用在X轴加速度计质量块的加速度 a x a_x ax不仅仅是重力加速度分量,还包括切向附加惯性力加速度。由加速度线性叠加原理得: a x = g x + α x = g s i n θ s i n φ + d ω d t R a_x=g_x+\alpha_x=gsin\theta sin\varphi +\frac{d\omega}{dt}R ax=gx+αx=gsinθsinφ+dtdωR
其中, g x g_x gx为X 轴重力加速度分量,单位为 m / s 2 m/s^2 m/s2 ; α x \alpha_x αx为X 轴所受到的切向附加惯性力加速度,单位为 m / s 2 m/s^2 m/s2,它与转速ω 的变化率成正比例; θ 为井斜角、φ 为工具面角。
Y 轴重力加速度计质量块也会因旋转而受到离心力作用,其加速度
a x = g x + α x = g s i n θ s i n φ + ω 2 R a_x=g_x+\alpha_x=gsin\theta sin\varphi +\omega^2R ax=gx+αx=gsinθsinφ+ω2R
其中, g y g_y gy为Y 轴重力加速度分量,单位为 m / s 2 m/s^2 m/s2; α x \alpha_x αx为Y轴所受到的离心力加速度,单位为 m / s 2 m/s^2 m/s2,它与转速平方成正比。由上面两个公式可知,当工具转速较高时,安装在导向工具上的重力加速度计在井眼的不同方位上将产生差异较大的测量信号,从而导致工具姿态的较大测量误差。
2.2 近钻头振动对姿态测量的影响
在正常钻进过程中,钻头切削岩石会使钻柱产生横向和纵向振动,且横向振动尤为明显。近钻头振动信号有3 大特性:
①牙轮钻头牙齿吃入岩石形成高频特性;
②近钻头震源具有宽频性;
③钻头牙齿、牙轮与钻头整体复合运动具有随机性。
近钻头振动信号的幅值一般在10g左右( g 为重力加速度, g = 0.9 m / s 2 g=0.9m/s^2 g=0.9m/s2 ) ,最大可达到30g。因此,近钻头的振动加速度一般远大于重力加速度,弱小的重力加速度信号将湮灭在振动加速度噪声中,导致工具姿态测量无效。根据近钻头横向振动信号特性,采用幅值为6 g 的随机白噪声来模拟近钻头高频随机振动信号,信号特征如下图所示。
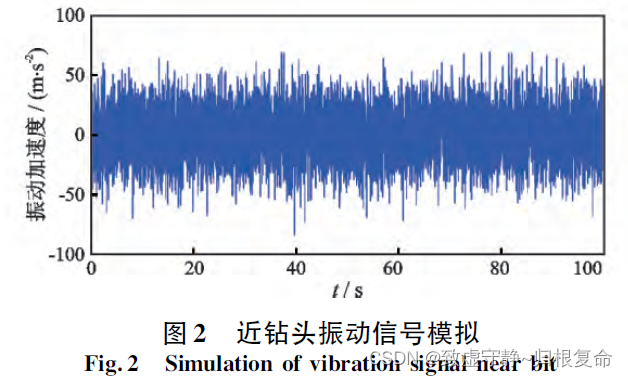
设仅考虑近钻头处的横向振动,其对X、Y 轴向分解后分别记为Ax、Ay,设 A x = K x g A_x=K_xg Ax=Kxg, A y = K y g A_y=K_yg Ay=Kyg; K x 、 K y K_x、K_y Kx、Ky为最大值为10 的随机系数。假设近钻头振动、旋转运动以及重力加速度对加速度计的影响线性可加,则X,Y 轴重力加速度计的测量信号为 V ^ x = V x + V r x + V p x = V g s i n θ s i n φ + V g R g d ω d t + K x V g \hat{V}_x=V_x+V_{rx}+V_{px}=V_gsin\theta sin\varphi +V_g\frac{R}{g}\frac{d\omega}{dt}+K_xV_g V^x=Vx+Vrx+Vpx=Vgsinθsinφ+VggRdtdω+KxVg
V ^ y = V y + V r y + V p y = V g s i n θ c o s φ + V g R g ω 2 + K y V g \hat{V}_y=V_y+V_{ry}+V_{py}=V_gsin\theta cos\varphi +V_g\frac{R}{g}\omega^2+K_yV_g V^y=Vy+Vry+Vpy=Vgsinθcosφ+VggRω2+KyVg
其中: V x 、 V y V_x、V_y Vx、Vy为加速度计的理想输出信号; V r x 、 V r y V_{rx}、V_{ry} Vrx、Vry分别为X、Y 轴加速度计的旋转附加信号; V p x 、 V p y V_{px}、V_{py} Vpx、Vpy为振动产生的附加信号。
三、导向工具姿态动态测量方法
3.1 工具旋转转速补偿算法
考虑到工具旋转时的附加信号 V r x 、 V r y V_{rx}、V_{ry} Vrx、Vry为转速ω的函数,因此,利用速率陀螺仪实时测出工具转速ω,则可进行误差校正。
设由速率陀螺仪测得导向工具转速为 ω ^ \hat{\omega} ω^( 考虑速率陀螺仪的测量误差为5%) ,可计算得工具旋转附加信号估计值为 V ^ r x 、 V ^ r y \hat{V}_{rx}、\hat{V}_{ry} V^rx、V^ry利用2.2节的公式进行校正: V ^ x 1 = V ^ x − V ^ r x = V x + V p x \hat{V}_{x1}=\hat{V}_{x}-\hat{V}_{rx}=V_x+V_{px} V^x1=V^x−V^rx=Vx+Vpx
V ^ y 1 = V ^ y − V ^ r y = V y + V p y \hat{V}_{y1}=\hat{V}_{y}-\hat{V}_{ry}=V_y+V_{py} V^y1=V^y−V^ry=Vy+Vpy
3.2 振动信号的自适应滤波
近钻头振动信号是一种宽带噪声信号,自适应滤波器利用其自动调节参数的优势,无需知道输入信号和噪声统计特性,自动跟踪噪声源,将噪声滤除。自适应滤波的基本思想是: 将振动信号与滤波估计出的参考信号进行抵消操作。
自适应滤波器有两路输入:
一路为原始通道,其不仅接收加速度计测量信号 V x ( k ) V_x(k) Vx(k)( 将加速度传感器测量信号离散化) ,还接收和信号 V x ( k ) V_x(k) Vx(k)不相关的近钻头振动附加信号 V r p 0 ( k ) V_{rp0}(k) Vrp0(k)
另一路为参考输入通道,其接收与信号 V x ( k ) V_x(k) Vx(k)不相关且与振动信号 V r p 0 ( k ) V_{rp0}(k) Vrp0(k)相关的振动信号 V r p 1 V_{rp1} Vrp1
自适应滤波器原理图结构如下所示:
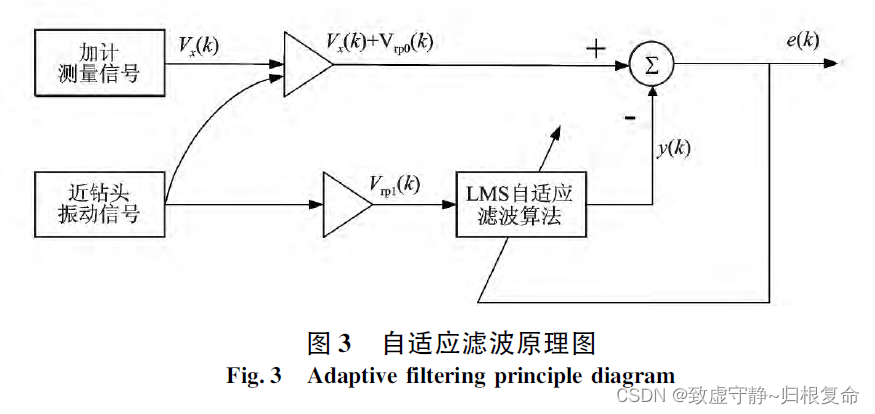
根据自适应滤波器的特性,振动信号 V r p 1 ( k ) V_{rp1}(k) Vrp1(k)经过LMS自适应滤波器自动调整输出后,得到 V r p 1 ( k ) V_{rp1}(k) Vrp1(k)的估计信号,即 y ( k ) = V ^ r p 1 ( k ) y(k)=\hat{V}_{rp1}(k) y(k)=V^rp1(k).
则自适应滤波器系统输出的误差信号e( k) 等于原始信号和参考输入信号的差值,表示为: e ( k ) = V x ( k ) + V r p 0 ( k ) − V ^ r p 1 ( k ) e(k)=V_x(k)+V_{rp0}(k)-\hat{V}_{rp1}(k) e(k)=Vx(k)+Vrp0(k)−V^rp1(k)
对这个式子做一个变形: e ( k ) − V x ( k ) = V r p 0 ( k ) − V ^ r p 1 ( k ) e(k)-V_x(k)=V_{rp0}(k)-\hat{V}_{rp1}(k) e(k)−Vx(k)=Vrp0(k)−V^rp1(k)
并且对上面的两边同时开平方并取均方误差: E [ e 2 ( k ) ] = E [ V x 2 ( k ) ] + E [ ( V r p 0 ( k ) − V r p 1 ( k ) ) 2 ] + 2 E [ V x ( K ) ( V r p ( k ) − V r p 1 ( k ) ) ] E[e^2(k)]=E[{V_x}^2(k)]+E[(V_{rp0}(k)-V_{rp1}(k))^2]+2E[V_x(K)(V_{rp}(k)-V_{rp1}(k))] E[e2(k)]=E[Vx2(k)]+E[(Vrp0(k)−Vrp1(k))2]+2E[Vx(K)(Vrp(k)−Vrp1(k))]
E [ e 2 ( k ) ] E[e^2(k)] E[e2(k)]表示功率信号, V x ( k ) V_x(k) Vx(k)与 V r p 1 ( k ) V_{rp1}(k) Vrp1(k)无关,所以 2 E [ V x ( K ) ( V r p ( k ) − V r p 1 ( k ) ) ] = 0 2E[V_x(K)(V_{rp}(k)-V_{rp1}(k))]=0 2E[Vx(K)(Vrp(k)−Vrp1(k))]=0,因此, 均方误差 E [ e 2 ( k ) ] E[e^2(k)] E[e2(k)] 最小, 等价于 E [ ( V r p 0 ( k ) − V r p 1 ( k ) ) 2 ] E[(V_{rp0}(k)-V_{rp1}(k))^2] E[(Vrp0(k)−Vrp1(k))2]达到最小。
LMS 自适应滤波过程是由其权向量迭代公式: W ( k + 1 ) = W ( k ) + 2 μ e ( k ) x ( k ) W(k+1)=W(k)+2\mu e(k)x(k) W(k+1)=W(k)+2μe(k)x(k)
自身调节权值 W ( k ) W(k) W(k)使得 E [ e 2 ( k ) ] E[e^2(k)] E[e2(k)]达到最小。
式中: μ \mu μ为调整搜索步长的正值常数,其收敛速度与系统稳定性有关; W ( k ) W(k) W(k)为系统第k 次迭代权系数; x ( k ) x(k) x(k)为输入信号。
根据 e ( k ) − V x ( k ) = V r p 0 ( k ) − V ^ r p 1 ( k ) e(k)-V_x(k)=V_{rp0}(k)-\hat{V}_{rp1}(k) e(k)−Vx(k)=Vrp0(k)−V^rp1(k),所以在LMS 准则下, E [ ( V r p 0 ( k ) − V r p 1 ( k ) ) 2 ] E[(V_{rp0}(k)-V_{rp1}(k))^2] E[(Vrp0(k)−Vrp1(k))2]被最小化的同时, E [ ( V r p 0 ( k ) − V r p 1 ( k ) ) 2 ] E[(V_{rp0}(k)-{V}_{rp1}(k))^2] E[(Vrp0(k)−Vrp1(k))2]也被最小化了,即LMS 自适应滤波器的输出 y ( k ) y(k) y(k) 向 V r p 1 ( k ) V_{rp1}(k) Vrp1(k)逼近等效于 e ( k ) e(k) e(k) 向 V x ( k ) V_x(k) Vx(k) 逼近,从而系统输出的是加速度计信号 V x ( k ) V_x(k) Vx(k)的最佳估计。
剩下的内容为效果仿真了,具体就不再看了,论文整体上思路很简单,也好理解,细心看一下就好,而且本篇论文实际稍微有点远,为2016的论文,有兴趣的可以从知网下载。
四、往期回顾
课题学习(一)----静态测量
课题学习(二)----倾角和方位角的动态测量方法(基于磁场的测量系统)
课题学习(三)----倾角和方位角的动态测量方法(基于陀螺仪的测量系统)
课题学习(四)----四元数解法
课题学习(五)----阅读论文《抗差自适应滤波的导向钻具动态姿态测量方法》
课题学习(六)----安装误差校准、实验方法
课题学习(七)----粘滑运动的动态算法
课题学习(八)----卡尔曼滤波动态求解倾角、方位角




![[动态规划] (一) LeetCode 1137.第N个泰波那契数](https://img-blog.csdnimg.cn/img_convert/5a82e2bb09145e8ed83c3ae14771c6fa.png)