2017年亚太杯APMCM数学建模大赛B题喷雾轨迹规划问题求解全过程文档及程序

2017年亚太杯APMCM数学建模大赛

B题喷雾轨迹规划问题

原题再现

喷釉工艺用喷釉枪或喷釉机在压缩空气下将釉喷入雾中，使釉附着在泥体上。这是陶瓷生产过程中一个容易实现自动化的过程。由于不均匀的釉料在烧制过程中会产生裂纹，导致工件报废，因此要求喷涂过程中喷涂的釉料厚度尽可能均匀。

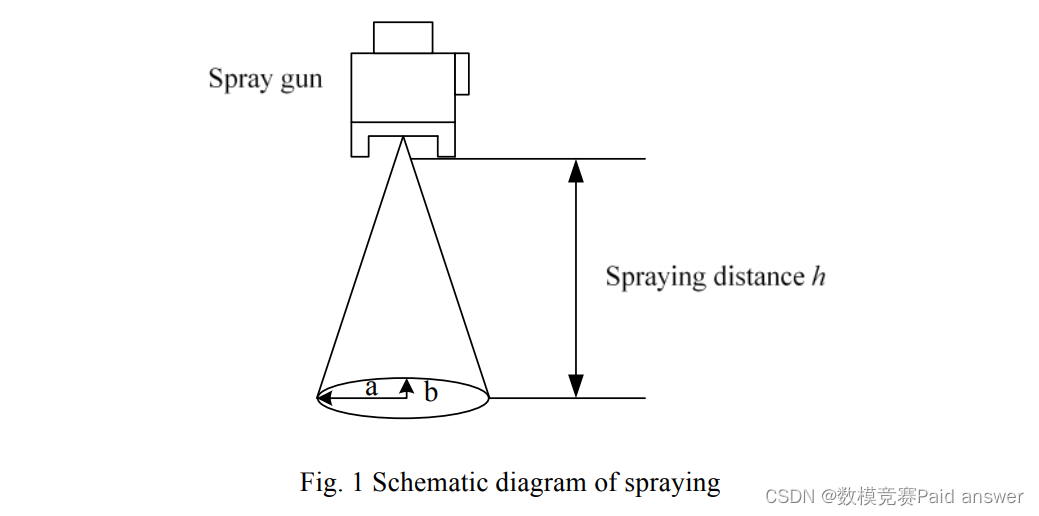
在实际的空气喷涂中，压缩空气通常布置在喷枪嘴的两侧，雾锥被挤压成椭圆锥，漆雾形成的喷雾锥覆盖的平面上的区域是椭圆，半长轴为a，半短轴为b，如图1所示。
在这里插入图片描述
它在椭圆分布区域中满足椭圆双β分布模型：

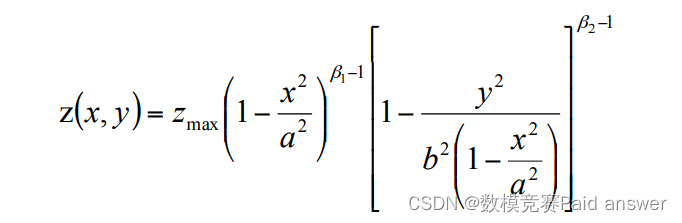
式中：a——喷淋椭圆半长轴（mm）；b——喷淋椭圆的半短轴（mm）；maxz——漆膜最大厚度；β1−x方向截面β分布指数；β2−y方向截面中β分布的指数。
有研究表明，雾化压力P1、隔膜泵压力P2和喷雾距离h是影响上述参数的主要因素，它们之间的关系如下：
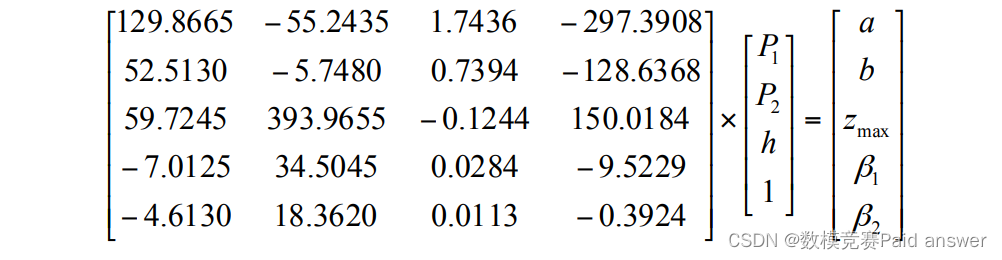
在这里插入图片描述
上述模型为单点喷枪喷涂模型。然而，在实践中，喷枪需要沿着计划的路径移动，以便要喷涂的工件表面均匀地覆盖釉，如图2所示。

由于单点喷涂时，雾锥区域厚度中间偏大，两侧偏薄，为保证喷涂表面均匀，雾锥将在图3中相邻路径重叠。
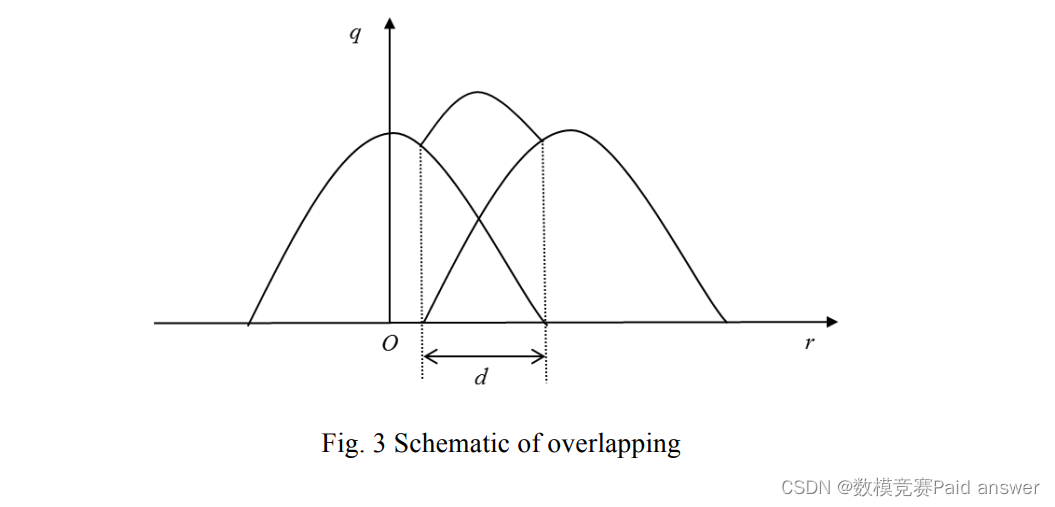
在这里插入图片描述
基于上述背景，我们尝试探讨以下四个问题：

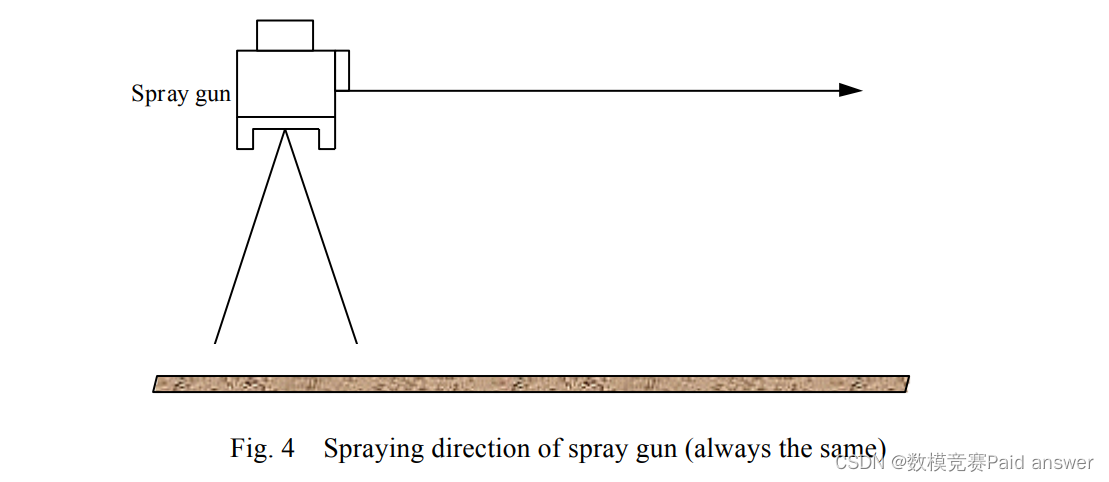
1、根据以上资料，如果喷枪的喷涂方向始终保持不变（如图4所示），请计算平面内喷涂的累积情况，找出喷枪轨迹的合适重叠间隔（P1和P2取0.2Mpa，h取225mm）。
在这里插入图片描述
2、对于曲面z=−x~2+x−xy（−10≤x≤10，−10≤y≤10），确定问题1中计算的喷涂间隔是否适用。如果没有，请重新规划喷枪轨迹，并计算重叠间隔，使釉面厚度差小于10%（不同轨迹的间隔可以不同，P1和P2取0.2Mpa，h可根据实际需要选择）。

3、喷涂过程中，如果喷枪的喷涂方向始终是雾锥中心（如图5所示）喷涂点的法线方向，其他条件不变，请重新计算问题2的结果。
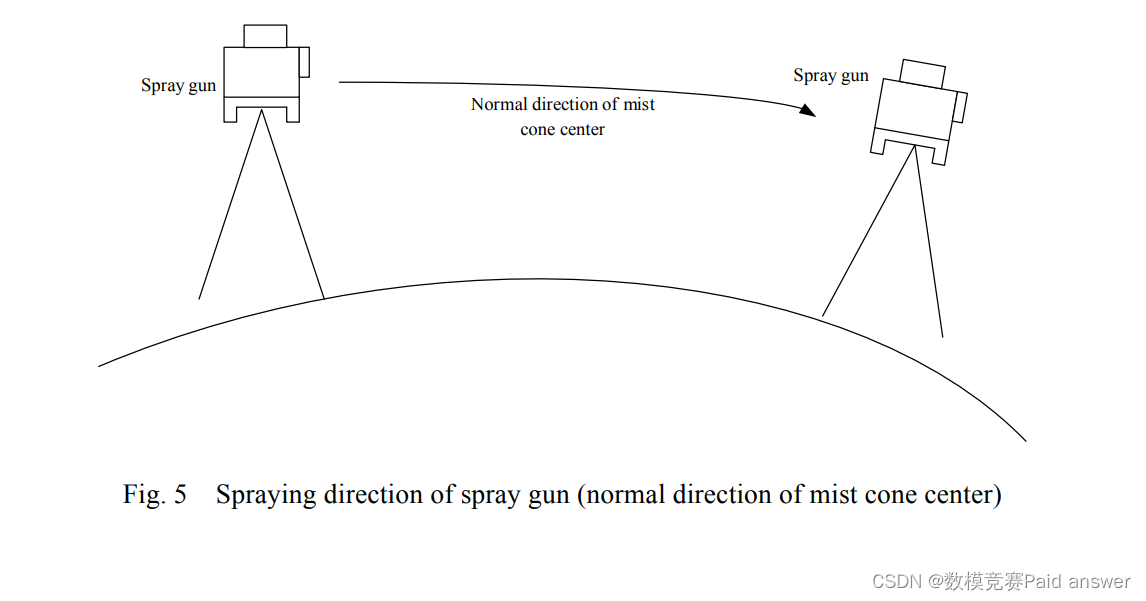
在这里插入图片描述
4、问题3的结果是否适用于任何曲面z=f（x，y）？喷涂路径规划是否有通用解决方案

整体求解过程概述(摘要)

机器人上釉作为提高陶瓷生产过程自动化程度的一种新方法，对提高上釉效率有一定的作用。因此，探索机器人釉料在不同工件表面条件下的自动轨迹规划对提高陶瓷工艺现代化水平具有重要意义。

平面釉料自动轨迹规划：首先，将微积分法与椭圆双β分布模型相结合，建立以釉料厚度均匀性为目标的平面釉料轨迹优化模型。最后，对不同横截面的釉膜厚度模型进行仿真分析，验证了模型的正确性。

曲面（垂直于水平方向）施釉轨迹规划：首先，采用投影法对椭圆双β分布模型进行修正，得到施釉方向垂直于水平方向时曲面的釉膜厚度分布模型

确定方向。然后，建立曲面轨道优化模型，对最小釉厚差进行优化。最后证明了问题1的重叠区间不适用于问题2的曲面，问题2的重叠区间d的最优解为89.36～95.05mm。

曲面（沿喷点法向）施釉轨迹规划：首先采用投影法修正平面椭圆双β分布模型，建立喷釉方向为雾锥中心喷点法向时的釉膜厚度分布模型。然后，基于切片算法，以涂层均匀性为优化目标，建立了表面喷釉轨迹优化模型。最后证明了曲面重叠间隔d的最优解为80.26～90.53mm。

任意曲面釉面轨迹规划：首先利用β角、θ角、喷枪高度等参数描述不同曲面之间的差异。通过改变不同的地面观测参数，重复发射装置的参数。最后，采用黄金分割迭代法求出d值，并编制了任意面釉轨迹规划程序。通过MATLAB仿真验证了模型的正确性，结果符合标准。

模型假设：

➢ 边缘厚度对喷涂层厚度分布模型没有影响。

➢ 喷涂机器人喷涂一定高度，不改变。

➢ 机器人在涂布过程中的速度恒定，没有突变。

问题重述：

问题背景

喷釉是陶瓷生产工艺的重要组成部分，由于釉面不均匀在烧成过程中会产生裂纹，导致零件报废，因此喷釉工艺要求喷釉尽可能厚，同时也降低了效率。

机器人上釉的出现为提高上釉效率提供了一条新途径，对提高陶瓷生产过程的自动化具有重要意义。

我们的工作

➢ 分析了机器人喷釉的平面釉厚度分布，设计了平面釉自动轨迹优化方案。

➢ 探讨了机器人搪瓷上釉方向与水平方向垂直时曲面上釉膜厚度的分布情况，建立了该条件下曲面上釉的自动轨迹优化方案。

➢ 研究了沿锥体法向喷涂的锥体曲面上釉膜厚度的分布。建立了该条件下表面施釉自动轨迹的优化方案。

➢ 探究工件表面是否为任意曲面，是否有通用的自动喷釉机器人优化方案来解决喷釉路径规划问题。

模型的建立与求解整体论文缩略图

在这里插入图片描述

全部论文及程序请见下方“ 只会建模 QQ名片” 点击QQ名片即可

程序代码：

部分程序如下:

[x,y]=meshgrid(-10:1:10);
z=-x.^2+x-x.*y;
mesh(x,y,z);
title('curved surface z')
xlabel('X');
ylabel('Y');
zlabel('Z');

[x,y]=meshgrid(-10:1:10);
z=-x.^2+x-x.*y;
mesh(x,y,z);
title('curved surface z')
xlabel('X');
ylabel('Y');
zlabel('Z');
hold on
ezmesh('0')

A=[129.8665 -55.2435 1.7436 -297.3908;52.5130 -5.7480 0.7394 -128.6368;59.7245 393.9655 -0.1244 150.0184;-7.0125 34.5045 0.0284 -9.5229;-4.6130 18.3620 0.0113 -0.3924];
B=[0.2 0.2 225 1];
C=A*B'
a=C(1);
b=C(2);
Zmax=C(3);
beta1=C(4);
beta2=C(5);
Zmin1=Zmax*(1-(a^2/b^2))^(beta2-1);
y1=sqrt((b^2)*(1-exp((1/(beta2-1))*log((Zmax-Zmin1)/Zmax))));
d1=abs(a-y1);
Zmin2=Zmax*(1-b^2/a^2)^(beta1-1);
x2=sqrt((a^2)*(1-exp((1/(beta1-1))*log((Zmax-Zmin2)/Zmax))));
d2=abs(b-x2);

A=[129.8665 -55.2435 1.7436 -297.3908;52.5130 -5.7480 0.7394 -128.6368;59.7245 393.9655 -0.1244 150.0184;-7.0125 34.5045 0.0284 -9.5229;-4.6130 18.3620 0.0113 -0.3924];
B=[0.2 0.2 225 1];
C=A*B';
a=C(1);
b=C(2);
Zmax=C(3);
beta1=C(4);
beta2=C(5);
Zmin1=Zmax*(1-(a^2/b^2))^(beta2-1);
y1=sqrt((b^2)*(1-exp((1/(beta2-1))*log((Zmax-Zmin1)/Zmax))));
d1=abs(a-y1);
Zmax=C(3);
Z1=Zmax
z=-1+1-(a-d1+1);
h1=0-z;
h=B(3)+h1;
B1=[0.2 0.2 h 1];
C1=A*B1';
a1=C1(1);
b1=C1(2);
Zmax=C1(3);
beta1=C1(4);
beta2=C1(5);
Z2=Zmax*(1-1/a1^2)^(beta1-1)*(1-(a-d1+1)^2/(b1^2*(1-1/a1^2)))^(beta2-
1);
if Z1==Z2fprintf('the overlap interval is suitable')
elsefprintf('the overlap interval isn’t suitable')
end