Chaikin算法——计算折线对应的平滑曲线坐标点

本文将介绍一种计算折线对应的平滑曲线坐标点的算法。该算法使用Chaikin曲线平滑处理的方法，通过控制张力因子和迭代次数来调整曲线的平滑程度和精度。通过对原始点集合进行切割和插值操作，得到平滑的曲线坐标点集合。实验结果表明，该算法能够有效地平滑折线，并且具有较高的精度和可控性。

引言

在计算机图形学和数据可视化领域，平滑曲线的生成是一个重要的问题。平滑曲线可以使得数据更加易于理解和分析，同时也可以提高图形的美观性。折线是一种常见的曲线表示方法，但是折线本身具有较高的噪声和锯齿状的特点，需要进行平滑处理。本文提出了一种基于Chaikin曲线平滑处理的算法，可以将折线转化为平滑的曲线。

---

算法

算法流程

流程的具体步骤如下：

1. 检查输入的坐标点集合的合法性，确保至少有3个坐标点。
2. 对输入的参数进行范围约束，确保迭代次数大于等于1，张力因子在0到1之间。
3. 将张力因子映射到0.05到0.45之间，以便在计算切割距离时使用。
4. 迭代计算，使用Chaikin曲线平滑处理的方法对坐标点集合进行处理。
5. 返回平滑后的曲线坐标点集合。

        /// <summary>/// 计算折线对应的平滑曲线坐标点/// </summary>/// <param name="points">坐标集合</param>/// <param name="tension">张力因子[0,1]，用于控制曲线的平滑程度。张力因子越小时切割点会越靠近线段的起始点，反之会靠近线段的结束点。</param>/// <param name="iterationCount">迭代次数，用于控制曲线平滑的精度</param>/// <returns></returns>/// <exception cref="ArgumentException"></exception>private List<Point> SmoothCurveChaikin(Point[] points, float tension = 0.5f, byte iterationCount = 1){// 坐标点合法性检查if (points == null || points.Length < 3){throw new ArgumentException("至少需要3个坐标点。", nameof(points));}// 参数范围约束iterationCount = Math.Max(iterationCount, (byte)1);tension = Math.Max(tension, 0);tension = Math.Min(tension, 1);// 参数的限制在0到1之间是为了简化参数的使用和理解。将张力因子的取值范围映射到0到1之间，使得参数的范围更加直观和易于控制。// 通过将张力因子乘以0.4并加上0.05，可以将0到1之间的参数映射到0.05到0.45之间，以便在计算切割距离时使用。// 张力因子在这里用于控制曲线的平滑程度。具体来说，张力因子定义了线段半长切角距离的一个尺度，取值范围在0.05到0.45之间。// 当张力因子为0.5时，相当于使用了经典的Chaikin算法，即将每个线段切割成四分之一和四分之三的两个点。这样可以保持曲线的对称性。double cutdist = 0.05 + (tension * 0.4);// 迭代计算List<Point> lst = points.ToList();for (int i = 1; i <= iterationCount; i++){lst = SmoothChaikin(lst, cutdist);}return lst;}

Chaikin曲线平滑处理

Chaikin曲线平滑处理是一种基于切割和插值的方法，通过对线段进行切割和插值操作，得到平滑的曲线。

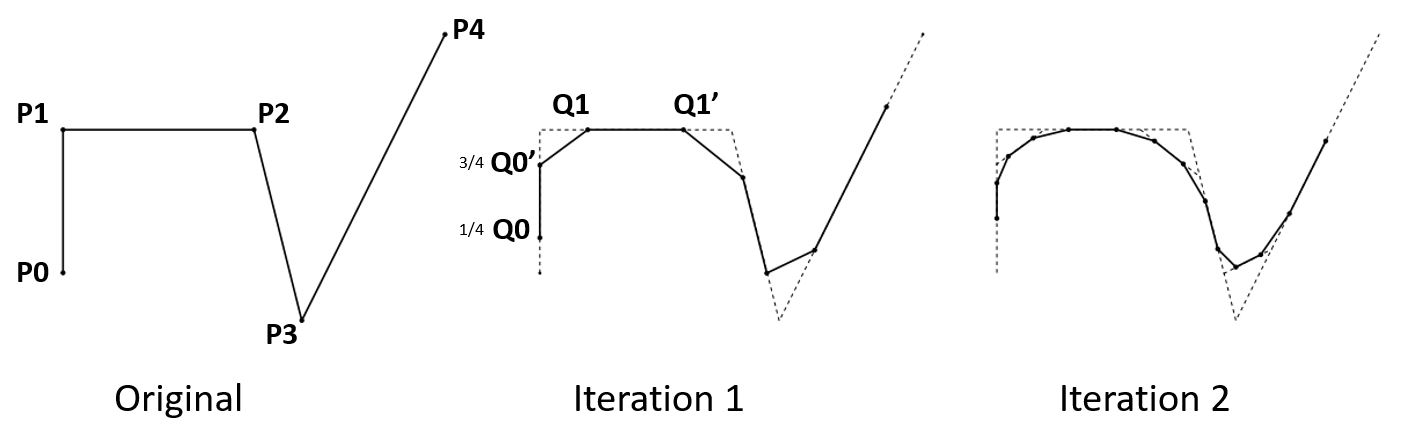
具体步骤如下：

1. 添加第一个点，即原始点集合的第一个点。
2. 将每一个点拆分成前后两个点，通过计算切割距离参数和原始点的坐标进行插值计算。
3. 添加插值计算得到的两个点。
4. 添加最后一个点，即原始点集合的最后一个点。
5. 返回平滑后的曲线坐标点集合。

        /// <summary>/// 对点集合进行Chaikin曲线平滑处理/// </summary>/// <param name="points">要进行平滑处理的曲线的原始点</param>/// <param name="cuttingDist">切割距离参数，用于定义线段切割的尺度。取值范围通常在0.05到0.45之间，用于控制曲线的平滑程度</param>/// <returns></returns>private List<Point> SmoothChaikin(List<Point> points, double cuttingDist){// 添加第一个点List<Point> nl = new List<Point> { points[0] };// 将每一个点拆分成前后两个点Point q, r;for (int i = 0; i < points.Count - 1; i++){q = new Point((int)Math.Round(((1 - cuttingDist) * points[i].X + cuttingDist * points[i + 1].X)),(int)Math.Round(((1 - cuttingDist) * points[i].Y + cuttingDist * points[i + 1].Y)));r = new Point((int)Math.Round((cuttingDist * points[i].X + (1 - cuttingDist) * points[i + 1].X)),(int)Math.Round((cuttingDist * points[i].Y + (1 - cuttingDist) * points[i + 1].Y)));nl.Add(q);nl.Add(r);}// 添加最后一个点nl.Add(points.Last());return nl;}

---

实验与结果

为了验证算法的有效性和可靠性，我们进行了两组测试。

测试1：验证不同迭代次数下的算法结果

测试步骤：

1. 将张力因子设置为0.5。
2. 调整迭代次数为1、2、3。
3. 对比不同迭代次数下的算法结果。

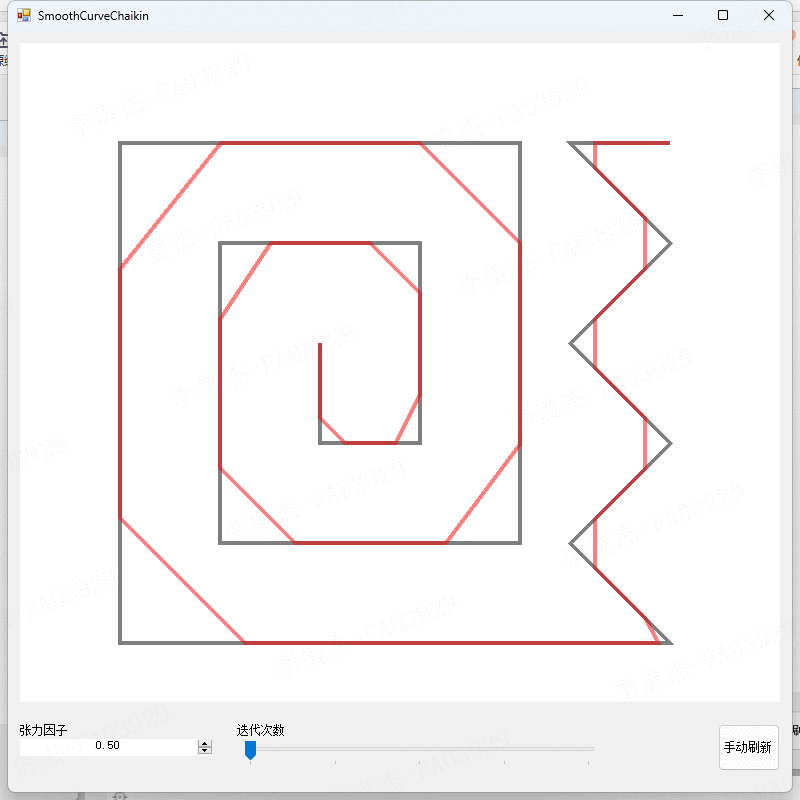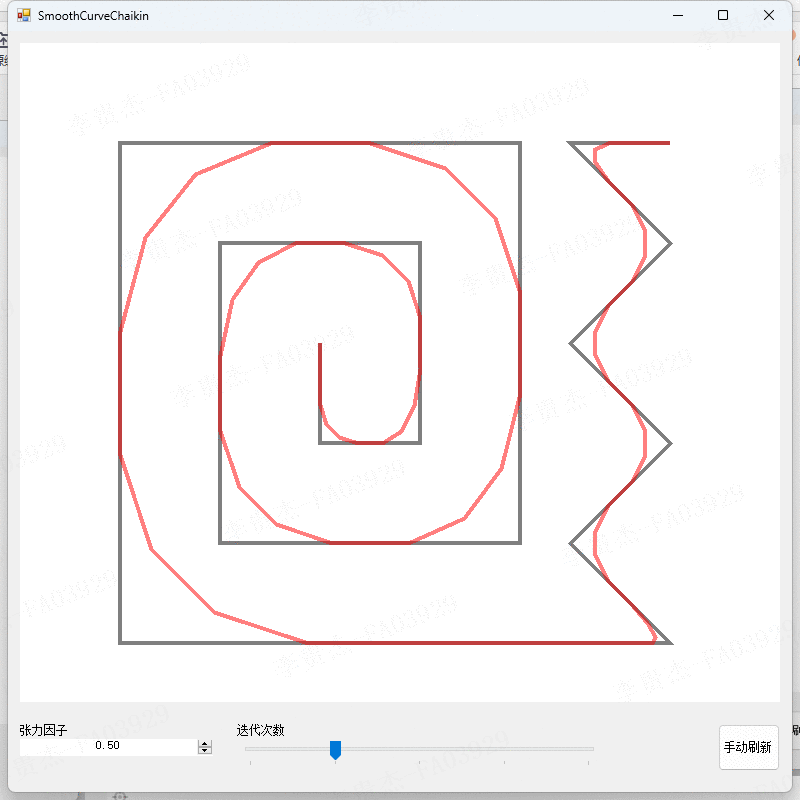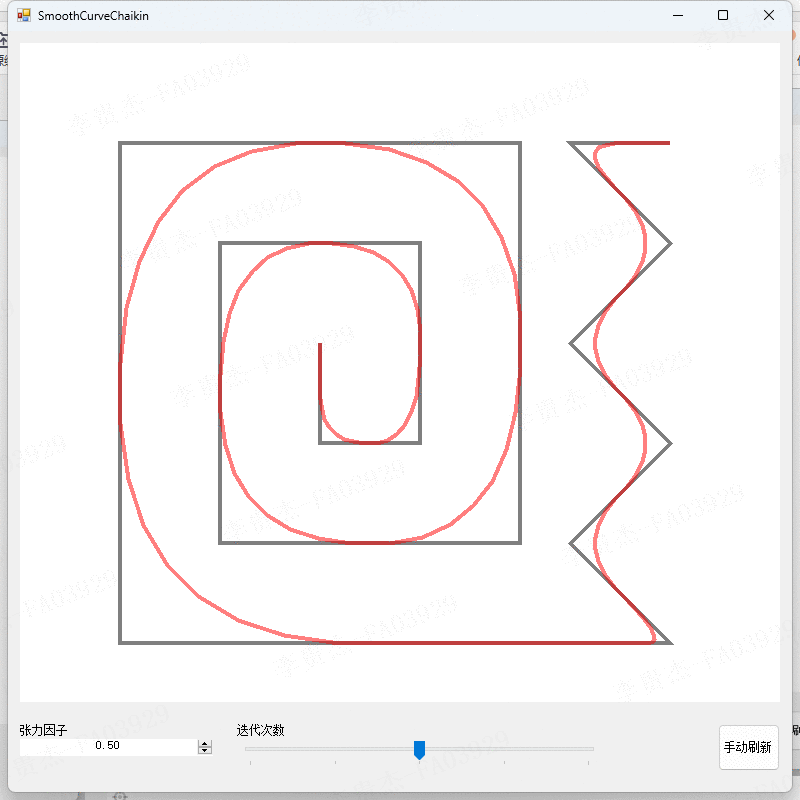
测试2：观察不同张力因子下的算法结果

测试步骤：

1. 将迭代次数设置为1。
2. 调整张力因子为0、0.2、0.4、0.6、0.8。
3. 观察不同张力因子下的算法结果。
   

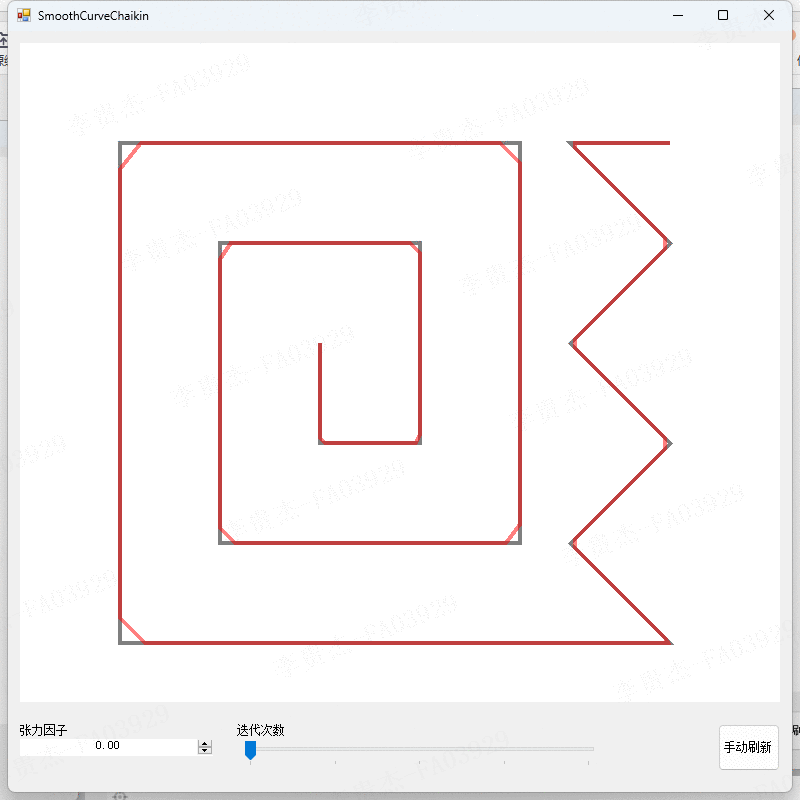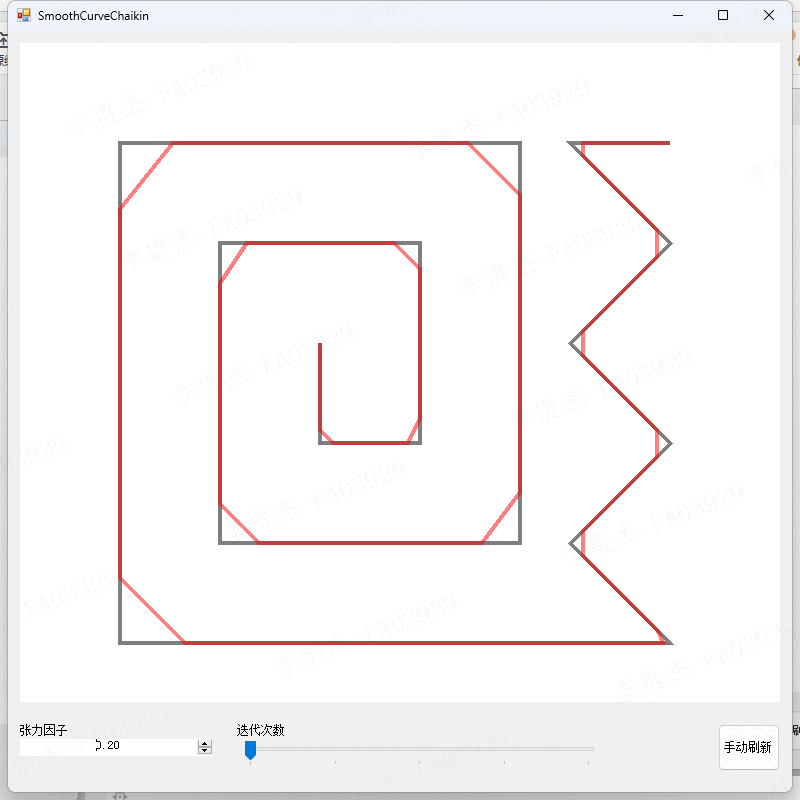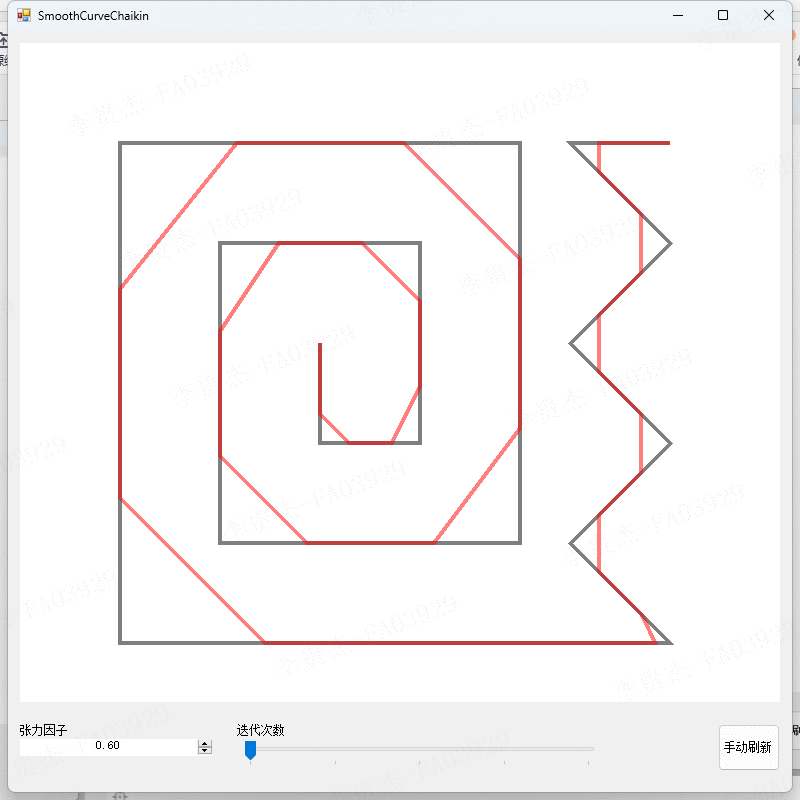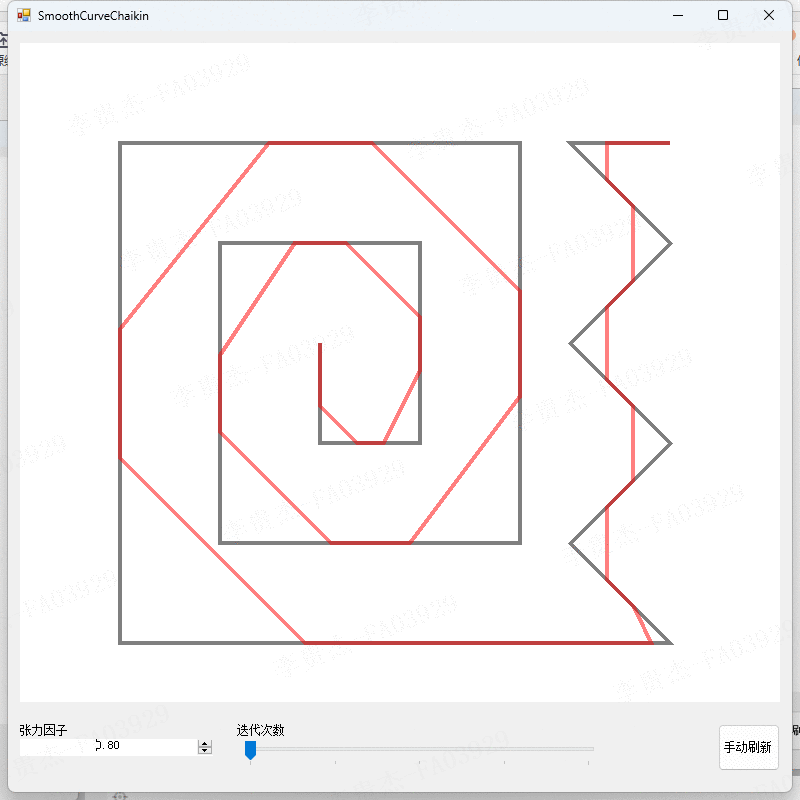
本算法在不同的参数设置下进行了实验，得到了不同平滑程度和精度的曲线。实验结果表明，当张力因子较小时，切割点会靠近线段的起始点，曲线的平滑程度较低；当张力因子较大时，切割点会靠近线段的结束点，曲线的平滑程度较高。迭代次数的增加可以提高曲线的平滑精度，但也会增加计算的时间复杂度。实验结果还表明，本算法能够有效地平滑折线，并且具有较高的精度和可控性。

---

结论

本文介绍了一种计算折线对应的平滑曲线坐标点的算法。该算法使用Chaikin曲线平滑处理的方法，通过控制张力因子和迭代次数来调整曲线的平滑程度和精度。实验结果表明，该算法能够有效地平滑折线，并且具有较高的精度和可控性。未来的工作可以进一步优化算法的性能和扩展算法的应用范围。

---

参考资料

1. 2D Polyline Vertex Smoothing