统计学习方法 决策树

阅读李航的《统计学习方法》时，关于决策树的笔记。

决策树模型与学习

决策树：树状的模型，其中内部节点表示一个特征或属性，叶子节点表示一个类。使用决策树分类时：

• 从根结点出发，对实例的某一特征进行测试，根据测试结果分配到某一叶节点中；
• 重复，直到到达叶子节点；

决策树可以看成是 if-then 规则的集合，也可以看成是对特征空间进行划分的条件概率分布：

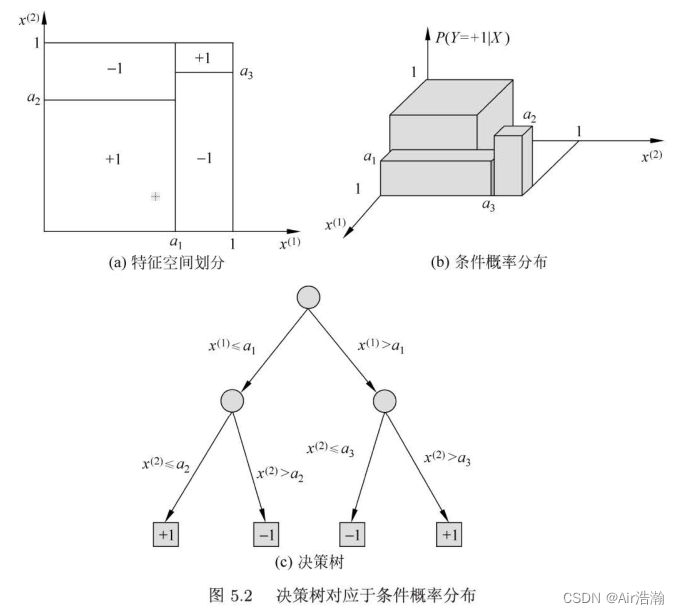
决策树的学习：给定训练集：
D = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , ⋅ , ( x N , y N ) } D=\set{(x_1,y_1),(x_2,y_2),\cdot,(x_N,y_N)} D={(x1​,y1​),(x2​,y2​),⋅,(xN​,yN​)}
其中 $x_i=(x_i^{(1)},x_i^{(2)},\cdots ,x_i^{(n)})$ 为输入实例（特征向量）， y i ∈ { 1 , 2 , ⋯ , K } y_i\in\set{1,2,\cdots,K} yi​∈{1,2,⋯,K} 为类标记。

决策树的学习是从训练数据集中归纳出一组分类规则。但与数据集不相矛盾的决策树往往有很多，在定义好损失函数的情况下，从所有可能的决策树中选取最优的决策树是 NP 完全问题。所以决策树的学习算法通常采用启发式方法，学习到次最优的决策树。

决策树的学习算法通常是对当前训练集，递归地选择某个/些最优特征，并根据特征对训练数据集进行分割。特征选择好和树的深度较深的情况下，在训练集上表现较好，但不一定具有很好的泛化能力，即可能发生过拟合现象。此时我们需要对已生成的树进行从下而上的剪枝。

因此，决策树的学习算法包括：特征选择、决策树的生成和决策树的剪枝过程。

特征选择

我们每一步选择特征，是为了能够将不同类别的实例尽可能分开。特征选择的准则是信息增益和信息增益比。

熵（entropy）：表示随机变量不确定性的度量，设 $X$ 是一个有限取值个数的离散型随机变量，其概率分布为：
$$P(X=x_i)=p_i,i=1,2,\cdots ,n$$
则随机变量 $X$ 的熵定义为：
$$H(X)=-\sum _{i=1}^n{p}_i\log p_i$$

• 定义 $0\log 0=0$ ；

• 对数取 $2$ 或 $\text{e}$ 为底，此时熵的单位分别成为比特（bit）或纳特（nat）；

可以看出熵与 $X$ 的取值无关，只与概率分布有关，因此关于 $X$ 的熵也可以记作 $H(p)$ 。

熵越大，随机变量的不确定性就越大，可以得到：
$$0\le H(p)\le \log n$$
条件熵：两个随机变量 $X$ 和 $Y$ ，条件熵 $H(Y|X)$ 表示已知随机变量 $X$ 的条件下随机变量 $Y$ 的不确定性，定义为：
$$H(Y|X)=\sum _{i=1}^n{p}_{i}H(Y|X=x_i)$$
当熵和条件熵由数据估计（特别是极大似然估计）得到时，分别被称为经验熵（empirical entropy）和经验条件熵。就是说，我们往往不知道数据的概率分布，而只能从训练集中估计出概率分布（比如以类别所占比例作为该类别出现的概率，即极大似然估计法），所以我们算的熵往往都是经验熵。

信息增益：表示得知特征 $X$ 的信息而使得类 $Y$ 的信息的不确定性减少的程度。定义为：特征 $A$ 对训练集 $D$ 的信息增益 $g(D,A)$ 为：
$$g(D,A)=H(D)-H(D|A)$$
熵 $H(Y)$ 与条件熵 $H(Y|X)$ 之差也称为互信息。决策树中信息增益等价于训练数据集中类与特征的互信息。

信息增益的算法：设训练集为 $D$ ，样本容量为 $|D|$ ；假设有 $K$ 个类 $C_k$ ，$|C_k|$ 为属于类 $C_k$ 的样本个数。假设特征 $A$ 有 $n$ 个不同的取值 { a 1 , a 2 , ⋯ , a n } \set{a_1,a_2,\cdots,a_n} {a1​,a2​,⋯,an​}，将训练集分为 { D 1 , D 2 , ⋯ , D n } \set{D_1,D_2,\cdots,D_n} {D1​,D2​,⋯,Dn​} 。记子集 $D_i$ 中属于类 $C_k$ 的样本的集合为 $D_{ik}$ ，即 $D_{ik}=D_i\cap C_k$ 。有：

• 输入：训练集 $D$ 和特征 $A$ ；
• 输出：特征 $A$ 对于训练集 $D$ 的信息增益 $g(D,A)$ ；

1. 计算 $D$ 的经验熵 $H(D)$ ：

$$H(D)=-\sum _{k=1}^K\frac{|C_k|}{|D|}{\log }_2\frac{|C_k|}{|D|}$$

2. 计算特征 $A$ 对于训练集 $D$ 的经验条件熵 $H(D|A)$ ：

$$H(D|A)=\sum _{i=1}^n\frac{|D_i|}{|D|}H(D_i)=-\sum _{i=1}^n\frac{|D_i|}{|D|}\sum _{k=1}^K\frac{|D_{ik}|}{|D_i|}\log \frac{|D_{ik}|}{|D_i|}$$

3. 计算信息增益：

$$g(D,A)=H(D)-H(D|A)$$

信息增益比：定义为信息增益 $g(D,A)$ 与训练数据集 $D$ 关于特征 $A$ 的值的熵 $H_A(D)$ 之比，即：
$$g_R(D,A)=\frac{g(D,A)}{H_A(D)}$$
其中：
$$H_A(D)=-\sum _{i=1}^n\frac{|D_i|}{|D|}{\log }_2\frac{|D_i|}{|D|}$$
以信息增益作为划分训练集的特征，会存在一个问题：偏向于选择取值较多的特征，因为这样算出来的 $H(D|A)$ 往往更小。所以可以使用信息增益比进行矫正。

决策树的生成

ID3 算法

输入：训练集 $D$ ，特征集 $A$ 和阈值 $\epsilon$ ；

输出：决策树 $T$ ；

1. 若 $D$ 中所有实例属于同一类 $C_k$ ，则 $T$ 为单节点数，并将类 $C_k$ 作为该节点的类标记，返回 $T$ ;
2. 若 $A=\varnothing$ ，则 $T$ 为单节点树，并将 $D$ 中实例数最多的类 $C_k$ 作为该节点的类标记，返回 $T$ ；
3. 否则，计算 $A$ 中各特征对 $D$ 的信息增益最大的特征 $A_g$ ：
   1. 若 $g(D,A_g)<\epsilon$ ，则不再分支，将 $T$ 置为单节点树，并将 $D$ 中实例数最多的类 $C_k$ 作为该节点的类标记，返回 $T$ ；
   2. 否则，依据 $A_g$ 的各个取值，将 $D$ 分割为若干子集 $D_i$ （丢弃非空子集），递归地以 A − { A g } A-\set{A_g} A−{Ag​} 为特征集构建子节点；

C4.5 的生成算法

与 ID3 基本类似，但是使用信息增益比来选择 $A_g$ ；

决策树的剪枝

为了提高模型的泛化能力，我们需要对生成的决策树进行剪枝。剪枝往往通过极小化决策树整体的损失函数来实现，这里介绍一个简单的剪枝算法。

损失函数：设 $T$ 的叶子节点个数为 $|T|$，第 $t$ 个叶子节点的样本数为 $N_t$ ，该叶子节点中属于类别 $C_k$ 的样本数为 $N_{tk}$ 。$H_t(T)$ 为节点 $t$ 上的经验熵，$\alpha \ge 0$ 为参数。则决策树学习的损失函数可以定义为：
$$C_{\alpha }(T)=\sum _{t=1}^{|T|}{N}_t{H}_t(T)+\alpha |T|$$

其中经验熵为：
$$H_t(T)=-\sum _k\frac{|N_{tk}|}{|N_t|}\log \frac{|N_{tk}|}{|N_t|}$$
则右边第一项展开为：
$$C(T)=\sum _{t=1}^{|T|}{N}_t{H}_t(T)=-\sum _{t=1}^{|T|}\sum _{k=1}^K{N}_{tk}\log \frac{N_{tk}}{N_t}$$
此时：
$$C_{\alpha }(T)=C(T)+\alpha |T|$$
$\alpha$ 类似于正则化系数。

树的剪枝算法：目标为最小化损失函数

• 输入：生成算法产生的整个树 $T$ ，参数 $\alpha$ ；
• 输出：修建后的子树 $T_{\alpha }$ ；

1. 计算每个节点的经验熵；（对于内部节点，则以它所有后续节点的所有样本实例来计算经验熵）
2. 递归地从树的叶节点向上回缩：设对于某一个叶子节点的父节点，将其子节点回缩；回缩之前与之整体树分别为 $T_B$ 与 $T_A$ ，若：

$$C_{\alpha }(T_A)\le C_{\alpha }(T_B)$$

则进行剪枝；

3. 重复，直到无法继续减少损失函数为止；

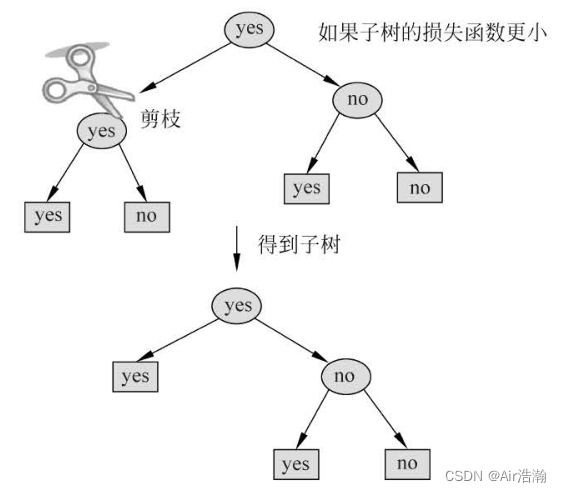
注意：

• 由于损失函数使用的是叶子节点的个数 $|T|$ ，因此损失函数的计算可以在局部进行；
• 对于二叉决策树而言，每剪枝一次，叶子节点就减少一个（因为原来的父节点变成了叶子节点），此时 $\alpha$ 就代表判断是否剪枝的阈值。若增加的经验熵大于 $\alpha$ ，则不进行剪枝。$\alpha$ 越大，则树越小；$\alpha$ 越小，则树越大；

CART 算法

CART 全称为分类与回归树（classification and regression tree），由特征选择、树的生成及剪枝组成。CART 假设决策树为二叉树，内部节点的特征取值为 ”是“ 或 ”否“。

CART 回归树的生成

回归树的生成思路：此时输出变量 $Y$ 是连续变量，而输入变量 $X$ 的各个维度往往也是连续变量。可以把回归树想象成对输入空间（特征空间）不断划分，假设已经划分为 $M$ 个单元 $R_1,R_2,\cdots ,R_M$ （其实就是对应 $M$ 个叶子节点） ，并且每一个划分单元 $R_m$ 上有一个固定的输出值 $c_m$ 。则对于某一实例 $x$ ，其所属的划分单元的输出值就是回归树的预测值，表示为：
$$f(x)=\sum _{m=1}^M{c}_{m}I(x\in R_m)$$
在某一个划分单元内，我们使用平方误差 $L(R_m)=\sum _{x_i\in R_m}(y_i-f(x_i){)}^2$ 作为损失函数，已知此时输出值 $c_m$ 的最优值为划分单元内每个实例对应输出值的平均值：
$${\hat{c}}_m=\frac{1}{|R_m|}\sum _{x_i\in R_m}{y}_i$$
对于如何划分，采用启发式的方法。选择第 $j$ 个变量 $x^{(j)}$ （即第 $j$ 个特征）和某个取值 $s$ ，作为切分变量和切分点，并定义两个区域：
R 1 ( j , s ) = { x ∣ x ( j ) ≤ s } 和 R 2 ( j , s ) = { x ∣ x ( j ) > s } R_1(j,\,s)=\set{x|x^{(j)}\leq s} \quad\text{和}\quad R_2(j,\,s)=\set{x|x^{(j)}\gt s} R1​(j,s)={x∣x(j)≤s}和R2​(j,s)={x∣x(j)>s}
我们的目标是选择最优切分变量 $j$ 和最优切分点 $s$ ，即求解：
$$\underset{j,s}{\min }\left[\underset{c_1}{\min }\sum _{x_i\in R_1(j,s)}(y_i-c_1{)}^2+\underset{c_2}{\min }\sum _{x_i\in R_2(j,s)}(y_i-c_2{)}^2\right]$$
显然 $c_1$ 和 $c_2$ 的选择也是区域内的平均值；我们遍历每个 $j$ ，找到最优切分点 $s_j$ ，选出所有切分变量中平方误差最小的一个 $(j,s_j)$ 。这样的回归树通常称为 最小二乘回归树。

最小二乘回归树生成算法：

• 输入：训练集 $D$ ，停止计算的条件；
• 输出：回归树 $f(x)$ ；

1. 选择最优切分变量 $j$ 与切分点 $s$ ，求解：

$$\underset{j,s}{\min }\left[\underset{c_1}{\min }\sum _{x_i\in R_1(j,s)}(y_i-c_1{)}^2+\underset{c_2}{\min }\sum _{x_i\in R_2(j,s)}(y_i-c_2{)}^2\right]$$

2. 用选定的对 $(j,s)$ 划分区域并决定相应的输出值：

R 1 ( j , s ) = { x ∣ x ( j ) ≤ s } , R 2 ( j , s ) = { x ∣ x ( j ) > s } c ^ m = 1 ∣ R m ∣ ∑ x i ∈ R m ( j , s ) y i , x ∈ R m , m = 1 , 2 \begin{aligned} R_1(j,\,s)=\set{x|x^{(j)}\leq s},\quad R_2(j,\,s)=\set{x|x^{(j)}\gt s} \\ \hat c_m=\frac{1}{|R_m|}\sum\limits_{x_i\in R_m(j,s)}y_i,\quad x\in R_m,\quad m=1,2 \end{aligned} R1​(j,s)={x∣x(j)≤s},R2​(j,s)={x∣x(j)>s}c^m​=∣Rm​∣1​xi​∈Rm​(j,s)∑​yi​,x∈Rm​,m=1,2​

3. 递归对两个子区域生成决策树，直到满足停止条件：达到最小样本数、最大深度、最小损失减少、没有特征等；
4. 将输入空间划分为 $M$ 个单元 $R_1,R_2,\cdots ,R_M$ ，得到决策树：

$$f(x)=\sum _{m=1}^M{c}_{m}I(x\in R_m)$$

CART 分类树的生成

基尼指数：也成为基尼不纯度，分类问题中，假设有 $K$ 个类，样本属于第 $k$ 类的概率为 $p_k$ ，则概率分布的基尼指数定义为：
$$\text{Gini}(p)=\sum _{k=1}^K{p}_k(1-p_k)=1-\sum _{k=1}^K{p}_k^2$$
基尼指数可以理解为，从样本集中随机选取两个样本，其不属于同一类的概率。

给定样本集合 $D$ ，其基尼指数（应该叫经验基尼指数？）为：
$$\text{Gini}(D)=1-\sum _{k=1}^K{\left(\frac{|C_k|}{|D|}\right)}^2$$
在特征 $A$ 和其某一划分条件的条件下，集合 $D$ 的基尼指数（应该叫经验条件基尼指数？）为：
$$\text{Gini}(D,A)=\frac{|D_1|}{|D|}\text{Gini}(D_1)+\frac{|D_2|}{|D|}\text{Gini}(D_2)$$
在二分类问题中，基尼指数、熵（以 2 为底）的一半 $\frac{H(p)}{2}$ 和分类误差率的关系为：

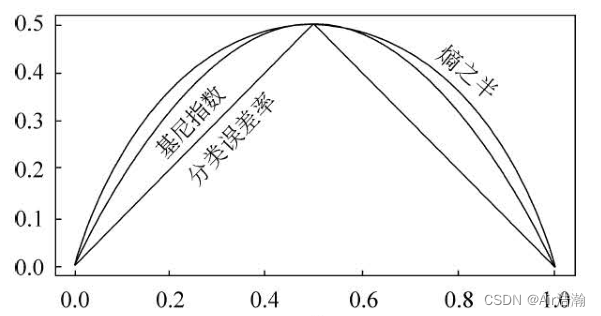
CART 分类树使用基尼指数选择最优特征：

• 基尼指数计算更快，不涉及对数计算；
• 熵对于不平衡程度更敏感，分布相对平衡的数据集使用熵会更合适；

CART分类树生成算法：

• 输入：训练集 $D$ ，停止计算的条件；
• 输出：决策树 $f(x)$ ；

1. 遍历每个特征 $A$ 和可能的取值 $a$ ，以 $A=a$ 作为划分条件计算划分后的基尼指数。选择得到最小的基尼指数的 $(A,a)$ 作为最优特征和最优切分点；
2. 依据 $(A,a)$ 将 $D$ 划分为两个子集，并对两个子集递归划分，直到满足停止条件；
3. 叶子节点中，使用多数表决法决定其类，生成 CART 决策树；

注意：CART 树生成过程中，一般来说某个特征被某个节点使用过后，该节点的后续节点的划分将不再使用该特征，这个特性有助于确保决策树的多样性和不过度拟合。但并不是说一个特征只能使用一次，而是一条从上到下的路径只能出现一次。但是该做法可能导致某些情况下的不充分利用特征。

CART 剪枝

CART 剪枝算法包含两个步骤：

• 从”完全生长“的决策树 $T_0$ 的底端开始不断剪枝，直到根节点，一次得到一个子树序列 { T 0 , T 1 , ⋯ , T n } \set{T_0,T_1,\cdots,T_n} {T0​,T1​,⋯,Tn​} ；
• 在独立的验证集上交叉验证子树序列，从中选择最优子树；

剪枝过程：定义损失函数为（$C(T)$ 可以是基尼指数）：
$$C_{\alpha }(T)=C(T)+\alpha |T|$$
前面说过，$\alpha$ 类似于一个阈值，控制着决策树的剪枝程度。我们可以采用递归的方法对树进行剪枝，将 $\alpha$ 逐渐增大，得到一系列子树 { T 0 , T 1 , ⋯ , T n } \set{T_0,T_1,\cdots,T_n} {T0​,T1​,⋯,Tn​} 。

对于 $T_0$ 的某个内部节点 $t$ ，以 $t$ 为单节点树的损失函数为：
$$C_{\alpha }(t)=C(t)+\alpha$$
以 $t$ 为根节点的子树 $T_t$ 的损失函数为：
$$C_{\alpha }(T_t)=C(T_t)+\alpha |T_t|$$
$\alpha$ 大时，选择 $t$ 较好（损失更小）；$\alpha$ 小时，选择保留 $T_t$ 较好；阈值为：
$$\alpha =\frac{C(t)-C(T_t)}{|T_t|-1}$$
CART 剪枝算法 ：

• 输入：CART 算法生成的决策树 $T_0$ ；
• 输出：最优决策树 $T_{\alpha }$ ；

1. 初始化 $k=0$ ，当前树为 $T=T_0$；

2. 令 $\alpha =+\infty$；

3. 自下而上地对各个内部节点 $t$ 计算：

$$g(t)=\frac{C(t)-C(T_t)}{|T_t|-1},\alpha =\min (\alpha ,g(t))$$

4. 对于 $g(t)=\alpha$ 的内部节点 $t$ 进行剪枝，得到新的树 $T$ ；

5. 更新 $k=k+1$ ，记录 $T_k=T$ ，${\alpha }_k=\alpha$ ；（注意这里更新完 $k$ 以后才记录）

6. 若 $T_k$ 不是根节点或者只有两个子节点，则回到步骤 2，否则停止算法；

7. 采用交叉验证法从 { T 0 , T 1 , ⋯ , T n } \set{T_0,T_1,\cdots,T_n} {T0​,T1​,⋯,Tn​} 中选取最优子树 $T_{\alpha }$ ；

注意：每次都选择最小的 $\alpha$ ，相当于尽可能保留树的节点，所以 { T 0 , T 1 , ⋯ , T n } \set{T_0,T_1,\cdots,T_n} {T0​,T1​,⋯,Tn​} 集合中树是逐渐变小的，${\alpha }_k$ 是逐渐变大的；

我有一个问题，某个内部节点的 $\alpha$ 有没有可能比其后续节点的 $\alpha$ 要小？就是有没有可能出现先剪了父节点，后剪了子节点的情况？

我们考虑某一个内部节点 $t$，其对应的数据集为 $D$ ；它的两个子节点 $t_1$ 和 $t_2$ 将数据集分为 $D_1$ 和 $D_2$ 两部分，则：
$$\begin{array}{rl}g(t)=& \frac{C(t)-C(T_t)}{|T_t|-1}\\ =& \frac{\left(1-\sum _{k=1}^K{\left(\frac{C_k}{D}\right)}^2\right)-\frac{D_1}{D}\left(1-\sum _{k=1}^K{\left(\frac{C_{k1}}{D_1}\right)}^2\right)-\frac{D_2}{D}\left(1-\sum _{k=1}^K{\left(\frac{C_{k2}}{D_2}\right)}^2\right)}{|T_t|-1}\\ =& \frac{\frac{D_1}{D}\sum _{k=1}^K{\left(\frac{C_{k1}}{D_1}\right)}^2+\frac{D_2}{D}\sum _{k=1}^K{\left(\frac{C_{k2}}{D_2}\right)}^2-\sum _{k=1}^K{\left(\frac{C_k}{D}\right)}^2}{|T_t|-1}\end{array}$$
这个值跟好多因素有关。。。感觉没法确定；但我认为父节点的 $\alpha$ 应当是更大的。