Bayes决策：身高与体重特征进行性别分类

代码与文件请从这里下载：Auorui/Pattern-recognition-programming: 模式识别编程 (github.com)

简述

分别依照身高、体重数据作为特征，在正态分布假设下利用最大似然法估计分布密度参数，建立最小错误率Bayes分类器，写出得到的决策规则，将该分类器应用到测试样本，考察测试错误情况。在分类器设计时考察采用不同先验概率（如0.5对0.5, 0.75对0.25, 0.9对0.1等）进行实验，考察对决策规则和错误率的影响。

同时采用身高与体重数据作为特征，在正态分布假设下估计概率密度，建立最小错误率Bayes分类器，写出得到的决策规则，将该分类器应用到训练/测试样本，考察训练/测试错误情况。比较相关假设和不相关假设下结果的差异。在分类器设计时可以考察采用不同先验概率进行实验，考察对决策和错误率的影响。

最小错误率贝叶斯决策

这里要对男性和女性的数据进行分类，先要求解先验概念P(x)，这个概率是通过统计得到的，或者依据自身依据经验给出的一个概率值，所以这个值是可以进行设定的，可选择0.5对0.5，0.75对0.25，0.9对0.1这些进行测试。

在贝叶斯统计中，后验概率是在考虑新信息之后事件发生的修正或更新概率。后验概率通过使用贝叶斯定理更新先验概率来计算。

$P(w_{i}|x)=\frac{p(x|w_{i})\times P(w_{i})}{p(x)}$

其中 $p(x)$ 为x的概率密度函数，即是：

$p(x)=\sum_{i=1}^{2}p(x|w_{i})p(w_{i})$

贝叶斯决策可以使用下面的等式来等价表示为

$p(x|w_{1})P(w_{1})>p(x|w_{2})P(w_{2})$

如果满足上式条件，则x属于 $w_{1}$ ，否则就属于 $w_{2}$ ，这个就是最小错误贝叶斯决策规则。

最小风险贝叶斯决策

在实际的应用中，分类错误率最小并不一定是最好的标准，不同类别的分类错误可能会导致不同的后果。有时，某些类别的错误分类可能比其他类别更为严重。例如，在医疗诊断中，将疾病误诊为健康可能比将健康误诊为疾病更为严重。在有决策风险时候，根据风险重新选择区域 $R_{1}$ 和 $R_{2}$ 从而使得 $P_{e}$ 最小。与 $w_{k}$ 相关的风险或损失定义为:

$r_{k}=\sum_{i=1}^{c}\lambda _{ki}\int_{R_{i}}p(x|w_{k})dx$

对于本数据，只有两类：

$l_{1}=\lambda _{11}p(x|w_{1})p(w_{1})+\lambda _{21}p(x|w_{2})p(w_{2})$

$l_{2}=\lambda _{12}p(x|w_{1})p(w_{1})+\lambda _{22}p(x|w_{2})p(w_{2})$

若 $l_{1}<l_{2}$ ，则 $x$ 属于 $w_{i}$ 类，即有

$(\lambda _{12}-\lambda _{11})p(x|w_{1})P(w_{1})>(\lambda _{21}-\lambda _{22})p(x|w_{2})P(w_{2})$

再经过简化，当 $w_{2}$ 类的样本被错误的分类会产生更严重的后果，可设置为 $\lambda _{21}>\lambda _{12}$ ，所以若 $p(x|w_{2})>p(x|w_{1})\frac{\lambda _{12}}{\lambda _{21}}$ ，则判定为 $w_{2}$ 类。

数据预处理

首先我们可以观察我们的数据：

它大概是这样分布的，一行数据为身高和体重。你可以使用python文件按行读取进行数据清洗，这里可以直接使用np.loadtxt，它会返回一个二维的数组，使用切片的方法就能划分出身高和体重的特征并进行均值方差化。

# @Auorui
import numpy as np
from scipy.stats import normclass Datasets:# 一个简单的数据加载器def __init__(self, datapath, t):self.datapath = datapathself.data = np.loadtxt(self.datapath)  # 二维数组self.height = self.data[:, 0]self.weight = self.data[:, 1]self.length = len(self.data)self.t = tdef __len__(self):return self.lengthdef mean(self, data):# 均值,可以使用np.mean替换total = 0for x in data:total += xreturn total / self.lengthdef var(self, data):# 方差,可以使用np.var替换mean = self.mean(data)sq_diff_sum = 0for x in data:diff = x - meansq_diff_sum += diff ** 2return sq_diff_sum / self.lengthdef retain(self, *args):# 保留小数点后几位formatted_args = [round(arg, self.t) for arg in args]return tuple(formatted_args)def __call__(self):mean_height = self.mean(self.height)var_height = self.var(self.height)mean_weight = self.mean(self.weight)var_weight = self.var(self.weight)return self.retain(mean_height, var_height, mean_weight, var_weight)

数据加载

def Dataloader(maledata,femaledata):mmh, mvh, mmw, mvw = maledata()fmh, fvh, fmw, fvw = femaledata()male_height_dist = norm(loc=mmh, scale=mvh**0.5)male_weight_dist = norm(loc=mmw, scale=mvw**0.5)female_height_dist = norm(loc=fmh, scale=fvh**0.5)female_weight_dist = norm(loc=fmw, scale=fvw**0.5)data_dist = {'mh': male_height_dist,'mw': male_weight_dist,'fh': female_height_dist,'fw': female_weight_dist}return data_dist

这里使用字典的方式存储男女数据的正态分布化。

计算概率密度函数（pdf值）以及贝叶斯决策

这里我们将会采用身高进行最小风险贝叶斯决策，采用体重进行最小错误率贝叶斯决策，采用身高、体重进行最小错误率贝叶斯决策。

def classify(height=None, weight=None, ways=1):"""根据身高、体重或身高与体重的方式对性别进行分类:param height: 身高:param weight: 体重:param ways: 1 - 采用身高2 - 采用体重3 - 采用身高与体重:return: 'Male' 或 'Female'，表示分类结果"""# 先验概率的公式 : P(w1) = m1 / m ,样本总数为m,属于w1类别的有m1个样本。p_male = 0.5p_female = 1 - p_malecost_male = 0  # 预测男性性别的成本,设为0就是不考虑了cost_female = 0  # 预测女性性别的成本cost_false_negative = 10  # 实际为男性但预测为女性的成本cost_false_positive = 5  # 实际为女性但预测为男性的成本assert ways in [1, 2, 3], "Invalid value for 'ways'. Use 1, 2, or 3."assert p_male + p_female == 1., "Invalid prior probability, the sum of categories must be 1"# if ways == 1:#     assert height is not None, "If mode 1 is selected, the height parameter cannot be set to None"#     p_height_given_male = male_height_dist.pdf(height)#     p_height_given_female = female_height_dist.pdf(height)###     return 1 if p_height_given_male * p_male > p_height_given_female * p_female else 2if ways == 1:assert height is not None, "If mode 1 is selected, the height parameter cannot be set to None"p_height_given_male = male_height_dist.pdf(height)p_height_given_female = female_height_dist.pdf(height)risk_male = cost_male + cost_false_negative if p_height_given_male * p_male <= p_height_given_female * p_female else cost_femalerisk_female = cost_female + cost_false_positive if p_height_given_male * p_male >= p_height_given_female * p_female else cost_malereturn 1 if risk_male <= risk_female else 2if ways == 2:assert height is not None, "If mode 2 is selected, the weight parameter cannot be set to None"p_weight_given_male = male_weight_dist.pdf(weight)p_weight_given_female = female_weight_dist.pdf(weight)return 1 if p_weight_given_male * p_male > p_weight_given_female * p_female else 2if ways == 3:assert height is not None, "If mode 3 is selected, the height and weight parameters cannot be set to None"p_height_given_male = male_height_dist.pdf(height)p_height_given_female = female_height_dist.pdf(height)p_weight_given_male = male_weight_dist.pdf(weight)p_weight_given_female = female_weight_dist.pdf(weight)return 1 if p_height_given_male * p_weight_given_male * p_male > p_height_given_female * p_weight_given_female * p_female else 2return 3

使用测试集验证并计算预测准确率

def test(test_path,ways=3):test_data = np.loadtxt(test_path)true_gender_label=[]pred_gender_label=[]for data in test_data:height, weight, gender = datatrue_gender_label.append(int(gender))pred_gender = classify(height, weight, ways)pred_gender_label.append(pred_gender)if pred_gender == 1:print('Male')elif pred_gender == 2:print('Female')else:print('Unknown\t')return true_gender_label, pred_gender_labeldef accuracy(true_labels, predicted_labels):assert len(true_labels) == len(predicted_labels), "Input lists must have the same length"correct_predictions = sum(1 for true, pred in zip(true_labels, predicted_labels) if true == pred)total_predictions = len(true_labels)accuracy = correct_predictions / total_predictionsreturn accuracy

预测结果

采用身高进行最小风险贝叶斯决策

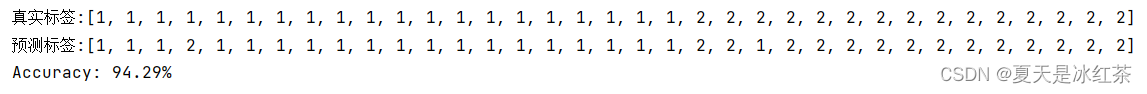
当采用身高进行最小风险贝叶斯决策，准确率在test1数据上的准确率为94.29%，在test2数据上的准确率为91.0%。

采用体重进行最小错误率贝叶斯决策

当采用体重进行最小风险贝叶斯决策，准确率在test1数据上的准确率为94.29%，在test2数据上的准确率为85.33%。

采用身高、体重进行最小错误率贝叶斯决策

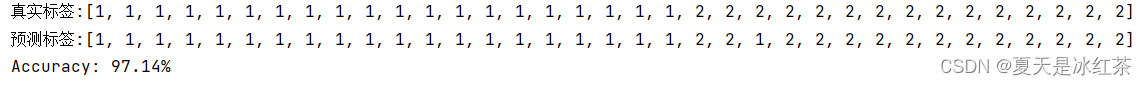
当采用身高、体重进行最小错误率贝叶斯决策，准确率在test1数据上的准确率为97.14%，在test2数据上的准确率为90.33%。

添加新的特征

除了身高、体重的组合，我们也可以延伸出新的特征，比如bmi。

def calculate_bmi(height,weight):# 计算BMI作为新特征height_meters = height / 100  # 将身高从厘米转换为米bmi = weight / (height_meters ** 2)  # BMI计算公式return bmi

这样能做出的特征就更多了，感兴趣的不妨沿着这个思路继续做。