学习目的

SPSS第三讲 | 正态分布怎么检验？看这篇文章就够了

软件版本

IBM SPSS Statistics 26。

原始文档

《小白爱上SPSS》课程
#统计原理

为什么要假设它服从正态分布呢?

一方面，是由于正态分布非常普通平凡，所以假设一个随机事件服从正态分布，比假设其他分布的成功率更高。
另一方面，是因为正态分布能够指明探索的方向。比如，如果我们验证后发现，这个随机事件不服从正态分布，那它就一定不满足正态分布背后的中心极限定理。而不满足中心极限定理，我们就能知道——要么是它的影响因素不够多，要么是各种影响因素不相互独立，要么是某种影响因素的影响力太大等等…这时候，接下来的研究也就有了明确的方向。

t检验

正态分布是很多连续型数据比较分析的大前提，比如t检验、方差分析、相关分析以及线性回归等，均要求数据服从正态分布或近似正态分布。
但大多数人进行统计时容易忽略这一重要前提，导致统计效能下降和假阴性风险增加。
为此，在系统讲解推断性统计方法之前，本课程将呈现三种正态分布的检验方法，让我们一次性掌握正态分布的检验方法。

一、图形法

一提到正态分布，我们自然会想到一个钟型形状。如下图。特点是“中间多，两端少”。

那么，怎么检验一组数据是否服从正态分布呢？先呈现个案例。
案例：25名青少年数据如下表，请判断该组数据的身高是否服从正态？
导入数据，命令行：

GET FILE='E:\E盘备份\recent\小白爱上SPSS\小白数据\第三讲 正态分布.sav'. 

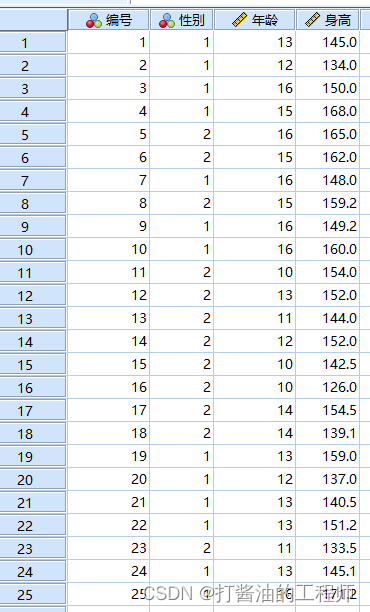
案例分析：身高数据明显属于连续型变量，可进行正态检验。

1、频数分布直方图

SPSS实战操作
第一步：【图形】→【旧对话框】→【直方图】
第二步：弹出直方图，将待分析变量移入【变量】框内，勾选显示正态曲线，本次我们考察“身高”数据，其他参数不用设置，直接【确定】命令执行。确定后，呈现如下直方图。

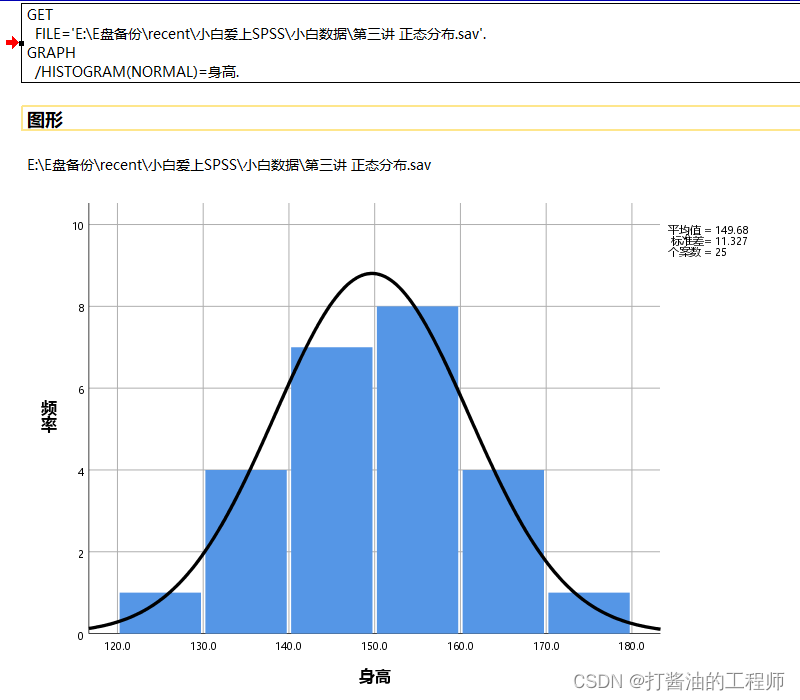
命令行：

GRAPH 			/*绘图*//HISTOGRAM(NORMAL)=身高.	/*直方图（正态）*/

解读

观察直方图的分布形状是否为一个倒扣“钟”型的对称形状，如果接近或相似，则可认为数据服从正态分布。
本例中，“身高”数据频数分布直方图的形状比较接近于倒扣的“钟形”，左右两边具有对称性，可认为该数据为正态分布数据。
执行：GRAPH /HISTOGRAM(NORMAL)=年龄. 显示“年龄”变量的直方图：

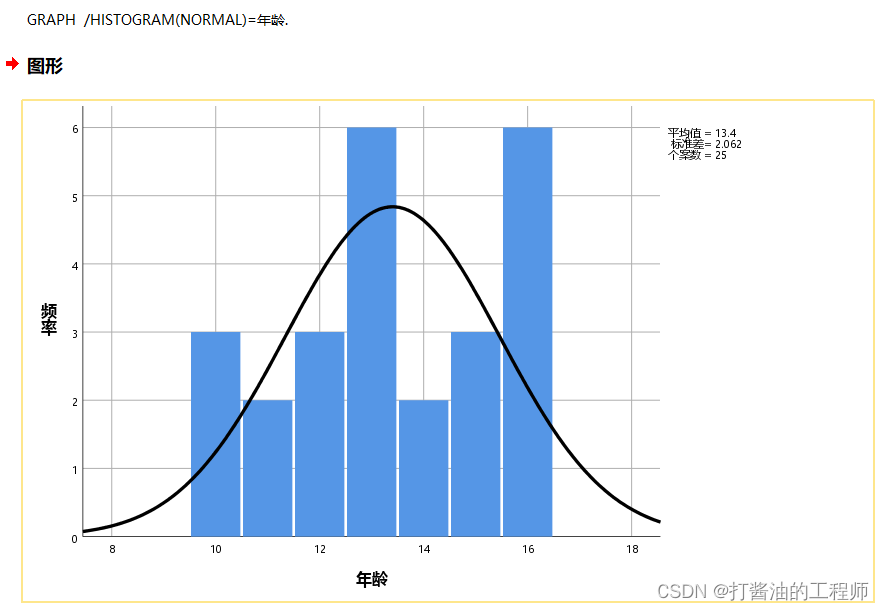
明显与正态曲线不重合。

2、正态Q-Q图

简介：Q-Q图反映了变量的实际分布与理论分布的符合程度，可以用来考察数据是否服从某种分布类型。若数据服从正态分布，则数据点应与理论直线基本重合。

操作

第一步：【分析】→【描述统计】→【QQ图】
第二步：将待分析的连续数据变量，如：身高，移入【变量】框内，软件默认是检验【正态分布】，其他参数不用设置，直接【确定】命令执行。

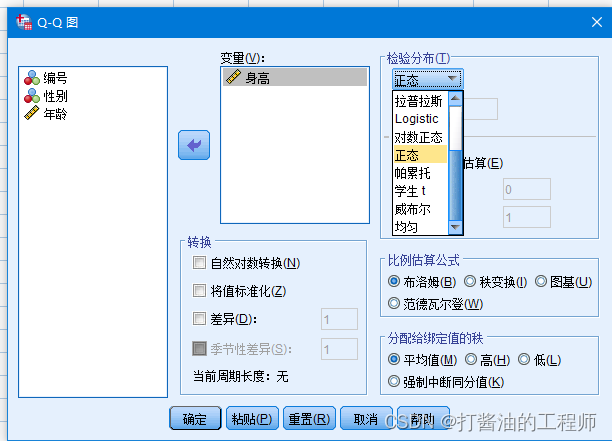
确定后，呈现如下Q-Q图。

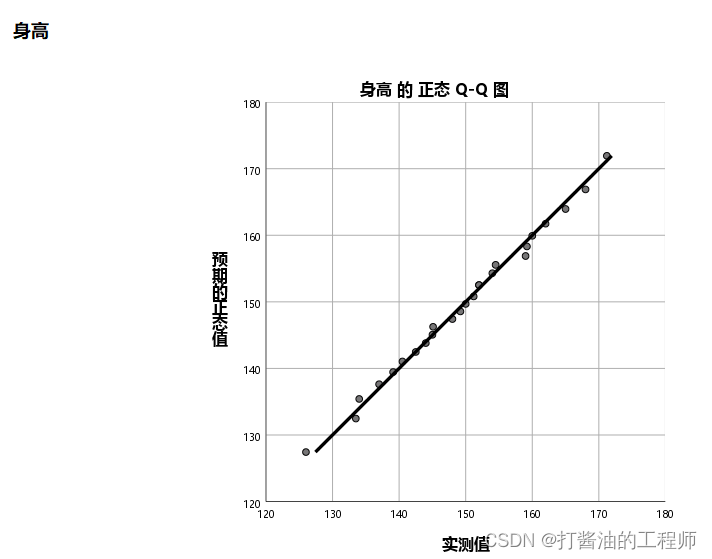
命令行：
···
PPLOT
/VARIABLES=身高 /核心变量，其他行为可选参数，有默认或初始值/
/NOLOG
/NOSTANDARDIZE
/TYPE=Q-Q
/FRACTION=BLOM
/TIES=MEAN
/DIST=NORMAL.
···

解读

观察Q-Q图上的点能否分布在一条直线上，分布在一条直线上则说明近似或服从正态分布。
本例中，身高绝大多数的点能分布在一条直线上，直线趋势明显，可认为该连续数据服从正态分布。

3、正态P-P图

简介：P-P图反映了变量的实际累积概率与理论累积概率的符合程度，可以用来考察数据是否服从某种分布类型。若数据服从正态分布，则数据点应与理论直线基本重合。与Q-Q图意义相似。

SPSS实战操作

第一步：【分析】→【描述统计】→【P-P图】
第二步：将待分析的连续数据变量移入【变量】框内，本例检测“身高”数据的正态分布，软件默认是检验【正态分布】，其他参数不用设置，直接【确定】命令执行。
命令行：
···
PPLOT
/VARIABLES=身高 /核心变量，其他行为可选参数，有默认或初始值/
/TYPE=P-P
/DIST=NORMAL.
···

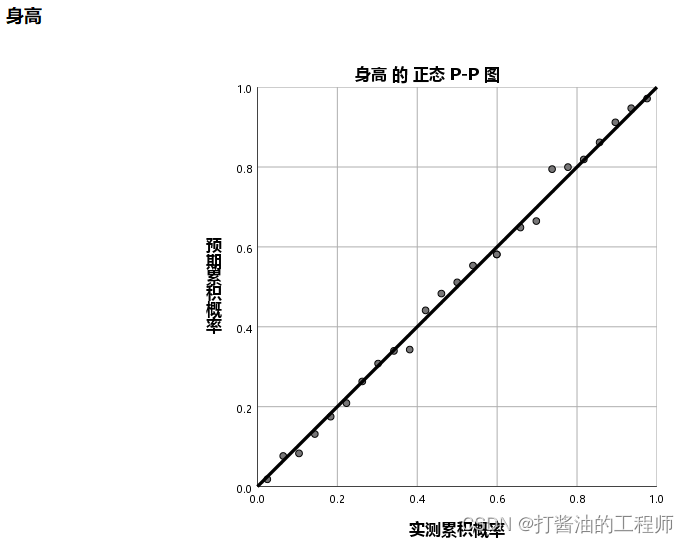
解读

观察P-P图上的点能否分布在理论分布的直线上，若基本分布在直线上则说明近似或服从正态分布。
本例中，“身高”的绝大多数的点能分布在一条直线上，直线趋势明显，可认为该连续数据服从正态分布。

二、偏度和峰度

简介：
[偏度]主要用于判定数据的对称性，整体数据偏左还是偏右，见下图。

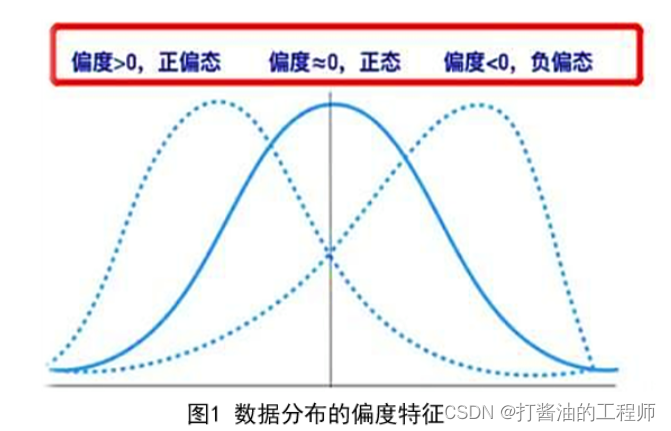
当偏度S≈0时，可认为分布是对称的，服从正态分布；
当偏度S>0时，分布为右偏，即拖尾在右边，峰尖在左边，也称为正偏态；
当偏度S<0时，分布为左偏，即拖尾在左边，峰尖在右边，也称为负偏态；
注意：数据分布的左偏或右偏，指的是数值拖尾的方向，而不是峰的位置。
[峰度]是用于判定数据分布的陡缓程度，见下图。

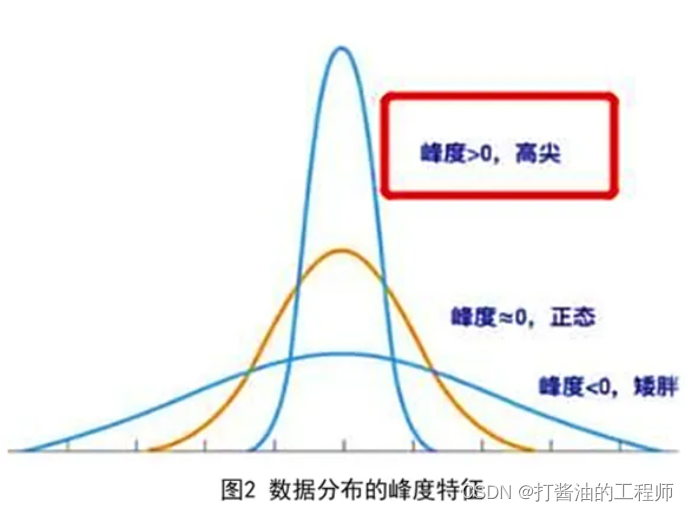
当峰度K≈0时，可认为分布的峰态合适，服从正态分布（不胖不瘦）；
当峰度K>0时，分布的峰态陡峭（高尖）；
当峰度K<0时，分布的峰态平缓（矮胖）；
了解偏度和峰度这两个统计量的含义很重要，是检验数据正态分布的重要指标。
实际上，我们收集到很难能满足S≈0，K≈0, 因此，可采用K与S系数来检验，检验公式如下。

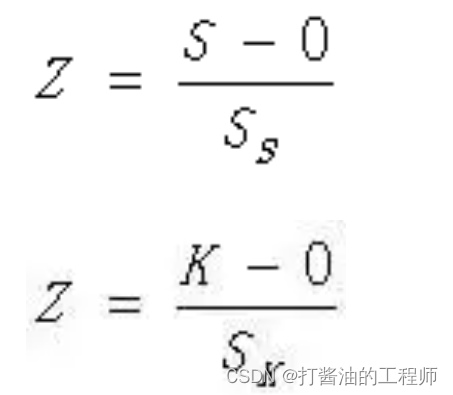
其中，SS和SK均为S系数和K系数的标准误。在α=0.05的情况下，Z值的绝对值大于1.96时，可认为K系数或S系数显著不等于0，即样本数据非正态。
SPSS实战操作
第一步：【分析】→【描述统计】→【描述】
第二步：将“身高”选入【变量】框中，点击【选项】，勾选“平均值”、“标准差”、“峰度”和“偏度”。

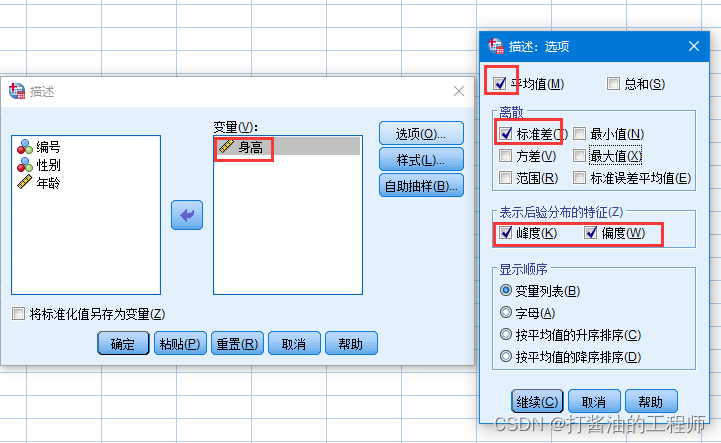
第三步：点击“继续”、“确定”，得到计算结果。
命令行：
···
DESCRIPTIVES VARIABLES=身高
/STATISTICS=MEAN STDDEV KURTOSIS SKEWNESS. /统计指标=平均值 标准差 峰度 偏度/
···

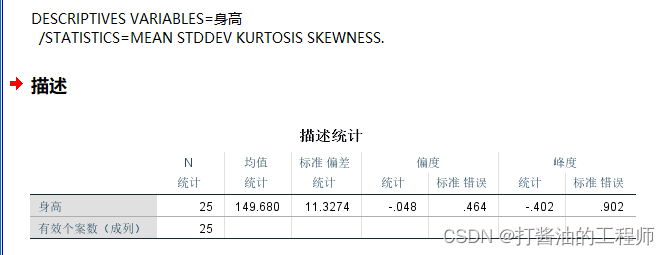
解读：

①计算偏度系数：
手算：

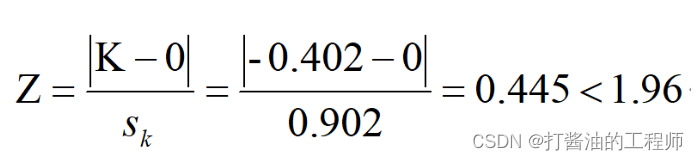
②计算峰度系数：
手算：

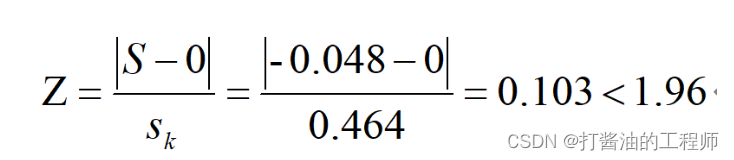
由以上结果可知，偏度系数和峰度系数的绝对值均小于1.96，可以认为该组样本数据符合正态分布。
需注意：当样本量过大（超过100）时，采用峰度和偏度系数会对正态性的情况有所偏误，此时，可以直接尝试采用图示法（直方图、P-P、Q-Q）的方法进行检验会更直观。

三、非参数检验法

简介：正态性检验属于非参数检验，原假设为“样本来自的总体与正态分布无显著性差异”，只有P>0.05才能接受原假设，即数据符合正态分布。
常见的正态性检验有Kolmogorov-Smirnov检验（即柯尔莫戈洛夫-斯米诺夫检验，简称K-S检验）和Shapiro-Wilk检验（即夏皮-威尔克检验，简称S-W检验），K-S检验适用于大样本数据，S-W检验适用于小样本数据，当检验结果的p值小于0.05，则认为数据不满足正态性。
SPSS实战操作
第一步：【分析】-【描述统计】-【探索】 打开探索对话框。
第二步：本例我们想分别检验男女两组的身高是否服从正态分布，故将身高选入【因变量】列表，将性别选入【因子列表】
点击 【图】 --勾选“直方图”“含检验的正态图”
点击【继续】–【确定】，得到探索性分析结果。输出结果有很多图表，我们只解释正态性检验结果。

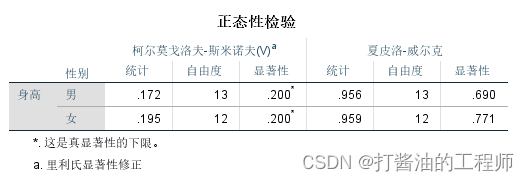
命令行：

EXAMINE VARIABLES=身高 BY 性别 /PLOT BOXPLOT NPPLOT /*若无此行，则不输出正态性检验表*//COMPARE GROUPS /STATISTICS DESCRIPTIVES /CINTERVAL 95 /MISSING LISTWISE /NOTOTAL.

结果解读：
当数据量≤50时，倾向于以夏皮洛-威尔克（S-W）检验结果为准；
当数据量>50时，倾向于以柯尔莫戈洛夫-斯米诺夫（K-S）检验结果为准；
当数据量>5000时，SPSS只会显示K-S检验结果。
本例中，我们比较25例男女中学生身高差异，需要分别看这两组的身高分布情况，上表显示，两组的样本量（可参考自由度那一列数值）均小于50，故以夏皮洛-威尔克（S-W）检验结果为准.
两组检验的p值（即显著性那一列）分别为0.690、0.771，均大于0.05，说明这两组身高均符合正态分布，故认为身高满足正态性。

注意事项

在使用S-W和K-S检验时需注意，当样本量较少的时候，检验结果不够敏感，即使数据分布有一定的偏离也不一定能检验出来；而当样本量较大的时候，检验结果又会太过敏感，只要数据稍微有一点偏离，P值就会<0.05，检验结果倾向于拒绝原假设，认为数据不服从正态分布。
所以，如果样本量足够多，即使检验结果P<0.05，数据来自的总体也可能是服从正态分布的。为此，我们要结合图直方图、P-P、Q-Q的图示法灵活使用。

四、规范表达

本次测量样本为25名，故采用夏皮洛-威尔克（S-W）检验，将SPSS输出结果整理为三线表，如下表1。
表1 身高的S-W正态性检验结果

从上表可知，男女生的正态性检验结果的统计分别为0.956和0.959，P值分别为0.690、0.771，均大于0.05。
同时结合直方图、P-P图和Q-Q图，可认为男生和女生的身高都服从正态分布。

五、小结

正态分布的检验方法包括图示法、偏度和峰度、非参数检验方法。
图形法检验正态分布往往是有效的，是实际应用中较为普遍的方式，是对正态分布显著性检验（如偏度和峰度的Z值、S-W及K-S检验）的有力辅助手段。
在实际的应用中，往往会出现明明直方图显示分布很对称，但参数检验的结果P值却<0.05，拒绝原假设认为不服从正态分布。
此时建议不要太刻意追求正态性检验的P值，一定要参考直方图、P-P图等图形工具来帮助判断。因此正态性检验三种方法均有重要实用意义。
很多统计学方法，如T检验、方差分析等，与其说要求数据严格服从正态分布，不如说“数据分布不要太偏态”更为合适。
小白学习完本节课内容之后，赶紧回去对40名大侠的数据进行正态性检验（第二讲数据），结果发现大侠们的身高、体重服从正态分布，而成绩不服从正态分布。
身高正态性检验（命令行）：

EXAMINE VARIABLES=身高/PLOT BOXPLOT NPPLOT /*若无此行，则不输出正态性检验表*//COMPARE GROUPS /STATISTICS DESCRIPTIVES /CINTERVAL 95 /MISSING LISTWISE /NOTOTAL.

身高检验结果：


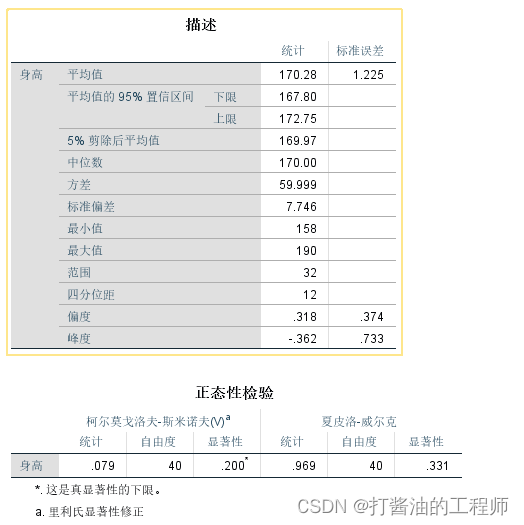
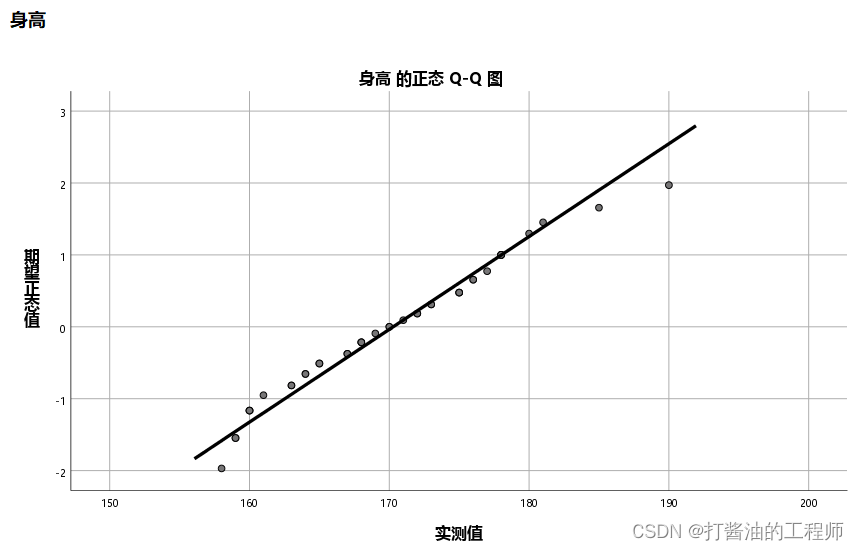
体重正态性检验（命令行）：

EXAMINE VARIABLES=体重/PLOT BOXPLOT NPPLOT /*若无此行，则不输出正态性检验表*//COMPARE GROUPS /STATISTICS DESCRIPTIVES /CINTERVAL 95 /MISSING LISTWISE /NOTOTAL.

体重检验结果：


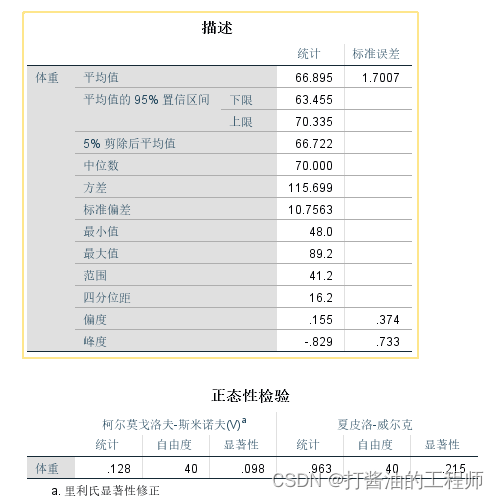
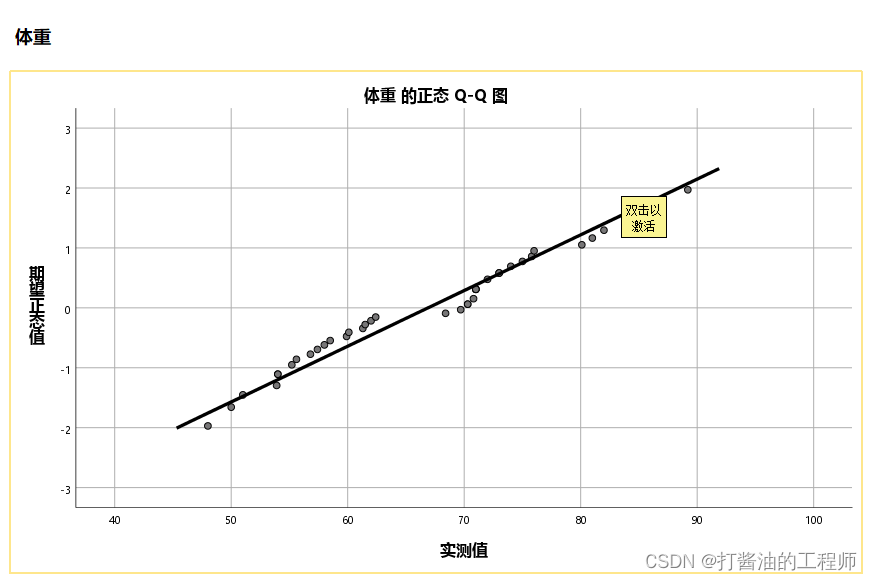
成绩正态性检验（命令行）：

EXAMINE VARIABLES=成绩/PLOT BOXPLOT NPPLOT /*若无此行，则不输出正态性检验表*//COMPARE GROUPS /STATISTICS DESCRIPTIVES /CINTERVAL 95 /MISSING LISTWISE /NOTOTAL.

成绩检验结果：

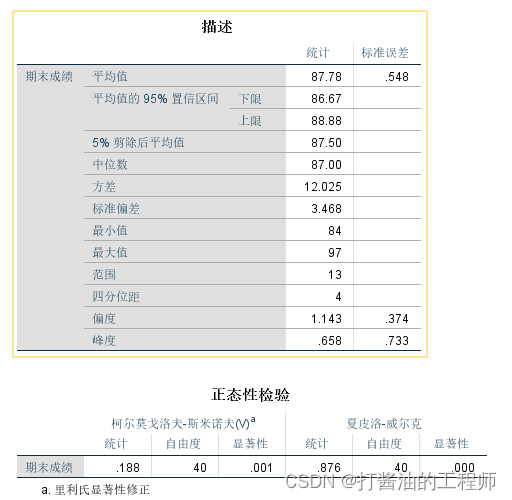
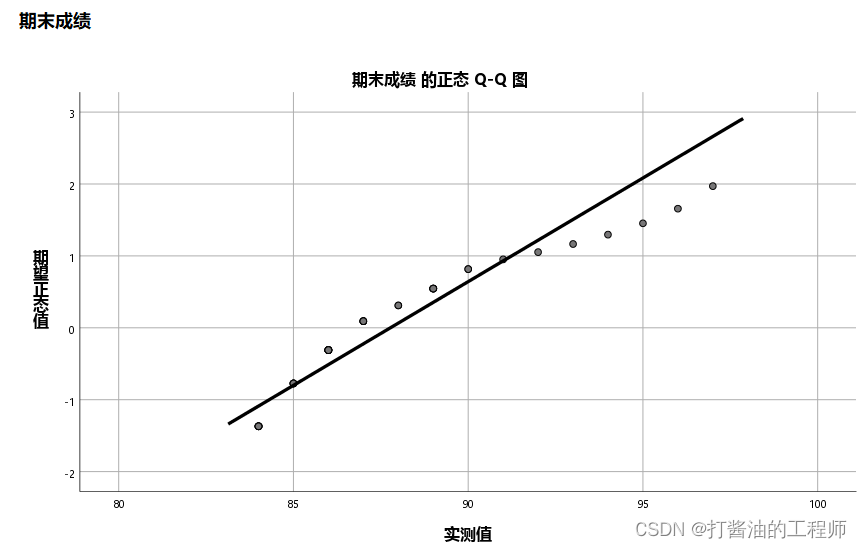
于是，大侠们的身高和体重采用平均数、标准差来描述，而成绩采用中位数和四分位距来描述。
小白把上次的描述性结果呈送给主任，主任看后，满意地点点头。
然后，转过头对小白说：“小白，我想了解下今年这些大侠们的体重是否超标了？如果超标，就要加强训练，减脂减重，你能比较出来吗？”
小白这时比较淡定了，因为他非常清楚，《小白爱上SPSS》课程下一讲，将开启假设检验，讲解差异比较的T检验。
所以，搬好小板凳，等待开课就好了！

划重点

1、正态分布的检验方法包括图示法、偏度和峰度、非参数检验方法。
2、实际应用不必太刻意追求偏峰度的Z值和S-W及K-S检验的P值，需要结合直方图、P-P图和Q-Q图来判断。
3、对于统计方法，与其说要求数据严格服从正态分布，不如说“数据分布不要太偏态”更为合适。