第 2 章 Fourier级数的基本属性(Basic Properties of Fourier Series)
Nearly fifty years had passed without any progress on
the question of analytic representation of an arbitrary
function, when an assertion of Fourier threw new light
on the subject. Thus a new era began for the de-
velopment of this part of Mathematics and this was
heralded in a stunning way by major developments in
mathematical Physics.
(将近五十年过去了,在任意函数的解析表示问题上没有取得任何进展,此时Fourier抛出的这个论断为这个主题的解决带来了新的曙光。因此,数学在这一领域的发展进入到了一个新的纪元,数学物理学的重大发展以惊人的方式预示了这一点。)
----------------------------------------------------------------- B. Riemann[rí:ma:n], 1854
在这一章,我们以严谨的 Fourier 级数研究开始。我们通过介绍主题中的主要对象来奠定基础,然后阐述我们之前已经触及的一些基本问题。
我们的第一个结果解决了唯一性问题:具有相同傅里叶系数的两个函数是否必然相等? 事实上,一个简单的论证表明,如果两个函数是连续的,那么实际上它们必须一致。
接下来,我们仔细看看Fourier[fúriə]级数的部分和。使用Fourier系数公式(涉及积分),我们发现这些总和可以方便地写成积分:
,
其中, 是一个函数族,,称为Dirichlet[di:rikléi]核(译注:“核”指核心,在整个公式中起着核心的控制作用)。 上面的表达式是函数 f 与
的卷积(convolution)。在我们的分析中,卷积将起着关键的作用。一般情况下,已知一族函数
。我们被导向分析当 n 趋近于无穷大时卷积
的属性。我们发现,假如函数 满足“好核(good kernels)”的3个重要属性,则以上卷积当n ->∞ 时趋近于 f(x)(至少,当f(x)是连续函数的时候)。在这种意义上,函数族
是恒等式的一个近似表达式。遗憾的是,Dirichlet核
并不属于好核这个类,这个事实表明,Fourier级数的收敛性是微秒的。
在这个阶段,我们不追求收敛性问题,而是考虑对函数的Fourier级数求和的各种其他方法。 第一种方法,涉及部分和的平均,这会导向具有好核的卷积,并产生一个重要的Fejér 定理。由此,我们推导出圆周上的连续函数可以用三角多项式一致逼近的事实。第二种方法,我们也可以对Abel意义上的Fourier级数求和,会再次遇到一族好核。在这种情况下,关于卷积和好核的结果导出了圆盘中稳态热传导方程Dirichlet问题的解,在上一章末尾考虑过。
1. 问题示例和公式化
我们从一个我们即将关注的这种函数的简短描述着手来探讨这个问题。因为函数 f 的Fourier系数定义为
,
其中,f 是一个闭区间[0,L]上的复值函数,在 f 上设置某些积分条件是必要的。因此,在本书的余下章节中,我们将假设所有的函数至少是Riemann[rí:ma:n]可积的(注:在初级阶段,我们限定在Riemann可积函数是很自然的。更高级的Lebesgue可积的概念将在本套书的第III册介绍)。有时候,将我们的注意力集中在更“规范(regular)”的函数上是只有启发性的,即,所谓“规范”的函数是指具有某种连续性和可微性属性的函数。下面,我们按照通用性递增的次序列出几种函数。我们强调一点,一般情况下,我们不会将我们的关注点仅限于实数函数,这与以下图片显示的可能相反(译注:下图可能仅显示实数的函数图);我们几乎总是允许函数在复数域 ℂ 上取值。且,有时候,我们会将函数看成是定义在圆周上而非一个区间上。我们下面的描述会基于这一原则。
A. 处处连续的函数。
在区间[0,L]上处处连续的复值函数 f 称为连续函数。 图1 (a)所示为典型的连续函数。在后面,我们将说明,圆周上的连续函数满足附加条件f (0) = f (L) 。
B. 分段(piecewise)连续的函数。
在区间[0,L]上仅存在有限多个不连续点的有界函数 f 称为分段连续函数。图1 (b)所示为具有简单不连续点的分段连续函数。
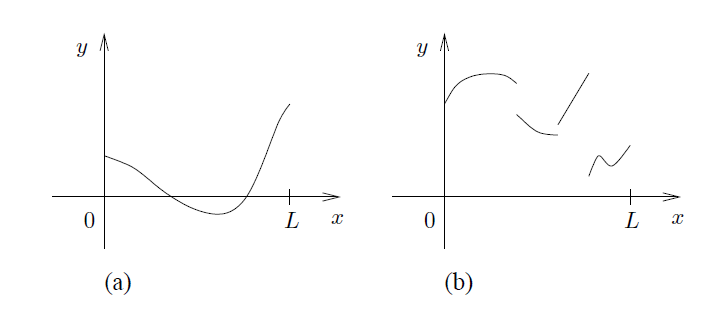
-----------------------------图1 在区间[0,L]上的连续函数和分段连续函数--------------------------------
这类函数的范围很广,足以说明接下来几章中的许多定理。 然而,为了逻辑完备性,我们还考虑了更一般的Riemann可积函数类。 这种更广泛的背景是自然的,因为Fourier系数的公式涉及积分。
C. Riemann可积函数。
这是我们即将关注的最通用的函数类。这类函数是有界的,但是,可能具有无限多个不连续点。我们回顾一下积分的定义。一个定义在闭区间[0,L]上的函数 f 是Riemann可积的,条件是,假如它有界,并且对于每一个ε > 0 (\mathcal{E}或ε),在闭区间[0,L]上都存在一个细分(N 等分) , 使得,只要 𝒰 (\mathcal{U})和 ℒ (\mathcal{L})分别是函数 f 对这个划分的上界和(译注:每个f(x)取这个区间上的最大值)与下界和(译注:每个f(x)取这个区间上的最小值),即
和
。
则我们有 𝒰 - ℒ < ε 。最后,我们说,对于一个复值函数,如果其实部和虚部分别是可积的,则我们就说这个复值函数是可积的。值得提醒的是,两个可积函数的和与积构成的函数也是可积的。
下面是在闭区[0,1]上具有无限多个不连续点的可积函数(译注:分段可积)的例子

其图形如下图 2 所示。注意,当 和
时,函数 f(x) 是不连续的。
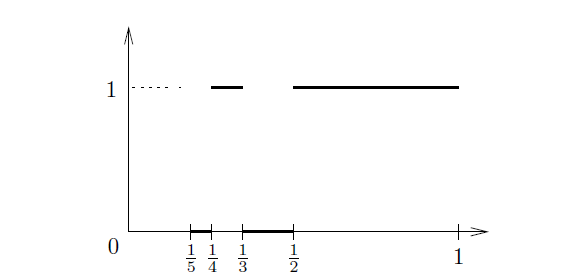
-----------------------------------------图2 一个Riemann可积函数-------------------------------------
更精选的在闭区间[0,1]上有稠密不不连续点的可积函数示例留在课后的问题1中描述。一般情况下,虽然可积函数可能有无穷多个不连续点,在确切的意义上讲,这些函数实际上的特征是,它们的不连续点并不多:即,它们是“微不足道的(negligible)”,即,可积函数不连续点的集合是“0测度的(measure 0)。” 在附录中,读者可以发现关于Riemann积分的更多详细信息。
在此以后,即使我们没有显式地指出我们所讨论的函数是可积的,我们都总是假设我们讨论的函数是可积的。
D. 圆周上的函数。
实数域 ℝ 上以 2π 为周期的周期函数(例如,指数函数 ) (译注:根据欧拉公式,
,在复平面上,单位圆指的就是复数
的轨迹,单位圆周上的函数坐标为x = cos(θ), y = i sin(θ)),以2π 为区间长度的函数和单位圆周上的函数之间存在着天然的联系(译注:自古以来,圆形一直是(现在仍然是)最简单的抽象理解形状。理解Fourier级数(因此还有Fourier变换,最后是离散Fourier变换)的关键,也是我们的一个最古老的愿望——用圆或最简单优雅的抽象人类构造来表达一切。用一句形象的话说,我们天生需要通过用圆圈来描述周围的世界从而理解它。)。这种联系产生如下。
单位圆周上的某点采用 的形式表示,其中 θ 是 2π 最小整数倍的这个条件下是唯一的。假如 F 是单位圆周上的一个函数,则我们可以针对每个θ 定义
,
并注意到,与此定义相关的是,f 是实数域 ℝ上以 2π 为周期的周期函数,即,对于所有的 θ,都有 f (θ + 2π) = f (θ)。函数 F 的可积性、连续性、和其它平滑性等属性取决于函数 f 的相应属性。例如,我们可以说,假如 f 在 2π长度的每一个区间上是可积的,则F 在圆周上是可积的。且,假如f 在实数域 ℝ上是连续的,则F 在圆周上是连续的,这与我们说成,f 在任意2π长度的区间上连续,这两者等效。再有,假如 f 具有一个连续的导数,则 F 连续可微,如此等等。
因为 f 具有 2π 周期,我们可以将其限定在任意 2π长度的区间上。比如说,限定在区间[0, 2π]或[-π, π]上,并且任何捕获单位圆周上的初始函数 F 。我们注意到,f一定取了区间端点的相同值,因为它们对应圆周上的同一点。反过来,区间[0, 2π ]上f(0) = f (2π) 的任何函数都可以延拓到实数域 ℝ上的周期函数,然后被视作等价于圆周上的函数。特别是,对于闭区间[0, 2π]上的连续函数f ,当且仅当f (0) = f (2π)时,其在圆周上产生一个连续函数。
总而言之,实数域 ℝ上以2π为周期的函数,和以长度2π为区间在其端点处取相同值的函数,这两者是同一数学对象的等价描述,即,都是圆周上的函数。
在这种联系中,我们涉及到一个项的记法的用法。当我们的函数定义在直线上的区间上时,我们使用x表示自变量(independent variable);当我们将这些函数看成是圆周上的函数时,我们通常将自变量x替换成θ。正如读者将会注意到的那样,我们不受此规则的严格约束,因为这种做法主要是为了方便。
1.1. 主要定义和一些示例
现在,我们以函数的Fourier级数的准确定义开始我们的Fourier分析的学习之旅。在此,确定(pin down)我们的函数的起始定义的位置很重要。假如 f 是一个定义在闭区间[a, b]上区间长度为L (即,b - a = L)的已知函数,则函数 f 的第n 项Fourier系数定义为
。
函数 f 的Fourier级数通常由
给出(注:在这一点上,我们不说任何关于级数收敛的事情。)。
有时候,我们将函数f 的Fourier系数写成 ,并使用下面的记法
来表示右侧的级数是函数 f 的Fourier级数(译注:因为角频率 ,
。)
例如,假如函数 f 是闭区间 [-π, π ]上的可积函数,则函数 f 的第 n 项Fourier系数是
,
以及函数 f 的Fourier级数是
。
在这儿,我们使用变量 θ,因为我们将它视作圆周上从-π到π的角度。
且,如果函数f 定义在闭区间[0, 2π]上,则这个公式与上面一样(除了在Fourier系数的定义时积分区间变成了[0, 2π])。
我们还可以考虑定义在圆周上的函数的Fourier系数和Fourier级数。按照我们前面的讨论,我们可以将一个圆周上的函数 f 看成是定义在实数据ℝ上的周期为 2π 的周期函数。我们可以将函数 f 限定在任意一个 2π 长度的区间上,例如,限定在[0, 2π]或[-π, π]上,然后再计算它的Fourier系数。幸运的是,f 是周期函数,其导致的积分取决于积分区间。因此,圆周上的函数的Fourier系数很好定义。
最后,有时候,我们会考虑给定的闭区间[0, 1]上的函数 g(x)。则
和
。
此处,我们使用了介于0到1之间的 x 作为变量。
当然,如果f 初始化到闭区间[0, 2π]上,则 g(x) = f(2πx) 定义在[0, 1],且变量的变化表明,f 的第n项Fourier系数等于g 的第n项Fourier系数。
Fourier级数是更大的称为三角级数(trigonometric series)的级数族中的一部分,根据定义,三角级数的表达式形式为 ,其中,
(译注:复数)。假如一个三角级数仅包括有限多项非零项,即,对于任意大的|n|,都有
,则称其为三角多项式(trigonometric polynomial);它的度(degree)是对所有
的|n|的最大值。
函数f 的Fourier级数的前N (N是一个正整数)部分和(partial sum)是三角多项式的一个特例,由
给出。
注意,根据定义,以上的和是对称的,因为n介于-N和N之间。因为Fourier级数分解为正弦级数和余弦级数,所以这是一种自然的选择。因此,Fourier级数的收敛(在本书中)将被理解为“极限”,因为 N 趋向于这些对称和的无穷大。
事实上,使用Fourier级数部分和,我们可以将第 1 章中提出的基本问题重新表述如下:
问题:在什么意义上, 随着
时收敛于 f 。
在进一步讨论这个问题之前,我们先来看一些简单的Fourier级数的例子。
例子1:令 。Fourier系数的积分要求使用简单的分部积分。首先,假如 n ≠ 0 ,则
(译注: , 令
,
, 根据分部积分公式,
, 则
)
,
假如 n = 0 ,很显然,我们有
,
因此,Fourier级数由
给出(译注:根据Euler公式
,因为
为偶函数,正好抵消掉。
第一个求和公式取所有非零整数(n≠0),第二个求和公式是Euler恒等式的应用(n ≥ 1)。可以用初等方法证明上述级数对每个 θ 收敛,但它收敛于 f(θ) 是不明显的。将在后面证明。
例子2:定义 。Fourier系数的积分要求使用简单的分部积分。首先,假如 n ≠ 0 ,则后续的积分按照前面例子使用的分部积分公式得到
。
例子3:闭区间 [0, 2π ] 上的函数
的 Fourier 级数是
,
其中,α 取值为任意非整数。
例子4:定义在x∈[-π,π]上的三角多项式
称为第 N 项Dirichlet核,在理论分析中具有根本性的重要性(我们后面将会看到)。注意,Fourier系数 具有属性:
。
Dirichlet核的一个封闭形式公式(a closed-form formula)(译注:闭公式,通用公式,标准公式等)是
。
这可以通过等比级数
和
的求和看出来。它们的和分别是
和
。
则它们的和为
,
给到了预期的结果。
例子5:通过绝对一致性收敛的级数定义的函数
。
称为泊松核(Poisson kernel)。
该函数隐含在第 1 章讨论的单位圆盘上稳态热传导方程的解中。注意,在计算 的Fourier系数的时候,我们可以交换积分与总和的次序,因为,对于每一个固定的r,总和按θ一致收敛,且可以获得第 n 项Fourier系数等于 r|n|
![]() 。读者也可以求对
。读者也可以求对 求级数和得到
。
事实上,
,
其中,两个级数都绝对收敛。第一个和(一个无穷等比级数)等于 ,第二个和等于
。将这两个级数相加,得到
,这正是前面
的级数和。Poisson核稍后将在函数的Fourier级数的Abel可和性的相关内容中再次出现。
让我们回到前面阐述的问题。函数 f 的Fourier级数的定义是纯形式化的,其是否收敛于 f 并不明显。事实上,要得出这个问题的解会很难,又或相对容易,这取决于在我们预期级数收敛的这种意义上,或者取决于我们施加于函数 f 上的限制条件。
我们说得更准确一些。为了讨论这个问题,我们假设函数 f (假设总是Riemann可积的)定义在闭区间[-π,π]上。读者可能要问的第一个问题便是,函数 f 的Fourier级数的部分和是否逐点地(pointwisely)收敛于f 。即。对于任意θ ,等式
(1)
是否都成立?
我们可以十分容易地看出,通常情况下,我们不能期这个等式对于任意θ都成立,因为,我们总是可以在某一点改变积分函数,而不用改变其Fourier系数。因此,假设函数f 是连续的周期函数,我们可以提出同样的疑问。长期以来,人们都认为在这些附加假设条件下,这个答案是“肯定的。” 当Du Bois-Reymond证明了存在连续函数,它的Fourier级数却在某一点发散,这让人感到惊呀。在下一章将给出这样的例子。尽管存在这种“负面”的结果,但是,我们也可以问,假如我们施加更多的平滑条件于 f 上,又会发生什么呢:例如,我们可以假设 f 是连续可微或者二次连续可微的。则,我们将会看到,f 的Fourier级数一致收敛于f 。
我们也可以通过在Cesµáro 或 Abel的意义上证明f 在其所有连续性点的Fourier级数和的方式来解释极限(1)。这种方法涉及 f 的Fourier级数的部分和的合适平均值。
最后,我们也可以在均值平方的意义上定义极限(1)。在下一章,我们将证明,假如f 仅仅可积,则就有
( 当
时 ) 。
有趣的是,我们知道,Fourier级数逐点收敛问题在1966年被L. Carleson解决,此外,他还证明了假如 f 在我们所指的意义上可积(注:Carleson的证明实际上适用于更广泛函数类,这些函数在Lebesgue意义上是平方可积的),则f 的Fourier级数收敛于f (除了可能在“0测度(measure 0)”集上)。这个定理的定明很困难,超出了本书的范围。
2. Fourier级数的唯一性
如果我们假设函数f 的Fourier级数在某个合适的意义上收敛于f,则我们可以推断,此函数由其Fourier系数唯一确定。这可以导出以下推论:假如 f 和 g具有相同的Fourier级数,则 f 和 g 必定相等。取其差 f – g ,则这个主题可重述为:对于所有 n∈ℤ ,假如 , 则 f = 0 。正如所述,这个结论不可能毫无条件地正确,因为,计算Fourier级数要求积分,我们可以看到,例如,任意两个在有限多个点处不同的函数具有相同的Fourier级数。然而,我们确实有下面的这种“积极”的结果。
定理2.1 假设 f 是满足对于所有 n∈ℤ , 都有 的圆周上的可积函数。则只要 f 在点
处连续,则
。
因此,根据我们所知的可积函数的不连续集,我们可以推断出,f 消失于θ的“大部分”值。
证明:
首先,我们假设 f 是实值函数,使用反证法论证它。为了不失通用性,假设 f 定义于闭区间 [-π, π] , 且 ,f ( 0 ) = 0 。现在,我们的思想是构建一个“峰值(peak)”在0点的三角多项式族
,因此,随着
,
。 这将是我们预期出现的推导矛盾 ,因为,根据假设,这个积分等于0 。
因为 f 在0点是连续的,我们可以选择 0 < δ < π/2,使得只要 |θ|< δ ,就有f (θ)< f (0)/2 。令
p(θ)= ε + cos(θ) ,
其中,选取的ε > 0 小到使得只要 δ ≤ |θ| ≤ π,就有| p(θ)| < 1 - ε/2。则,选取一个正数 η < δ,使得对于 |θ|<η,有 p(θ) ≥ 1 + ε/2 。最后,令
,
并选取 B,使得对于所有的θ,都有| f(θ)|≤ B 。这是可行的,因为 f 是可积的,因此是有界的。下图3展示了函数族 的图像。
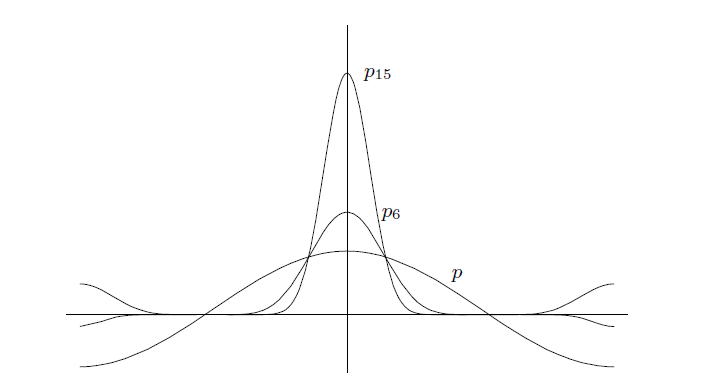
----------------------------当 ε = 0.1时的函数 ,
和
的图像------------------------------------
根据构造,每个![]()
都是一个三角多项式,且因为对于所有 n,都有
。则对于所有的k,我们一定有
。
然而,我们可以估算
。
此外,我们选择的 δ 确保了对于任意 |θ|< δ,f (θ) 和 p(θ)都是非负数,因此
。
最后,
。
因此,当 时,
, f 为实值函数时的证明到此结束。通常,函数
, 其中的u和v是实数。假如我们定义
,则
和
,
因为, ,我们可以推断,u 和 v 的所有Fourier系数都消失了。因此,函数 f 在其连续点处等于0。构建在原点处达到峰值的函数族(在本例中为三角多项式)的想法,以及其他良好的属性,将在本书中发挥重要作用。 此类函数族将在第 4 节后面与卷积概念相关的部分讨论。现在,请注意上面的定理意味着以下内容。
推论(Corollary) 2.2 假设 f 在圆周上连续,且满足对于所有 n∈ℤ , 都有 ,则 f = 0。
下一个推论表明,对于早先阐述的问题(1)而言,在Fourier系数级数绝对收敛的假设下,具有一个简单的肯定答案。
推论(Corollary)2.3 假设 f 在圆周上连续且其Fourier级数绝对收敛,且 。则,Fourier级数一致收敛于 f , 即,
在变量θ上是一致的。
证明:
回忆一下,假如一个连续函数序列一致性收敛,则其极限也连续。现在,注意观察,假设条件 意味着 f 的Fourier级数的部分和绝对且一致性收敛,因此,由
定义的函数g(θ)在圆周上连续。此外,g(θ) 的Fourier系数完全等于
, 因为我们可以将无穷和与积分(级数一致收敛的结果)交换位置。因此,将前面的推论应到的函数 f - g 得产生 f = g ,这正是我们想证明的结果。施加什么条件于f 才可以确保其Fourier级数绝对收敛呢?正如所证明的那样,f 的平滑性与Fourier系数的下降(decay)直接相关,通常,函数越是平滑,其Fourier系数下降越快。结果,我们可以预期相对平滑的函数等于它们的Fourier级数。正如我们现在展示的那样,事实就是如此。
为了准确地描述这种结果,我们引入了标准的 “O” 记法,我们将在本书剩余章节自由地使用这种记法。例如,当 时,表达式
指的是,左侧以右侧的常数倍为界;即,存在
,且对于任意大的
有
。更一般地,当
时,
指的是,对于某个常量C,当x 趋近于 a 时,
。特别地,
指的是
有界。
推论(Corollary)2.4 假设 f 是圆周上的二次连续可微函数。则,当 时,有
,使得 f 的Fourier级数绝对一致收敛于 f 。
证明:
对于 n ≠ 0 ,通过两次分部积分证明基于Fourier系数的计算。我们得到
,
因为 f 和 f ’ 是周期函数,因此方括号中的项消失了。因此
,
其中,C是独立于 n 的常量。(我们可以取C = 2πB ,其中,B 是 f ’’ 的一个边界。) 因为级数 收敛,因此这个推论的证明完成。
顺便说一句,我们已经建立了下面的重要恒等式:
,
假如 n ≠ 0 ,则证明如上,假如 n = 0,将证明留作练习让读者证明。因此,假如 f 可微且 (译注:表示 f 的Fourier级数) , 则
。此外,假如 f 是二次连续可微的,则
,等等。f 上更进一步的平滑意味着Fourier系统数甚至更快的下降。
还有一个推论2.4的加强版,例如,可以证明,仅需假设 f 具有一阶连续导数,则 f 的Fourier级数绝对收敛。甚至,更一般地,假如 f 满足一个α 阶HÄolder条件(HÄolder condition)(其中,α > 1/2) ,则 f 的Fourier级数绝对收敛。即,
(对于所有t ) 。
关于 HÄolder 条件的更多事项,请参见第3章后面的练习题。
在这一点上值得引入一个通用的符号:假如 f 是 k 次连续可微的,则我们说 f 属于类 。属于类
或满足HÄolder条件是描述函数平滑(smoothness)的两个可行的方式。
3. 卷积(Convolutions)
两个函数的卷积概念在Fourier分析中起着根本性的作用;它很自然地出现在Fourier级数的背景下,但更是普遍服务于函数分析的其它场景。(译注:convolution[ˌkɒnvəˈluːʃn] n. 这个词始于1540年代,其词义为“state of being rolled upon itself; a turning, winding, fold, or gyration (自卷状态;转支、缠绕、折叠或旋转(回转))”,来自拉丁语“convolutus”的状态名词,“convolvere ”的过去分词,词义为“to roll together(一起滚动或卷动)”,来自“con-”( com-的变体)(“with,together(伴随、一起)”)+“volvere ”(“to roll(滚动或卷动)”),词义“act of rolling or winding together(一起滚动或缠绕的动作)”始于1590年代。)
已知实数域 ℝ上的两个2π周期函数 f 和 g,我们在闭区间 [-π ,π]定义它们的卷积为
(2) 。
以上的积分使得对于每一个 x 都有意义,因为两个可积函数的乘积仍然可积。此外,因为函数具有周期性,我们可以改变变量写成
。
粗略地说,卷积对应“加权平均(weighted averages)”。例如,在 (2) 中,假如 g = 1,则 f * g 是常量且等于 , 我们可以将其解释为圆周上的函数 f 的均值(译注:前面提到,区间长度为2π的周期函数,总是可以看成单位圆周上的函数)。此外,卷积 ( f * g )( x ) 在某种意义上起着替换这两个函数 f 和 g 的逐点乘积f (x)g(x)的作用。
在本章的背景下,我们对卷积的兴趣缘于函数 f 的Fourier级数的部分和(partial sums)可以表示如下:
,
其中, 是第 n 阶 Dirichlet核(见例子4)为
。
因此,我们注意到,理解 (译注:即函数f 的Fourier级数部分和) 的问题,归结为理解卷积
的问题。
我们以收集卷积的一些主要属性开始。
命题3.1 假设函数 f , g 和 h 是以 2π 为周期的可积周期函数。则:
(i) f * (g + h ) = ( f * g ) + ( f * h ) 。
(ii) ( cf ) * g = c( f * g ) = f * ( cf ) ( 对于任意 c ∈ ℂ )。
(iii) f * g = g * f。
(iv) ( f * g ) * h = f * ( g * h )。
(v) f * g 连续。
(vi) 。
前面4点描述了卷积的代数属性(译注:可交换性(commutative law),可结合性(associative law),可分配性(distributive law),恒等性(identity)(例如,a + 0 = a,a.1 = a),可逆性(inverse)(例如,,
)):可分配性,线性性(可结合性),可结合性。属性(v)展示了一个重要原则:卷积 f * g 比 f 或 g 更加“规则”。因此,是 f * g 连续的,而 f 和 g 仅仅是(Riemann)可积的。最后,(vi)在Fourier研究中是关键。一般情况下,f g 乘积的Fourier系数不是 f 和 g 的Fourier 系数的乘积。然而,(vi)说明,假如我们将函数 f 和 g 的乘积用它们的卷积 f * g 替换,则这种关系就成立。
证明:
从积分的线性线性,立即可推断出(i)和(ii)。
而对于其它属性,假如我们也假设 f 和 g 连续,则不难推断其成立。在这种情况下,我们可以任意地变换积分的次序。例如,为了证实(vi),我们写成
。
为了证明(iii),读者首先应当注意到,假如 F 是以 2π 为周期的连续周期函数,则,对于任意 x ∈ ℝ,有
。
这个恒等式的校验由变量变换 ,再通过转换
构成。则,您可以取
。
此外,可通过交换两个积分符号及合适的变量变换推断出(iv)。
最后,我们可以证明,如果 f 和 g是连续的,则 f * g 是连续的。首先,我们可以写成
。
因为 g 是连续的,因此它必定在任何有界闭区间上一致连续。但g也是周期函数,因此,它必定在所有实数域 ℝ 上是一致连续的;已知 ε > 0 ,存在 δ > 0 ,使得,只要 |s-t | < δ , 就有 | g (s)- g (t)| < δ 。则 意味着对于任意的y ,
,因此,有
,
其中,选择的 B 使得对于所有 x,都有 。最终,我们推断出,至少,当 f 和g 是连续函数时,
是连续的,从而这个命题得证。
通常,当 f 和 g 仅连续可积时,我们便可使用当前确立的结论以及下面的引理(lemma)(其证明放在附录中)。
引理3.2 假设函数 f 可积且以B为界。则在圆周上存在一个连续函数的序列 ,使得
和
当 时,
。
使用这个结论,我们可以完成如下的命题证明。应用引理3.2到 f 和 g 可获得近似连续函数的序列 和
。则
。
根据序列 的属性,当
时,
。
因此, 按 x 一致趋近于0 。类似地,
按 x 一致趋近于 0 ,因此,
一致趋近于 f * g 。它推断出 f * g 也是连续的,因此,我们有属性(v)。
接下来,我们证明(vi)。对于每一个固定的n,我们一定有随着 k 趋近于无穷大,
,因为,
一致收敛于f * g 。然而,我们之前求得
, 因为,
和
两者都是连续的。因此
,
最终,我们求得随着 k 趋近于无穷大, 。类似地,
, ,并且,一旦我们令k超向于无穷大,则我们预期的属性可证。最后,属性(iii)和(iv)可按相同论证推断。
4. 好核(Good kernels)
在证明定理2.1的过程中,我们构造了一个三角多项式序列 ,使其函数
的峰值位于原点。因此,我们可以隔离函数f在原点的行为。在这一节,我们回到这样的函数族,但这次采用一种更为通用的场景。首先,我们定义好核的概念,并讨论这些函数的特征属性。然后,凭借卷积,我们证明这些核如何能恢复一个给定的函数。
满足以下属性的圆周上的核族 称为好核族:
(a) 对于所有 ,
。
(b) 存在 M > 0,使得对所有 ,都有
。
(c) 对于每一个 δ > 0 ,当 时,
。
在实践中,我们会遇到 的函数族,在这种情况下,(b)是(a)的结果。我们可以将核
解释为圆周上重量的分布:属性(a)指的是
单位质量赋予整个圆[-π ,π],属性(c)指的是随着n变得无穷大,质量集中于原点附近(注:在极限方面,好核族表示“Dirac δ 函数”,这个术语来自物理学)。图4(a)展示了一个好核族的典型特征。
通过好核与卷积的结合使用,更能突出好核的重要性。
定理4.1 令 为一个好核族,f 为圆周上的可积函数。则只要 f 在x点连续,就有
。
如果 f 处处连续,则以上极限是一致性的。
由于这个结论,有时候称族 为恒等式的一个近似表达。
在前面,我们已经将卷积解释为加权均值。在这个背景下,卷积
是 的均值。其中,权重由
给出。然而,权重分布
随着 n 逐渐变大,其质量集中于 y = 0 点。因此,在积分中,随着
值 f (x) 被赋予整个质量。图4(b)展示了这个特点。
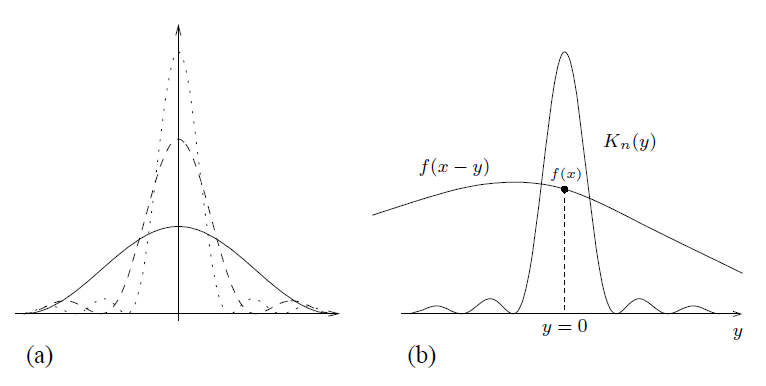
---------------------------------------------------图4 好核--------------------------------------------------
定理4.1的证明:假如 ε > 0 且 f 在 x 点连续,选取 δ 使得 |y|< δ 即意味着 。则,根据好核的第一个属性,我们可以写成
。
因此,
,
其中B是f 的边界。第一项的边界是 ,因为第二个属性是一个好核。根据第三个属性,我们可以看到,对于任意大的n,第二项将会小于ε 。因此,对于某个常量C > 0 以及任意大的n 我们有
,
凭此,就证明了定理中的第一个论断。假如 f 处处连续,则其一致性连续,且δ的选取独立于x 。这就提供了预期的结论,即, 一致趋近于 f 。
回存第三节开头的公式
,
其中, 是 Dirichlet核。现在,我们不禁要问,
是否是一个好核,因为,如果它是一个好核,则定理4.1就意味着,只要 f 在 x 点连续,f 的Fourier级数就收敛于 f ( x )。遗憾的是,并非如此。事实上,估算表明,
违背第二个属性;更准确地说,随首
,您有(见问题2)
。
然而,我们也应当注意到, 作为指数和的公式立即给出
,
因此,好核的第一个属性实际上得到验证。 的均值为1,而其绝对值的积分很大,这个事实是抵消后的结果。事实上,图5展现了函数
呈现正值和负值,且随着N变得超大振荡越激烈。
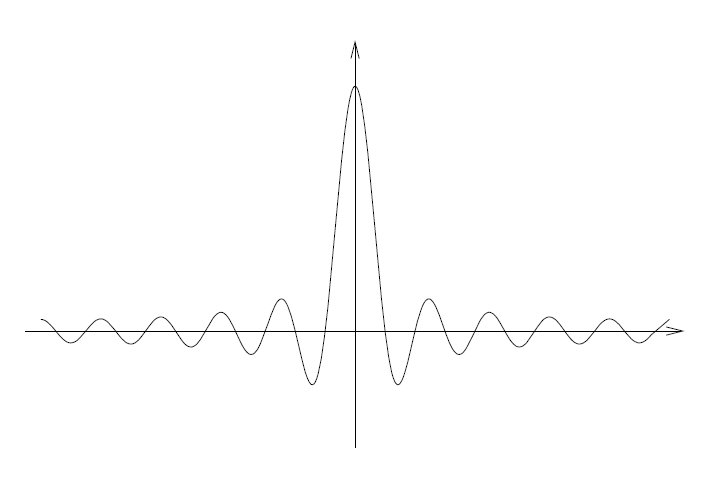
-------------------------------------------图5 N 增大时的Dirichlet核--------------------------------------
这个观察表明,逐点收敛的Fourier级数是错综复杂的(intricate),并且甚至可能在连续点不收敛。我们在下一章将会看到这种情况。
5. Cesàro[tʃeizárou]和Abel[éibəl]可和性(summability):对Fourier级数的应用
因为Fourier级数可能无法在个别点收敛,这就将我们引向尝试按另外一种意义来解释极限
,
从而克服这种不收敛。
5.1. Cesàro均值和求和
我们以普通的部分和均值开始,现在更为详细地描述这种技术。
假如,给予我们一个复数级数
。
我们定义第 n 项部分和为
,
且假如 ,则称级数收敛于s 。这是最自然且最为广泛使用的“可和性”类型。然而,考虑以下级数例子
(3) 。
其部分和形式的序列{1,0,1,0,...}没有极限。因此,读者可以证明,序列的“组限”是1/2,因此,1/2 等于这个“特别”仍限的和。对此,我们给出准确的含义,将前 N 项和的部分和均值定义为
(译注:σ为西腊字母Σ的小写)。
量 称为序列
的前 N 项Cesàro均值或者级数
的前N 项Cesàro和(译注:即,前 N 级数和的均值)(注:注意,假如级数
从k = 1开始,则定义
也是普遍适用的。这种记法的改变对随后的内容没有影响)。
假如 随着N趋向于无穷大而收敛于σ ,则我们称级数
按Cesàro可和于σ (Cesàro summable)。在函数级数的情况下,我们将在逐点或一致收敛的意义上理解极限,这取决于使用场景。
读者很容易验证,在上面的例(3)中,级数Cesàro可和于1/2 。此外,读者可以证明,Cesàro可和是一个比收敛更包容的(inclusive)过程。事实上,假如一个级数收敛于s ,则它也同样Cesàro可和于同样的极限s。
5.2. Fejér[féjeiə]定理
Cesàro可和性的一个有趣的应用出现在Fourier级数的背景下。
我们在前面提到,Dirichlet核不属于好核族。很意外的是,它们的均值是非常好的行为函数,在这个意义上,它们确实构成好核族。
为了理解这个特性,我们构成了Fourier级数的前N 项Cesàro均值,将其定义为
。
因为 ,我们求得
,
其中, 是前 N 项 Fejér 核(Fejér kernel),由
给出。
引理5.1 我们有
,且 Fejér 核是好核。
证明公式 (三角恒等式的简单应用即可)在练习15中有概述。为证明引理的剩余部分,应注意到
是正数且
,鉴于 Dirichlet 核
具有相似的恒等式这一事实。然而,假如
,
,因此,
,因此,可以推断出,当
时,
。
应用定理4.1于这个新的好核函数族则产生随后的重要结论。
定理5.2
假如 f 在圆周上可积,则 f 的Fourier级数在 f 的每一个可连续点Cesàro可和于f 。
此外,假如 f 在圆周上连续,则 f 的Fourier级数一致Cesàro可和于f 。
现在,我们可以陈述两个推论。第一个是我们已经确立的结论。第二个是新的,且具有根本重要性。
推论5.3 假如 f 在圆周上可积,且对于所有 n,有 ,则 f 在其所有的连续点有 f = 0 。
其证明可立证,因为其所有的部分和都为0,因此,其所有的Cesàro均值为0。
推论5.4 圆周上的连续函数可以用三角多项式一致性地逼近。
推论指的是,假如 f 在闭区间[-π, π ]上连续又有f (-π ) = f (π),且 ε > 0,则存在一个三角多项式 P ,使得对于所有的 –π ≤ x ≤ π ,有
。
这直接从定理就能推出,因为部分和是三角多项式(因此,Cesàro均值也是如此)。推论 5.4 是多项式的 Weierstrass 近似定理的周期类比,可以在练习 16 中找到。
5.3. Abel均值与和
事实上,级数的另一种求和方法首要由Abel考虑,事实上早于Cesàro求和法。
对于复数级数 , 如果对于任意 0 ≤ r < 1,级数
收敛,且
,
则称其为Abel可和于s 。
量 A(r) 称为Abel级数均值。读者可以证明,如果级数收敛于s , 则其 Abel 可和于 s。此外,Abel可求和性法甚至比Cesàro可求和法更加强大:当级数是Cesàro可和的时候,它总是Abel可和于同一个和。然而,我们考虑级数
,
则读者可以证明,其Abel可和于 1/4 ,因为
,
但是这个级数并不是Cesàro可和的(见课后练习13)。
5.4. 单位圆盘中的Poisson[pwasɔ́:ŋ]核和Dirichlet问题
为了使Abel可和性与Fourier级数的背景契合,我们定义函数 的Abel 均值为
。
因为索引n 取正负值,则很自然地写成 ,和
,使得Fourier级数的Abel均值对应上一章节的数值级数定义。
我们注意到,因为 f 可积, 按n 一致有界,使得对于任意
,
绝对且一致收敛。正如 Cesàro 均值情况一样,关键事实在于这些Abel均值可以写成卷积
,
其中, 是 Poisson核,由
(4)
给出。
事实上,
,
其中,积分和无限和的变换由级数的一致收敛证明。
引理5.5 假如 0 ≤ r < 1 ,则
。
当r 由下限趋近于1时,Poisson核是好核(注:在这种情况中,核族由连续参数 0 ≤ r < 1 索引,而不是前面考虑的离散n索引。在定义好核的时候,我们只是简单地以r替换n ,按属性(c)取逼近的极限,例如,这种情况就是 r -> 1)。
证明:
恒等式 已经在1.1节中被推导了出来。注意到
。
因此,假如 且
,则
。
因此,当 时,
,
且好核的第三属性得到验证。很显然,
, 且对表达式(4)逐项积分(由级数绝对收敛证明)得到
,因此,推断出证明,
是好核。
将此引理与定理4.1结合在一起,我们就得到了我们的下一个结论。
定理5.6 圆周上的可积函数 f 的Fourier级数在其每一个连续点都Abel可和于f 。 且,假如 f 在圆周上连续,则 f 的Fourier级数一致Abel可和于f 。
现在,我们回到第一章中讨论的问题,我们在圆周上绘制了具有边界条件 u = f 的单位圆盘中稳态热传导方程 Δu = 0 的解。我们按极坐标描述了 Laplace 算子,分离变量,以及由
(5) 给出的预期解,
其中, 是 f 的第 m 项 Fourier系数。换句话说,我们被引向
。
现在,该是我们证明这个等式成立的时候了。
定理5.7 令 f 为定义在单位周周上的可积函数。则由Poisson 积分
定义的单位圆盘上的函数 u 具有以下属性:
(i) u 在单位圆盘上具有两次连续导数且满足Δu = 0 。
(ii) 假如θ是函数 f 的任意连续点,则
。
假如 f 处处连续,则极限是一致性的。
(iii) 假如 f 连续,则 u(r, θ) 是单位圆盘上满足条件(i)和(ii)的稳态热传导方程的唯一解。
证明:
对于(i), 我们记得,其函数 u 由(5)给出。固定ρ < 1 ;在每一个中心点位于原点,半径 r < ρ < 1 的圆盘内部,针对 u 的级数可以逐项微分,且微分级数绝对且一致收敛。因此,u 可以微分两次(事实上,可以微分无限多次),且因为这对所有ρ < 1 都成立。我们推断出 u 在单位圆盘内部是二次可微的。且在极坐标中,
因此,逐项微分证明Δu = 0 。
(ii) 的证明是前面定理的简单应用。为了证明(iii),我们按随后的步骤论证。假设v作为圆盘上稳态热传导方程的解,且随着r从其下限趋近于1而一致收敛于函数 f 。对于每一个位于 0 < r < 1 之间的固定r ,函数 v(r, θ)具有Fourier级数
, 其中
。
很显然,v(r, θ)是方程
(7)
的解。我们求得
(8) 。
事实上,我们可以首先用 乘以 (7) 并按θ积分。则,因为 v 是周期函数,分部二阶积分给出
。
最后,我们可以交换微分和积分的次序,这是允许的,因为,v 有二阶连续导数;这样就产生了(8)。
因此,对于某两个常量 和
,我们一定有
,其中 n ≠ 0 。为了估算这种常量,首先我们应注意到,
的每一项都是有界的,因为v是有界的。因此,
。为了求得
,我们令 r ->1。因为v 随着 r ->1 而一致收敛于函数 f ,我们求得
。
按照类似的论证,这个公式在 n = 0 时也成立。我们的结论是,对于每一个位于 0 < r < 1 之间的r , v的Fourier级数由级数u(r, θ)给出,因此,根据连续函数Fourier级数的唯一性原理,我们一定有 u = v。
评注:根据定理的第(iii)部分,我们可以推断出,如果 u 是圆盘上Δu = 0 的解,且随着 r ->1 而一致收敛,则 u 一定恒等于0 。然而,如果一致收敛用逐点收敛代替,则结论不成立;参见练习18。
内容来源:
<<Fourier Analysis: An Introduction>> E.M. Stein & R. Shakarchi









![[ poi-表格导出 ] java.lang.NoClassDefFoundError: org/apache/poi/POIXMLTypeLoader](https://img-blog.csdnimg.cn/9a58a80cfdd74c468fd9bd01174fb619.png)