蓝桥杯动态规划-第五弹最大子数组和买卖股票最佳时机IV 第N个泰波那契数环形数组

一、最大子数组和

二、买卖股票最佳时机IV

三、第N个泰波那契数

四、环形数组

一、最大子数组和

1.状态表示

dp[i]:到第i数字，所有的最大和。

2.状态转移方程

dp[i]=max(dp[i-1]+p[i]，p[i])(加入这个点是0）

我们来想一下，这个数组分为两种情况，要不他这个连续子数组长度只是一个，这样他就只是p[i],要不他这个数组长度不是一个，这样他就需要看他前面的i-1这个元素，当i-1位置的时候，dp[i-1]就是最大和（可能我们会陷入一个误区，认为这个数组，假如i-1位置是负数，那么肯定是不选i-1位置最好啊。那么假如我们不选这个i位置，他也就相当于连续数组断开了，他就是单个的数组。

3.初始化

最开始的必须要选择，所以说就是nums[0]

4.填表顺序

从左到右

5.返回值

return 返回dp表中最大值即可
class Solution {public int maxSubArray(int[] nums) {int m=nums.length;int []dp=new int[m];if(m==1){return nums[0];}dp[0]=nums[0];for(int i=1;i<m;i++){dp[i]=Math.max(dp[i-1]+nums[i],nums[i]);}int ret=-0x3f3f3f3f;for(int i=0;i<m;i++){ret=Math.max(ret,dp[i]);}return ret;}
}

二、买卖股票最佳时机IV

买卖股票最终弹

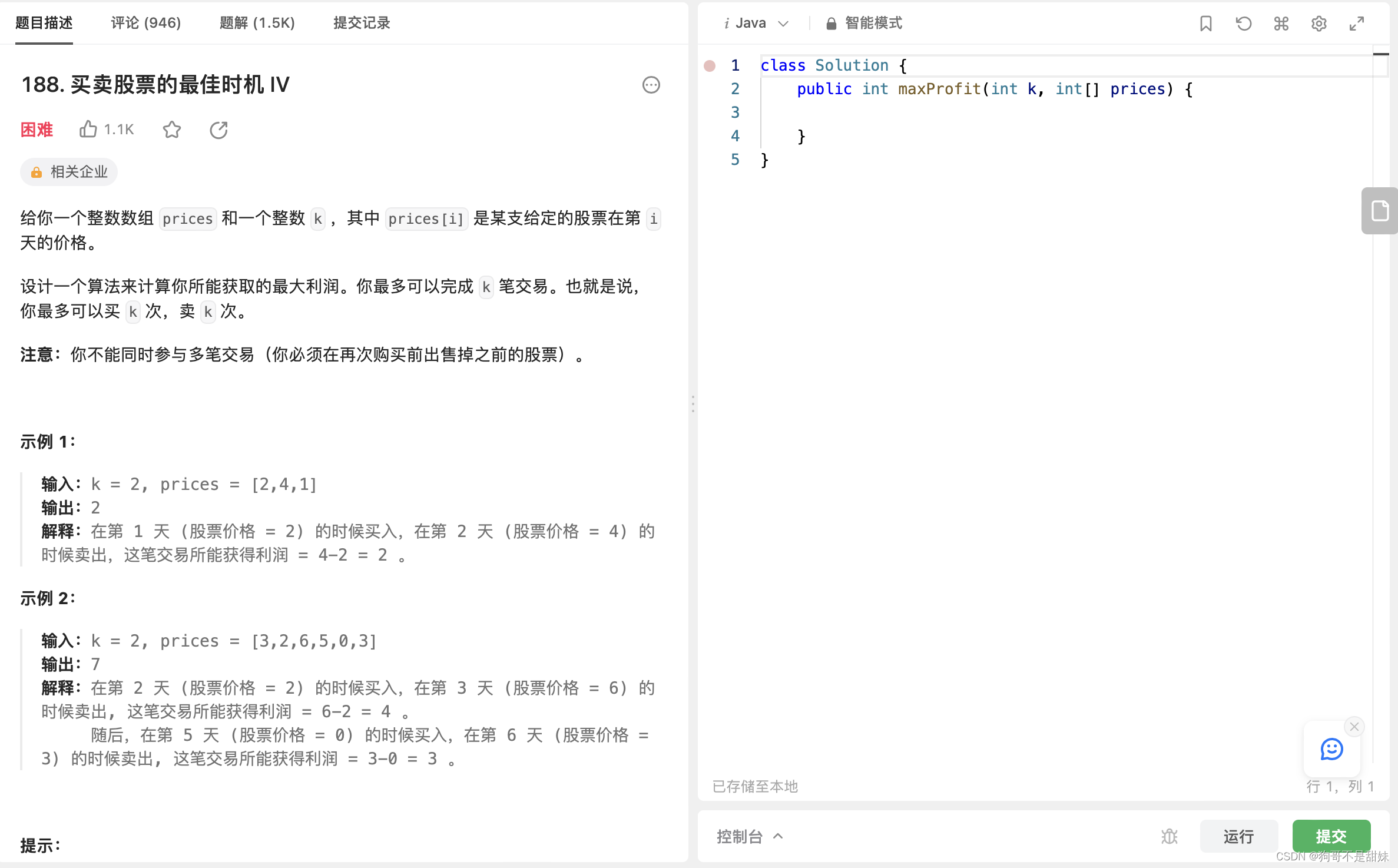
1.状态表示

f[i][k]:第m天处于已经买入但是没有卖出状态，第k笔交易所获的第最大利润

g[i][k]:第m天处于已经卖出但是没有买入的状态，第k笔交易所获的第最大利润

2.状态转移方程

f[i][j]=Math.max(f[i-1][j],g[i-1][j]-prices[i]);

g[i][j]Math.max(g[i-1][j],f[i-1][j-1]+prices[i]);

3.初始化

我们可以观察到g[][]=只有一个地方是等于j-1,那么也就是说，我们只需要初始化一个地方就可以,也就是只要初始化i就行，至于j我们将进行单独的操作

g[i][j]= g[i-1][j];

if(j-1>=0){

g[i][j]= Math.max(g[i-1][j],f[i-1][j-1]+prices[i]);

这个地方最有细节的地方要讲一下，怎么样，才算交易一次，我们这里面的交易一次，是需要卖出，而不是买入就算一次交易，因为如果这么算的话，初始化就和我们之前所进行的操作不同了，只有当卖出后，才算一次交易

f[0][0]=-prices[0];

g[0][0]=0;

假如你想的是买入就算一次，

下面这个式子才应该是正确的，因为第0次，其实并不算一次，所以我们也需要定到k+1，这样他的下标才是k

如果你想要定义只有k ,那么就要我们去思考怎么去更好的表达状态。f我认为它是属于交易之内的东西，所以，他也就不会出现直接交易一次，而是开始0下标的时候就出现，加入是交易一次，那么f在第0天的时候就应该是1了

4.填表顺序

从左到右，两个表一起填写
class Solution {public int maxProfit(int k, int[] prices) {int m=prices.length;k = Math.min(k, m / 2);int f[][]=new int[m][k+1];int g[][]=new int[m][k+1];for(int i=0;i<=k;i++){f[0][i]=g[0][i]=-0x3f3f3f3f;}f[0][0]=-prices[0];g[0][0]=0;for(int i=1;i<m;i++){for(int j=0;j<=k;j++){g[i][j]= g[i-1][j];f[i][j]=Math.max(f[i-1][j],g[i-1][j]-prices[i]);if(j-1>=0){g[i][j]= Math.max(g[i-1][j],f[i-1][j-1]+prices[i]);}}}int ret=0;for(int i=0;i<=k;i++){ret=Math.max(ret,g[m-1][i]);}  return ret;}
}

三、第N个泰波那契数

第N个泰勒那数

1.状态表示

dp[i]:以i位置结尾的，第i个泰波那契数。

2.状态转移方程

dp[i]=dp[i-1]+dp[i-2]+dp[i-3]

3.初始化

dp[0]=0,dp[1]=1,dp[2]=1;

4.填表顺序

从左到右

5.返回值返回dp[n]
class Solution {public int tribonacci(int n) {
//状态表示
int dp[]=new int[n+1];
if(n==0){
return 0;
}else if(n==1||n==2){return 1;
}dp[0]=0;dp[1]=1;dp[2]=1;for(int i=3;i<=n;i++){dp[i]=dp[i-1]+dp[i-2]+dp[i-3];
}return dp[n];}
}

四、环形数组

1.状态表示

dp[i]:到第i位置，返回的非空数组最大和

2.状态转移方程

dp[i]=max(dp[i-1]+p[i]，p[i])

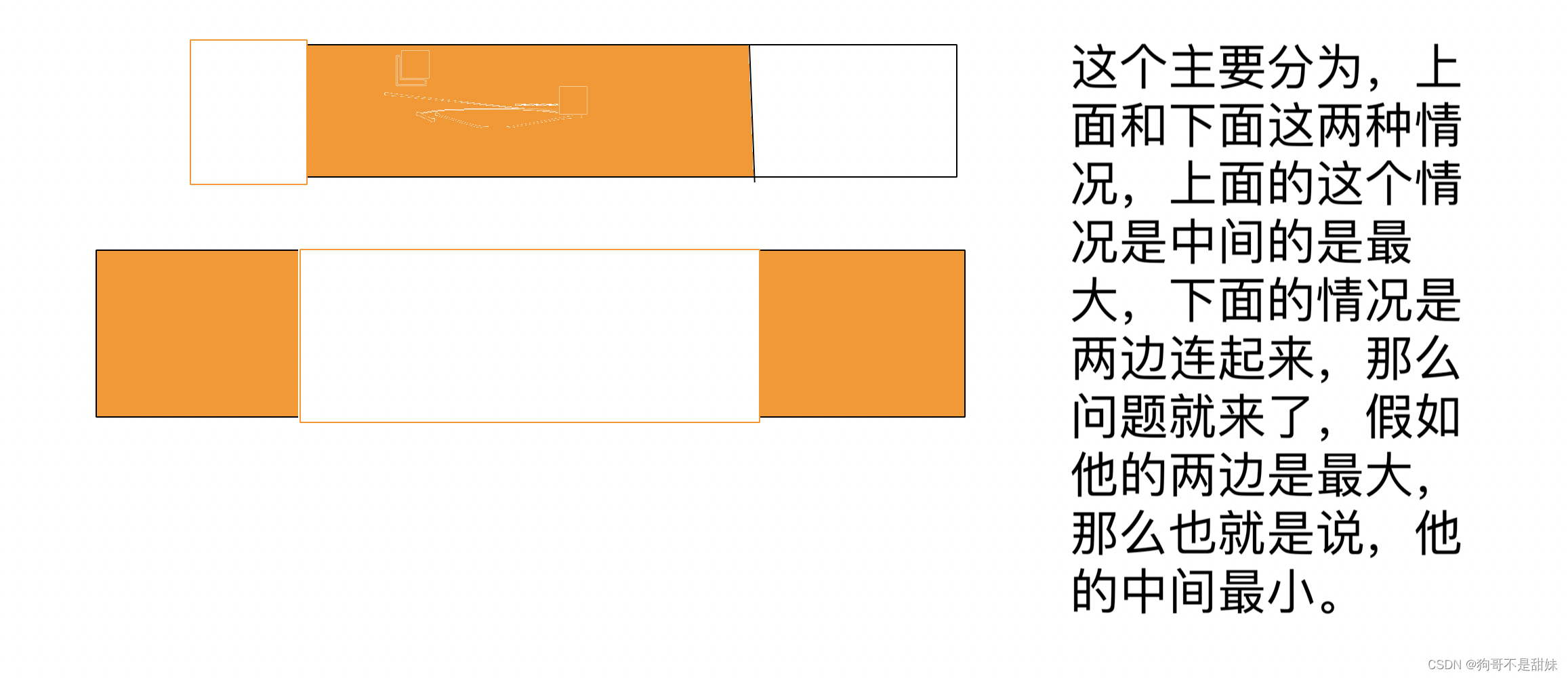
这个题的难点就是在于他的数组一前一后那种值怎么处理，就是

既然它分为这两种情况，那么我们的状态表示也要重新制定一下

1.f[i]:表示到达i位置，最大的数组和。

2.g[i]:表示到达i位置，最小的数组和。

f[i]=Math.max(f[i-1]+p[i],p[i])

g[i]=Math.min(g[i-1]+p[i],p[i])

3.填表顺序

从左到右，两个表一起填写

4.初始化

开始的时候 f[0]=nums[0];
g[0]=nums[0];简单粗暴即可

5.返回值，返回ret
class Solution {public int maxSubarraySumCircular(int[] nums) {int m=nums.length;int []dp=new int[m];int sum=0;for(int i=0;i<m;i++)
{sum=nums[i]+sum;
}    if(m==1){return nums[0];}int []f=new int[m];int []g=new int[m];f[0]=nums[0];g[0]=nums[0];for(int i=1;i<m;i++){f[i]=Math.max(f[i-1]+nums[i],nums[i]);g[i]=Math.min(g[i-1]+nums[i],nums[i]);}int ret=-0x3f3f3f3f;for(int i=0;i<m;i++){
//这个操作，是针对特殊情况，比如说，全是负的-3,-2,-3,这个情况的时候，sum==g[i]也就是说最小值等于总和，这样我会对这个进行处理，ret和f[i]做比较if(sum-g[i]==0){ret=Math.max(ret,f[i]);continue;}ret=Math.max(ret,Math.max(f[i],sum-g[i]));}return ret;}
}