1解题思路:
首先学会输入二维数组;然后知道如何比较求最大值;最后就是格式问题;
2代码:
#include<stdio.h>
int main()
{int a[3][4];int i,j,max,row,line;for(i=0;i<3;i++){printf("请输入二维数组\n");for(j=0;j<4;j++)scanf("%d",&a[i][j]);}printf("\n");max=a[0][0];for(i=0;i<3;i++){for(j=0;j<4;j++){if(a[i][j]>max){max=a[i][j];row=i+1;line=j=1;}}}printf("max=%d\nrow=%d\nline=%d\n",max,row,line); return 0;
}3运行代码:
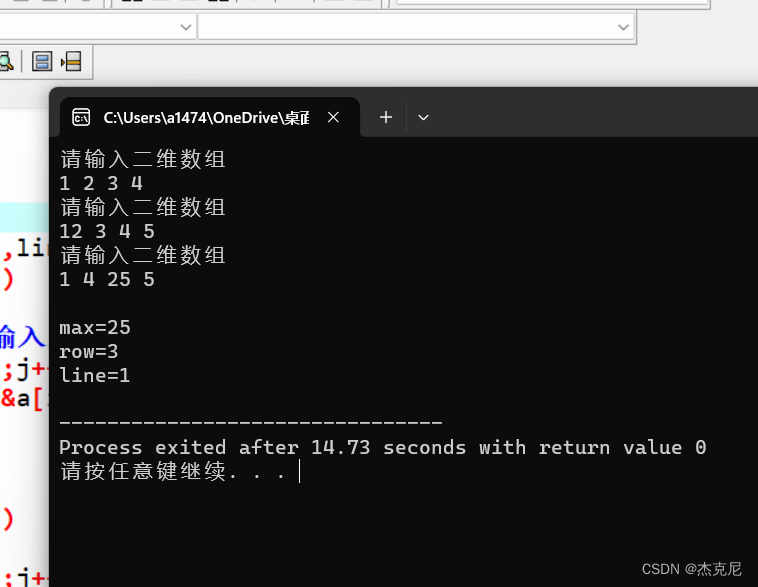
4总结:
感谢各位的阅读,以上就是“C语言怎么有一个 3*4 的矩阵,找出其中值最大的元素,及其行列号”的内容了,经过本文的学习后,相信大家对C语言这一问题有了更深刻的体会,具体使用情况还需要大家实践验证。这里是CSDN杰克尼,小编将为大家推送更多相关知识点的文章,欢迎关注!