二叉树OJ题

---

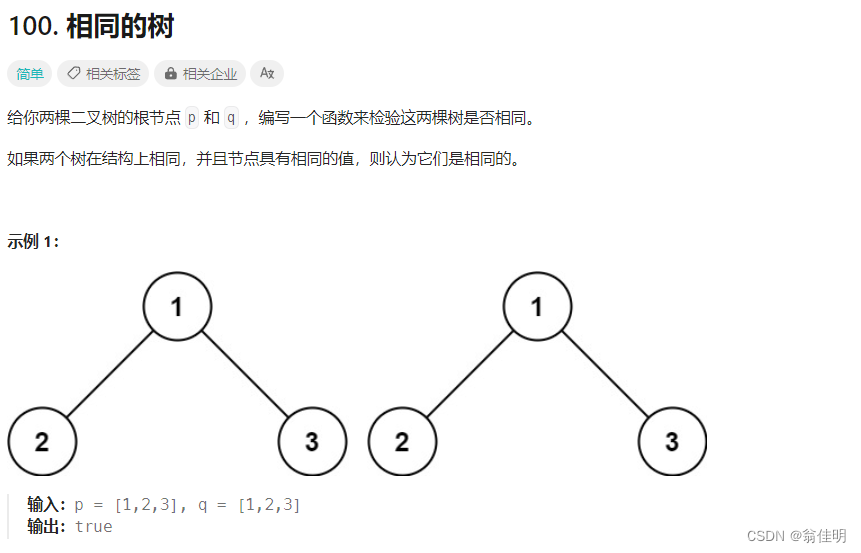
一、 检查两颗数是否相同

1.思路

1.两个树，在保证结构相同的同时，结点的值也要相同

2.一个为空一个不为空，结构不同。都为空，结构相同。都不为空，判断值是否相同

3.先判断根节点是否一样

4.再判断左树是否一样，然后判断右树

2.解题步骤

• 1.判断两棵树的结构是否相同
• 2.如果一个结点为空，一个结点不为空，则证明结构不一致，直接返回false
• 3.结构一致说明都为空，或者都不为空，都不为空包括值相同和值不同两种情况，都为空返回false
• 4.如果都不为空并且值不同，返回ture
• 5.到此，判断好了根节点的情况，先递归左子树，左子树判断完，再递归右子树进行判断
• 6.最后返回，两个子树取到的返回值相与，出现false则返回false
• 时间复杂度：o（min(m,n)）
• 空间复杂的：o (min(m,n))

3.代码

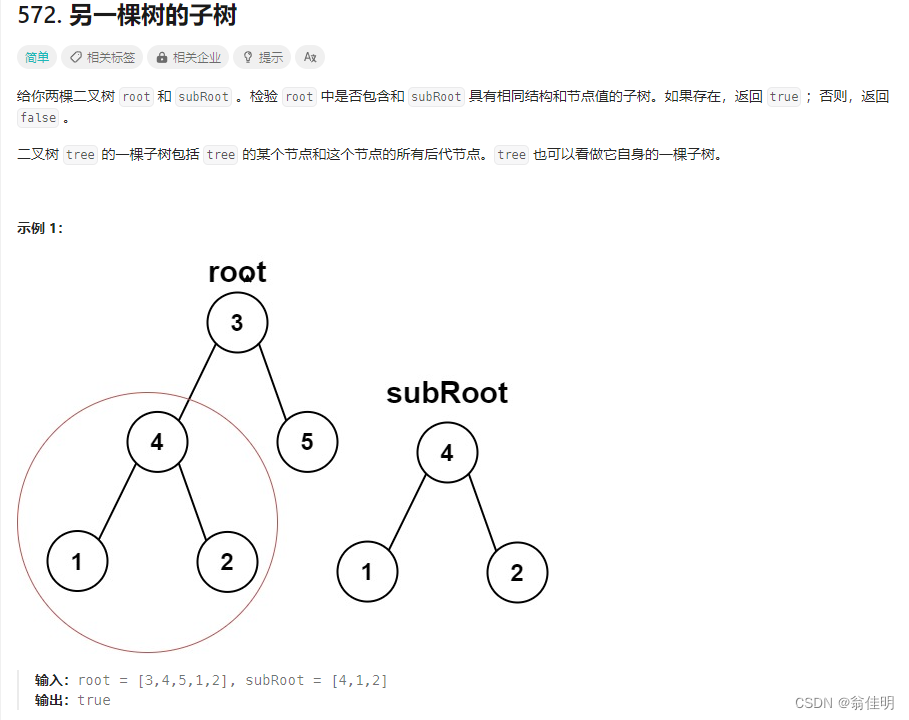
    //判断两棵树是否相同public static boolean isSameTree(TreeNode p, TreeNode q) {if (p == null && q != null || p != null && q == null) {return false;//保证结构相同}//要么都是空，要么都不是空if (p == null && q == null) {return true;//结点都为空，结构一样}if (p.val != q.val) {return false;//结构一样的情况下，值也要相同}//pq都不空且根节点的值都相同return isSameTree(p.left, q.left) && isSameTree(p.right, q.right);//递归得到左右子树返回回来的值}

二、另一棵树的子树

1.思路

0.需要调用刚写的判断两棵树是否相同

1.判断两个树是否完全相同

2.不相同，判断是不是和左子树相同

3.再判断是不是和右子树相同

4.都不相同，返回false

5.当root等于空时返回false，避免发生空指针异常

2.代码

    //判断两棵树是否相同public  boolean isSameTree(TreeNode p, TreeNode q) {if (p == null && q != null || p != null && q == null) {return false;//保证结构相同}//要么都是空，要么都不是空if (p == null && q == null) {return true;//结点都为空，结构一样}if (p.val != q.val) {return false;//结构一样的情况下，值也要相同}//pq都不空且根节点的值都相同return isSameTree(p.left, q.left) && isSameTree(p.right, q.right);//递归得到左右子树返回回来的值}//另一棵树的子树public boolean isSubtree(TreeNode root, TreeNode subRoot) {if (root == null){return false;//避免空指针异常}if ( isSameTree(root,subRoot)){return true;//先判断两个树是否完全一样}if (isSubtree(root.left,subRoot)){return true;//判断是不是和左子树相同}if (isSubtree(root.right,subRoot)){return true;//判断是不是和右子树相同}return false;//没有找到，返回false}

• 时间复杂度：o ( s * t )
• 空间复杂度：o (Max (ds , dt ))

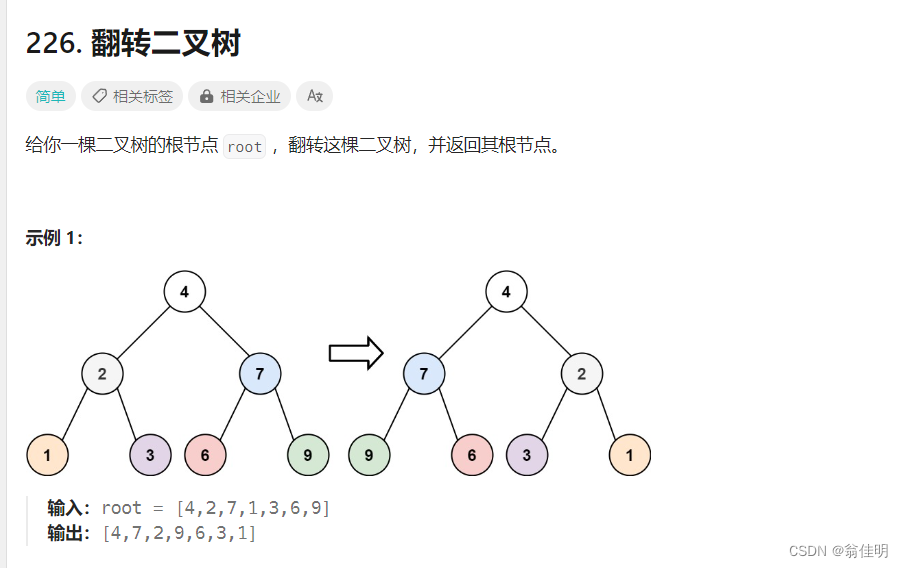
三、翻转二叉树

1.思路

1.翻转整棵树

2.先把根节点的左子树和右子树交换

3.再交换子树上的子树

2.解题步骤

• 先判断该树是否为空
• 不为空，用tmp存储左孩子
• 交换根结点的左子树和右子树
• 先交换左子树中的左右子树，再交换右子树当中的
• 最后翻转完成，返回根结点

3.代码

    //翻转二叉树public TreeNode invertTree(TreeNode root) {if (root == null){return null;}TreeNode tmp = root.left;//根节点的左右树进行交换root.left = root.right;root.right = tmp;invertTree(root.left);//交换左子树中的子树invertTree(root.right);//交换右子树中的子树return root;}

四、判断平衡二叉树

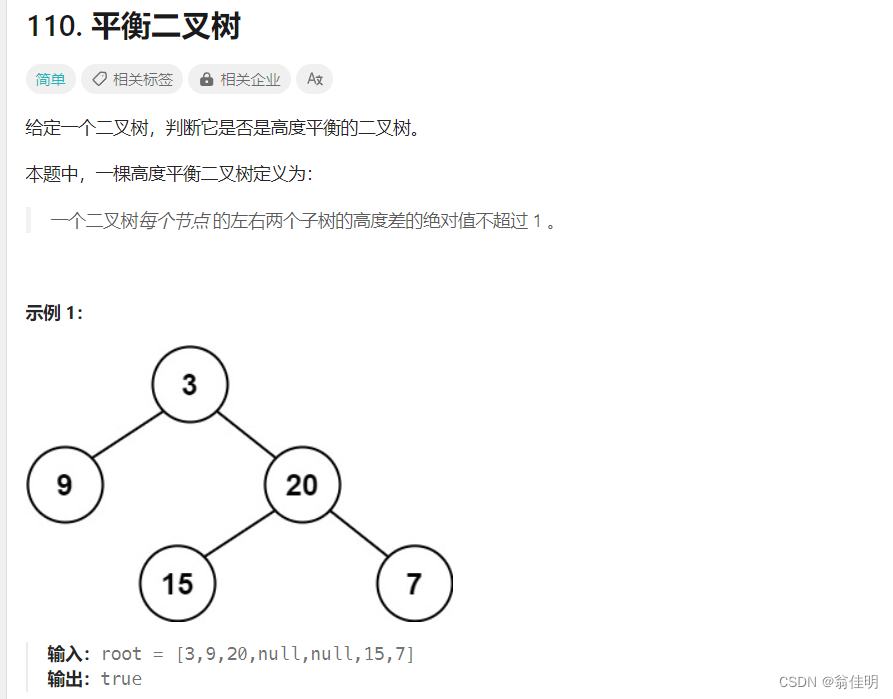
1.思路

1.每个结点都要判断左右子树的高度差的绝对值不超过 1 。也就是说： | 高度差 |<2

2.root为空，返回true

3.左右子树的高度差要小于2

4.左右子树都要保存平衡

2.代码

class Solution {//判断平衡二叉树public boolean isBalanced(TreeNode root) {if (root == null) {return true; //为空，返回true}int leftHeight = maxDepth(root.left);//得到左子树的高度int rightHeight = maxDepth(root.right);//得到右子树的高度return Math.abs(leftHeight - rightHeight) < 2//左右树高度差的绝对值<2&& isBalanced(root.left) && isBalanced(root.right);//并且满足左右子树都是平衡的}public int maxDepth(TreeNode root){//求高度if(root == null){return 0;}int leftHeight = maxDepth(root.left);int rightHeight = maxDepth(root.right);return leftHeight>rightHeight?leftHeight+1:rightHeight+1;}
}

• 时间复杂度：o ( n² ) :求高度的时间复杂度o(n),有n个结点，所以时间复杂度为 n²

如何改成时间复杂度为 o（n）？

1.在求左右树高度的时候，会重复求子树的高度，子树的高度是不断递归返回上来的和，

2.求一个子树的高度时，已经计算过一遍它子树的子树高度，重复计算

3.也就是说，在之前求高度的时候，高度可能已经不平衡了，但是返回的是最大值+1，没有考虑度差的绝对值<2的情况

4.所以可以再求高度的时候，就判断高度差，不平衡直接返回，避免再重复计算

    public boolean isBalanced(TreeNode root) {return maxDepth(root)>=0;//只需要判断返回的值是否>=0}public int maxDepth(TreeNode root){//求高度if(root == null){return 0;}int leftHeight = maxDepth(root.left);if(leftHeight<0){//如果左子树有返回-1的值，说明有不平衡的情况return -1;//不用进入右子树了，直接返回}int rightHeight = maxDepth(root.right);if(rightHeight<0){//如果右子树出现-1,直接返回，不用进行后面的运算return -1;}if(Math.abs(leftHeight-rightHeight)<2){//求高度的时候就判断高度差return Math.max(leftHeight,rightHeight)+1;//符合返回最大值+1}else {return -1;//不符合返回-1；}} }

经过改进，时间复杂度从o ( n² ) 降到了o（n）。

点击移步博客主页，欢迎光临~