目录

543.二叉树的直径

124.二叉树中的最大路径和

2246.相邻字符不同的最长路径

---

543.二叉树的直径

用递归来写 考虑 树形DP 维护以当前节点为根节点的最大值，同时返回给父节点经过当前节点的最大链的长度，这有个trick 当遍历到空节点的时候返回-1 递归进的时候加一个1就好了具体看代码

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:int ans = 0;int dfs(TreeNode*root){if(!root)return -1;int left = dfs(root->left)+1;int right = dfs(root->right)+1;ans = max(left+right,ans);return max(left,right);}int diameterOfBinaryTree(TreeNode* root) {dfs(root);return ans;}
};

124.二叉树中的最大路径和

这个题要我们返回最大路径和，还是考虑递归

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:int ans = -0x3f3f3f3f;int dfs(TreeNode*root){if(!root)return 0;int left = dfs(root->left);int right = dfs(root->right);ans = max(left+right+root->val,ans);return max(max(left,right)+root->val,0);}int maxPathSum(TreeNode* root) {dfs(root);return ans;}
};

2246.相邻字符不同的最长路径

有了前面题目的铺垫，其实还是维护以某点为根节点的最大距离，这里还是用了一个trick，每算一次就取一次最值然后维护最大值，具体可以看这个图来理解

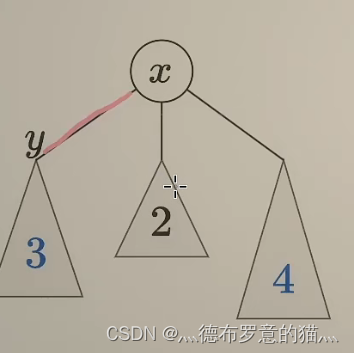（图片引用自灵茶山艾府）

算到3的时候最大值为3 算到2的时候最大值为3+2 并且此时以x为根节点的子树的最长路径为3，遍历到4的时候最大值为3+4 并且更新x为根节点的子树的最长路径为4

然后保证相邻的字符不一样的话加一个判断就好了

const int N = 2e5+10;
class Solution {
public:int e[N],ne[N],h[N],idx;int n;int ans;string tem;void add(int a,int b){e[idx] = b,ne[idx] = h[a],h[a] = idx++;}int dfs(int u,int father){int x_len = 0;for(int i=h[u];~i;i=ne[i]){int j = e[i];if(j==father)continue;int y_len = dfs(j,u)+1;if(tem[j]!=tem[u]){ans = max(x_len+y_len,ans);x_len = max(x_len,y_len);}}// cout<<u<<" "<<x_len<<"\n";return x_len;}int longestPath(vector<int>& parent, string s) {memset(h,-1,sizeof h);tem = s;ans = idx = 0;int n = s.size();for(int i=1;i<n;i++){add(i,parent[i]),add(parent[i],i);}dfs(0,-1);return ans+1;}
};