【数据结构】堆的实现

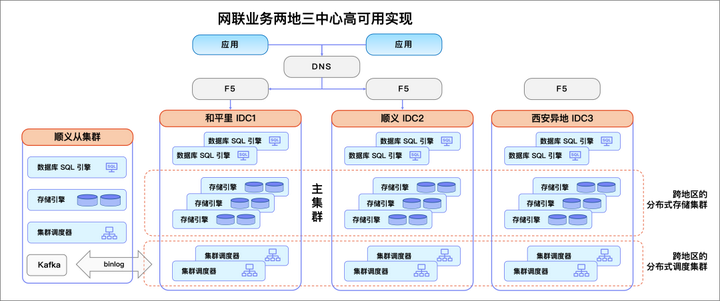
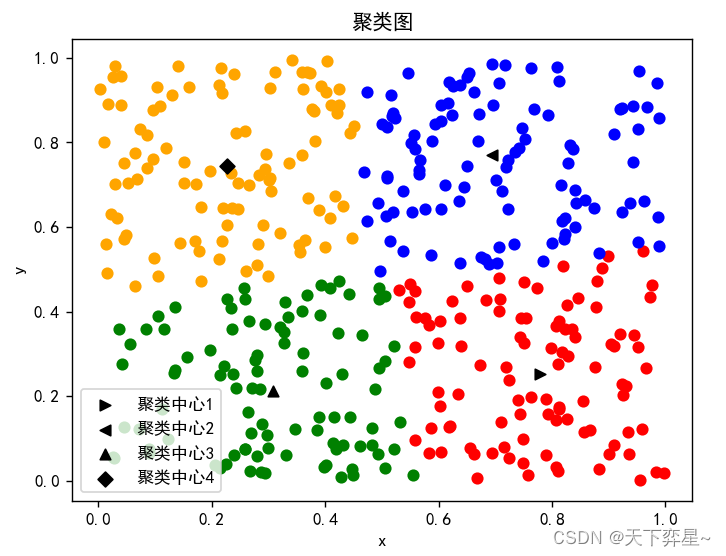
大小堆的概念

将根节点最大的堆叫做最大堆或大根堆，根节点最小的堆叫做最小堆或小根堆。

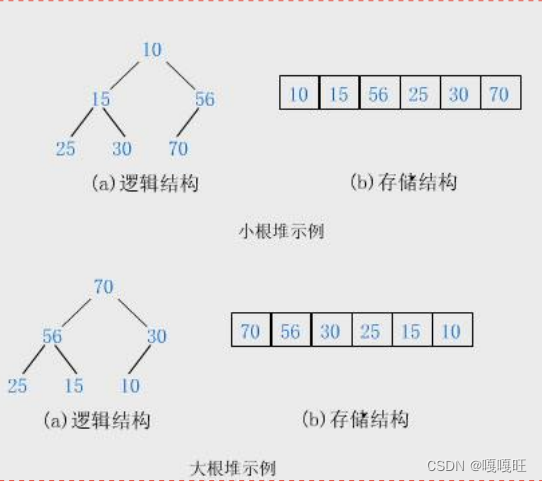
在这里插入图片描述

堆的接口函数

void HeapInit(Heap*st);//堆的初始化
void swap(int* str1, int* str2);//交换两个数据
void Adjustup(int* a, int child);//向上调整
void HeapPush(Heap* st, int x);//插入元素
void AdjustDown(int* a, int n, int parent);//向下调整
bool HeapEmpty(Heap* st);//堆是否为空
int HeapSize(Heap* st);//堆数据个数
void HeapPop(Heap* hp);//堆元素的删除
void HeapDestroy(Heap* st);//堆的销毁
int HeapTop(Heap* st);//堆顶元素

定义堆结构体

typedef struct Heap
{int* a;int size;int capacity;
}Heap;

初始化堆

void HeapInit(Heap*st)
{st->a = NULL;st->capacity = 0;st->size = 0;
}

交换两个数据

void swap(int* str1, int* str2)
{int tmp = *str1;*str1 = *str2;*str2 = tmp;}

判断堆是否为空

bool HeapEmpty(Heap* st)
{assert(st);if (st->size == 0){return true;}else{return false;}}

堆元素的个数

int HeapSize(Heap* st)
{assert(st);return st->size;
}

堆的销毁

void HeapDestroy(Heap* st)
{assert(st);free(st->a);st->a = NULL;st->size = 0;st->capacity = 0;
}

堆顶元素

int HeapTop(Heap* st)
{assert(st);assert(!HeapEmpty(st));return st->a[0];}

向上调整

void Adjustup(int* a, int child)
{int parent = (child - 1) / 2;while (child > 0){if (a[child] < a[parent]){swap(&a[child], &a[parent]);child = parent;parent = (child - 1) / 2;}else{break;}}}

插入数据一般就是插到最后一个，但是插入的数据不能保证该堆还是大堆或者小堆，所以要使用向上调整，举例说明
这是一个小堆
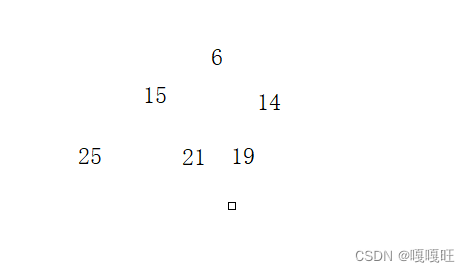
在这里插入图片描述
插入一个数据4后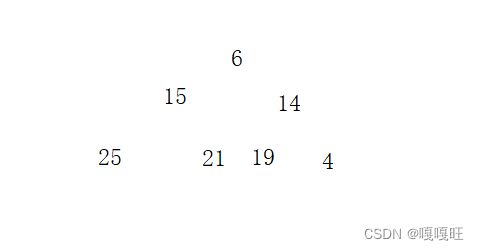

然后就不是堆了，要变成堆，必须将4向上调整，影响的只有他的祖先6和14
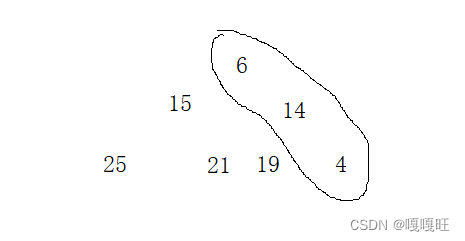
在这里插入图片描述
4作为向上调整的孩子，他的下标为6，他的父亲14，下标为2，
下标对应关系为 parent = (child - 1) / 2
因为是小堆，如果孩子小于父亲的话，交换孩子与父亲的数据

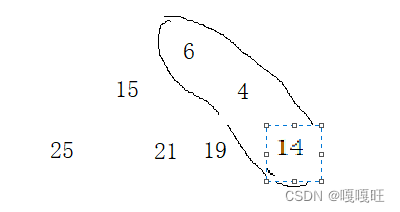
原来父亲与孩子的关系如下

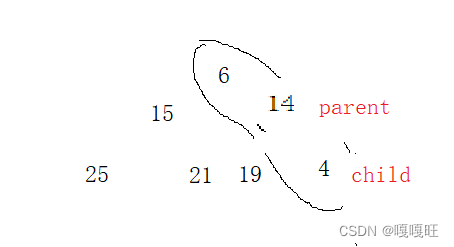
交换父亲和孩子的数据后，改变孩子和父亲的下标如下
在这里插入图片描述
对应操作是 child = parent; parent = (child - 1) / 2;
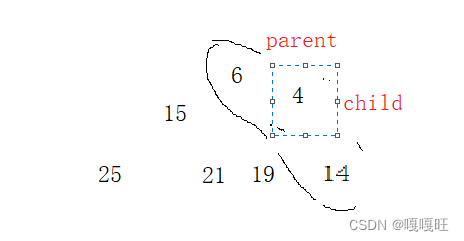
继续比较孩子和父亲的值，如果孩子小于父亲，就交换.

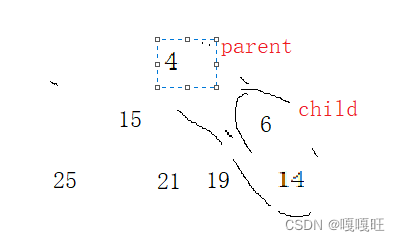
然后改变父亲与孩子的下标改变

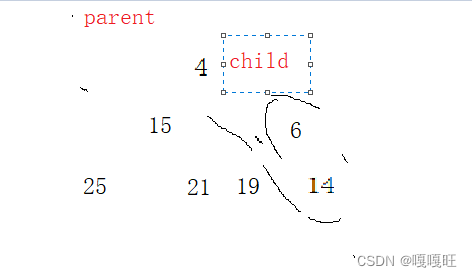
对应操作为 child = parent; parent = (child - 1) / 2;
==注意：当父亲大于孩子时，一直循环，当孩子为堆顶元素时，调整结束，child下标为0，所以循环结束条件为child>0,为什么不用parent<0作为循环结束的条件呢，是因为当child=0时，parent= (child - 1) / 2=0，所以不能用父亲判断.可能在循环过程中遇到父亲小于孩子，这样的话已经成为小堆了.直接break跳出.

插入数据


void HeapPush(Heap* st, int x)
{if (st->capacity == st->size){int newcapcity = st->capacity == 0 ? 4 : st->capacity * 2;int* tmp = (int*)realloc(st->a, newcapcity*sizeof(int));if (tmp == NULL){perror("realloc fail");}st->a = tmp;st->capacity = newcapcity;}st->a[st->size] = x;st->size++;Adjustup(st->a, st->size - 1);
}

每插入一个数据向上调整，随时保证他是小堆

向下调整

void AdjustDown(int* a, int n, int parent)
{int child = parent * 2 + 1;while (child < n){if (child + 1 < n && a[child + 1] < a[child]){child++;}if (a[child] < a[parent]){swap(&a[child], &a[parent]);parent= child;child = parent * 2 + 1;}else{break;}}}

删除数据

void HeapPop(Heap* hp)
{assert(hp);assert(!HeapEmpty(hp));swap(&hp->a[0], &hp->a[hp->size - 1]);hp->size--;AdjustDown(hp->a,hp->size, 0);
}

删除数据我们是删除的堆顶数据，如果直接删掉堆顶数据的话，父子关系全部乱套，就不是堆了.
所以我们采取的是将堆顶元素和堆的最后一个元素交换，然后删除最后一个元素，接着描述堆数据个数的size–;接下来就是要调整堆顶数据，让其保证还是小堆.
比如还是之前的例子
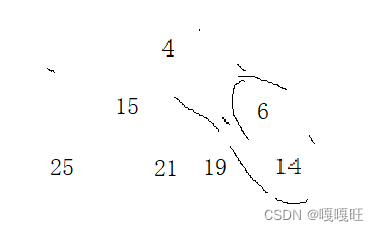
在这里插入图片描述
要删除堆顶元素时，先交换堆顶元素和堆尾元素

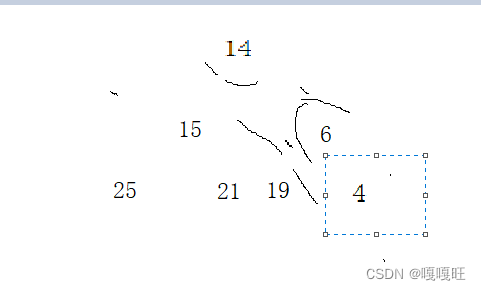
然后删除堆尾元素

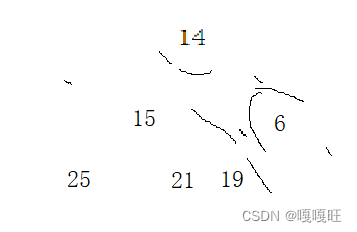
然后选取堆顶元素孩子小的.

if (child + 1 < n && a[child + 1] < a[child]){child++;}

这样保证child下标对应的一定是小孩子，child + 1 < n 这个处理没有右孩子的情况
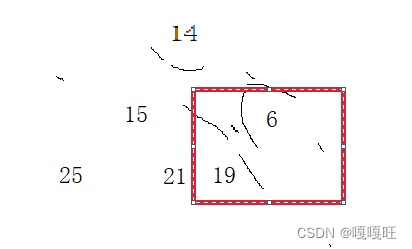
在这里插入图片描述
比如说这里，没有右孩子，child下标范围0-n-1(n为堆数据个数).选出左右孩子中小的，和父亲交换,交换完了，将孩子下标给父亲，孩子的下标更新为孩子的孩子的下标

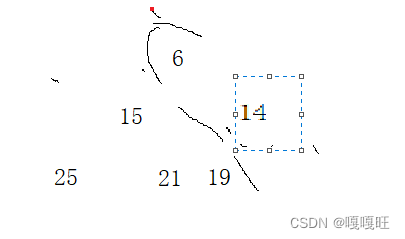
如果只有一个孩子并且父亲大于孩子
则执行这个
在这里插入图片描述
如果孩子大于父亲的话，就已经是小堆了，直接break;
这里循环的条件是child<n,孩子是子叶的时候.

主函数测试

int main()
{Heap  hp;
HeapInit(&hp);
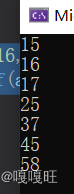
int arr[] = {17,25,15,37,45,16,58};
int sz = sizeof(arr) / sizeof(arr[0]);
int i = 0;
for (i = 0; i < sz; i++)
{HeapPush(&hp, arr[i]);//将数组中的元素压入堆中}
while (!HeapEmpty(&hp))//如果堆不为空
{int top = HeapTop(&hp);//取堆顶元素printf("%d\n", top);//打印堆顶元素HeapPop(&hp);//删除堆顶元素
}return 0;}