目录

树结构及其算法-二叉树遍历

一、中序遍历

二、后序遍历

三、前序遍历

C++代码

---

树结构及其算法-二叉树遍历

我们知道线性数组或链表都只能单向从头至尾遍历或反向遍历。所谓二叉树的遍历（Binary Tree Traversal），简单的说法就是访问树中所有的节点各一次，并且在遍历后将树中的数据转化为线性关系。对于一棵简单的二叉树节点来说，每个节点都可分为左、右两个分支，可以有ABC、ACB、BAC、BCA、CAB和CBA六种遍历方法。

如果按照二叉树的特性，一律从左向右遍历，就只剩下3种遍历方式，分别是BAC、ABC、BCA。这三种方式的命名与规则如下：

1. 中序遍历（Inorder Traversal，BAC）：左子树--树根--右子树
2. 前序遍历（Preorder Traversal，ABC）：树根--左子树--右子树
3. 后序遍历（Postorder Traversal，BCA）：左子树--右子树--树根

对于这3种遍历方式，大家只需要记住树根的位置，就不会把前序、中序和后序搞混了。例如，中序法是树根在中间，前序法是树根在前面，后序法是树根在后面，遍历方式都是先左子树后右子树。

一、中序遍历

中序遍历是“左中右”的遍历顺序，也就是从树的左侧逐步向下方移动，直到无法移动，再访问此节点，并向右移动一个节点。如果无法再向右移动，就可以返回上层的父节点，并重复左、中、右的步骤进行。

1. 遍历左子树
2. 遍历树根
3. 遍历右子树

	void Inorder(TreeNode* tempTree) {if (tempTree != nullptr) {Inorder(tempTree->leftNode);cout << tempTree->data << " ";Inorder(tempTree->rightNode);}}

二、后序遍历

后序遍历是“左右中”的遍历顺序，即先遍历左子树，再遍历右子树，最后遍历（或访问）根节点，反复执行此步骤。

1. 遍历左子树
2. 遍历右子树
3. 遍历树根

	void Postorder(TreeNode* tempTree) {if (tempTree != nullptr) {Postorder(tempTree->leftNode);Postorder(tempTree->rightNode);cout << tempTree->data << " ";}}

三、前序遍历

前序遍历是“中左右”的遍历顺序，也就是先从根节点遍历，再往左方移动，当无法继续时，继续向右方移动，接着重复执行此步骤。

1. 遍历树根
2. 遍历左子树
3. 遍历右子树

	void Preorder(TreeNode* tempTree) {if (tempTree != nullptr) {cout << tempTree->data << " ";Preorder(tempTree->leftNode);Preorder(tempTree->rightNode);}}

C++代码

#include<iostream>
using namespace std;struct TreeNode {int data;TreeNode* leftNode;TreeNode* rightNode;TreeNode(int tempData, TreeNode* tempLeftNode = nullptr, TreeNode* tempRightNode = nullptr) {this->data = tempData;this->leftNode = tempLeftNode;this->rightNode = tempRightNode;}
};class Tree {
private:TreeNode* treeNode;
public:Tree() {treeNode = nullptr;}TreeNode* GetTreeNode() {return this->treeNode;}void AddNodeToTree(int* tempData, int tempSize) {for (int i = 0; i < tempSize; i++) {TreeNode* currentNode;TreeNode* newNode;int flag = 0;newNode = new TreeNode(tempData[i]);if (treeNode == nullptr)treeNode = newNode;else {currentNode = treeNode;while (!flag) {if (tempData[i] < currentNode->data) {if (currentNode->leftNode == nullptr) {currentNode->leftNode = newNode;flag = 1;}elsecurrentNode = currentNode->leftNode;}else {if (currentNode->rightNode == nullptr) {currentNode->rightNode = newNode;flag = 1;}elsecurrentNode = currentNode->rightNode;}}}}}void Preorder(TreeNode* tempTree) {if (tempTree != nullptr) {cout << tempTree->data << " ";Preorder(tempTree->leftNode);Preorder(tempTree->rightNode);}}void Inorder(TreeNode* tempTree) {if (tempTree != nullptr) {Inorder(tempTree->leftNode);cout << tempTree->data << " ";Inorder(tempTree->rightNode);}}void Postorder(TreeNode* tempTree) {if (tempTree != nullptr) {Postorder(tempTree->leftNode);Postorder(tempTree->rightNode);cout << tempTree->data << " ";}}
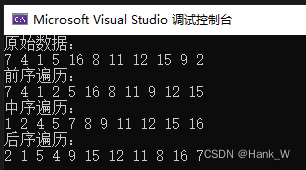
};int main() {int data[]{ 7,4,1,5,16,8,11,12,15,9,2 };cout << "原始数据：" << endl;for (int i = 0; i < 11; i++)cout << data[i] << " ";cout << endl;Tree* tree = new Tree;tree->AddNodeToTree(data, 11);cout << "前序遍历：" << endl;tree->Preorder(tree->GetTreeNode());cout << endl;cout << "中序遍历：" << endl;tree->Inorder(tree->GetTreeNode());cout << endl;cout << "后序遍历：" << endl;tree->Postorder(tree->GetTreeNode());cout << endl;return 0;
}

结果输出