深度学习_3 数据操作之线代，微分

线代基础

标量

只有一个元素的张量。可以通过 x = torch.tensor(3.0) 方式创建。

向量

由多个标量组成的列表（一维张量）。比如 x = torch.arange(4) 就是创建了一个1*4的向量。可以通过下标获取特定元素（x[3]），可以通过 len(x) 获取长度，可以通过 x.shape 获取形状。

矩阵

二维张量，比如 reshape(a,b) 后得到的张量。

可以通过 X.T 转置。

张量运算

相同形状的张量二元运算是标量，向量，矩阵运算的扩展。

加法：所有元素分别求和。

乘法：对应位置元素分别相乘。

加标量/乘标量：所有元素分别加/乘标量。

降维

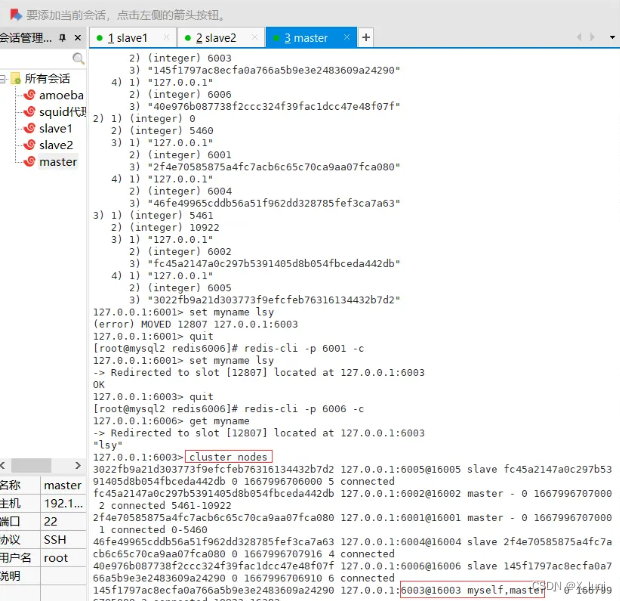
sum() 是可以实现降维操作的。A.sum() 是直接沿所有维度求和得到一个标量。还可以指定维度求和进行降维。

A
# Output
(tensor([[ 0.,  1.,  2.,  3.],[ 4.,  5.,  6.,  7.],[ 8.,  9., 10., 11.],[12., 13., 14., 15.],[16., 17., 18., 19.]]),A_sum_axis0 = A.sum(axis=0)
A_sum_axis0, A_sum_axis0.shape
# Output
(tensor([40., 45., 50., 55.]), torch.Size([4]))A_sum_axis1 = A.sum(axis=1)
A_sum_axis1, A_sum_axis1.shape
# Output
(tensor([ 6., 22., 38., 54., 70.]), torch.Size([5]))A.sum(axis=[0, 1])  # 结果和A.sum()相同
# Output
tensor(190.)

总和也可以用 A.mean() 或者 A.sum()/A.numel() 来算。

也可以利用 A.mean(axis=0) 或 A.sum(axis=0)/A.shape[0] 来降低维度。

非降维求和

sum_A = A.sum(axis=1, keepdims=True)
sum_A
# Output
tensor([[ 6.],[22.],[38.],[54.],[70.]])A / sum_A	# 广播操作
# Output
tensor([[0.0000, 0.1667, 0.3333, 0.5000],[0.1818, 0.2273, 0.2727, 0.3182],[0.2105, 0.2368, 0.2632, 0.2895],[0.2222, 0.2407, 0.2593, 0.2778],[0.2286, 0.2429, 0.2571, 0.2714]])A.cumsum(axis=0)	# 按行求和且不降维
# Output
tensor([[ 0.,  1.,  2.,  3.],[ 4.,  6.,  8., 10.],[12., 15., 18., 21.],[24., 28., 32., 36.],[40., 45., 50., 55.]])

矩阵乘法

左矩阵逐列和右矩阵逐行相乘。

torch.mv(a,b)

范数

向量的大小。

L1范数：各个分量绝对值长度求和。

L2范数：欧几里得长度（比如二维向量是a²+b² 开根）。

Frobenius范数：矩阵中每一个元素的平方和开根。

微积分

微分

导数的基本概念就不详细叙述了，这是大学必修课。

常用公式：

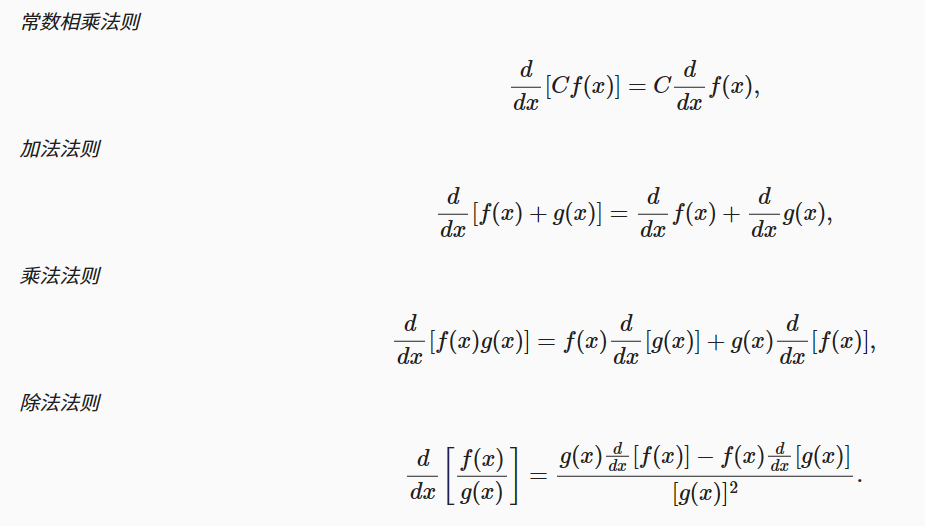
1698756745588

自动微分

python 里是自动求导，一个函数在指定值上做求导。

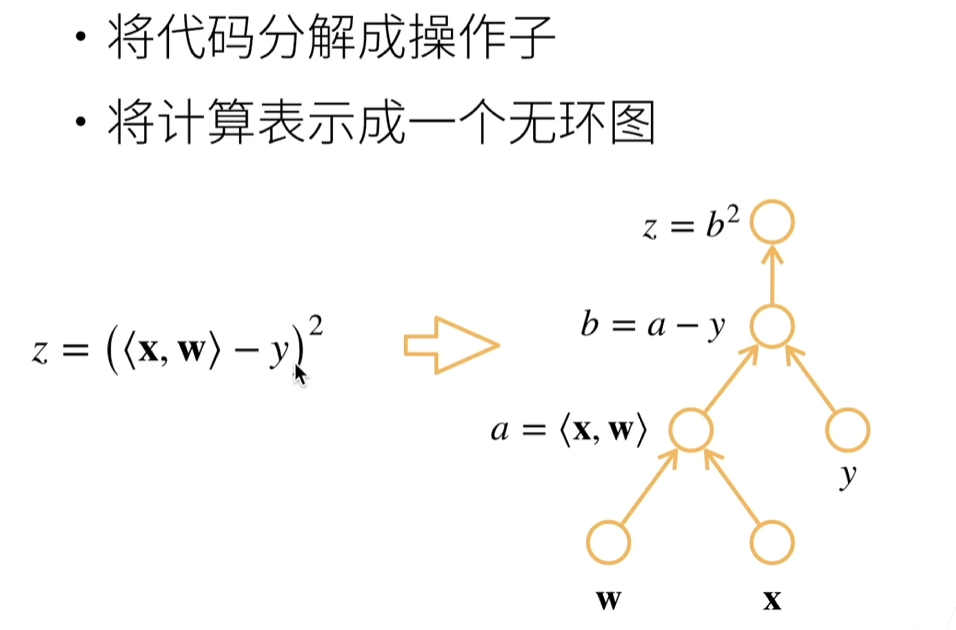
1698811840756

正向传递：如上图，先计算 w 关于 x 的导数，在计算 b 关于 a 的导数……

反向传递：全过程正好相反，先计算 z 关于 b 的导数，再计算 b 关于 a 的导数……

正向反向累积的时间复杂度都是 O(N)，但是正向空间复杂度是 O(1)，反向一直要把所有的中间结果记录下来，空间复杂度 O(N)。

显示构造：先定义公式，再赋值。

1698811994384

隐式构造：pytorch 采用的是这种方案。

1698812013657

下面展开一个具体的计算例子。比如我们要计算 y=2x² 的导数。

# 先创建 x
from mxnet import autograd, np, npx
npx.set_np()
x = np.arange(4.0)	#[0. ,1. ,2. ,3.]
x.requires_grad_(True)  # 等价于x=torch.arange(4.0,requires_grad=True)
# 在计算关于x的梯度后，将能够通过'grad'属性访问它，它的值被初始化为 [0. ,0. ,0. ,0.]
y = 2 * torch.dot(x, x)
y.backward()
x.grad		# [0. ,4. ,8. ,12.]
# y 的导数在这几个点上应该是 4x。验证一下是否正确
x.grad == 4 * x	# [True,True,True,True]# 再算一下另一个函数
x.grad.zero_()	# 清零
y=x.sum()		# x_1+x_2+...+x_n
y.backward()
x.grad			# [1. ,1. ,1. ,1.]x.grad.zero_()	# 清零
y = x * x  # y是一个向量，注意这里是哈马达积，和前面的点积不一样。点积得到的是一个标量，这个是每个x对应彼此相乘得到的1*4的向量
# 等价于y.backward(torch.ones(len(x)))
y.sum().backward()
x.grad  # 等价于y=sum(x*x) [0. ,2. ,4. ,8.]# 分离计算：比如z=u*x, u=x*x，但是我们不想把 u 展开求导，我们期望对 z 求 x 导数得到 u
x.grad.zero_()
y = x * x
u = y.detach()	# 相当于 requires_grad = False，不会得到梯度
z = u * x
z.sum().backward()
x.grad == u# 自动微分也可以计算包含条件分支的分段。以下分段本质上都是k*a。
def f(a):b = a * 2while b.norm() < 1000:b = b * 2if b.sum() > 0:c = belse:c = 100 * breturn c
a = torch.randn(size=(), requires_grad=True)
d = f(a)
d.backward()
a.grad == d / a	# True