PRINET: A PRIOR DRIVEN SPECTRAL SUPER-RESOLUTION NETWORK

（PRINET：先验驱动的光谱超分辨网络）

光谱超分辨率是指直接从RGB图像重建高光谱图像。近年来，卷积网络已经成功地用于这一任务。然而，很少有人考虑到高光谱图像的具体属性。在本文中，我们试图设计一个超分辨率网络，名为PriNET，基于两个先验知识的高光谱图像。第一个是谱相关。根据这一性质，我们设计了一个分解网络来重建高光谱图像。在该网络中，高光谱图像的整个光谱波段被分成几组，并提出了多个残差网络分别重建它们。第二个知识是高光谱图像应该能够生成其对应的RGB图像。受此启发，我们设计了一个自监督网络来微调分解网络的重建结果。最后，这两个网络结合在一起，构成了PriNET。

INTRODUCTION

大多数当前的消费者相机能够通过将场景的光谱映射到三个光谱带（即，红色、绿色和蓝色）。虽然它服从人眼的视觉系统，但许多光谱信息被忽略了。与RGB图像不同（例如，图1（a））、高光谱图像（例如，图1（b））通常包含十个以上的光谱带。这种丰富的光谱信息有利于许多计算机视觉任务，如人脸识别，细粒度识别和对象跟踪。然而，由于成像技术的限制，获取高光谱图像比RGB图像更困难。传统的光谱仪通常以光谱或空间扫描的方式操作，这是耗时的并且设备部署相对昂贵。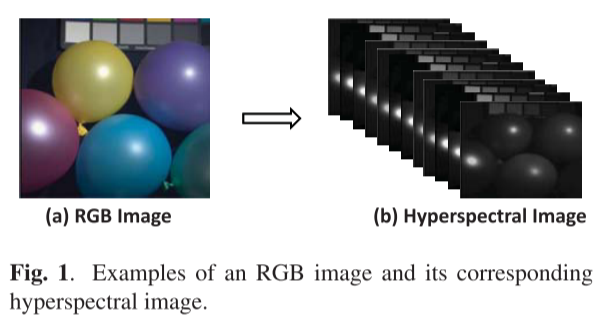
除了从光谱仪直接获取高光谱图像之外，另一种替代方法是通过利用光谱超分辨率算法从相应的RGB图像重建高光谱图像。这是出于观察RGB图像可以被认为是相机光谱灵敏度函数下的高光谱图像的三维投影。光谱超分辨率的关键是对RGB图像与高光谱图像之间复杂的映射关系进行建模。由于这是一个三对多的映射问题，传统的模型通常会加入一些约束来使问题可解，例如稀疏和低秩约束。最近，深度学习在空间超分辨率领域显示出了巨大的力量。受此启发，越来越多的研究人员尝试应用深度网络来学习光谱超分辨率的映射函数。然而，大多数研究都集中在网络的非线性表示能力上，而忽略了高光谱图像的特殊性质。
在本文中，我们提出了一个光谱超分辨率网络PriNET，这是由两个先验知识驱动的高光谱图像。第一个知识是谱相关。由于电磁波谱上的采样沿着密集，高光谱图像中相邻波段往往存在较强的相关性。基于这一性质，我们设计了一个分解网络来重建高光谱图像。在该网络中，首先根据光谱带间的相关性将光谱带划分为若干组。然后，对每一组，我们设计了一个残差网络来重构属于它的光谱带。第二个知识是RGB图像可以被视为对应的高光谱图像的三维投影。因此，从分解网络得到的超分辨率高光谱图像应该能够重建输入的RGB图像。根据这一性质，我们设计了一个自监督网络来微调分解网络的重建结果。这两个网络最终结合在一起，构建端到端的PriNET。

贡献

1）与现有的光谱超分辨率网络不同，我们的网络由高光谱图像的两个特定属性驱动，可以更好地捕捉RGB和高光谱图像之间的关系。
2）基于高光谱图像相邻波段间存在强相关性的先验知识，设计了一种分解网络，将复杂的超分辨率问题简化为多个子问题。
3）由于RGB图像可以被认为是高光谱图像的投影，我们设计了一个自监督网络来微调分解网络的重建结果。

RELATEDWORK

单图像超分辨率是计算机视觉领域的一个活跃的研究课题，其目的是提高输入图像的空间分辨率。光谱超分辨率是一种以提高输入图像的光谱分辨率为目标的图像处理技术，近年来受到了广泛的关注。现有的光谱超分辨方法大致可以分为两类：传统超分辨模型和深度超分辨模型。
Traditional super-resolution models: Arad和Ben-Shahar为高光谱特征创建了一个稀疏字典。给定相机光谱响应，他们使用正交匹配追踪算法从RGB图像重建高光谱图像。类似地，Aeschbacher等人也使用了基于稀疏表示的光谱超分辨率模型，并且实现了比文献[2]更好的重建性能。Jia等人发现自然场景的光谱位于低维流形中，然后提出了一种基于流形的两步光谱超分辨率映射和重建方法。最近，为了充分利用高光谱图像的高维结构，文献[3]提出了一种低秩张量恢复模型。
Deep super-resolution models: 得益于强大的非线性映射能力，近年来深度学习被自然地应用于光谱超分辨率。作为早期的尝试之一，Xiong等人首先对RGB图像的光谱维度进行上采样，然后应用具有全局残差学习策略的卷积神经网络（CNN）从上采样的RGB图像重建高光谱图像。另一个尝试是[13]，它使用跳过连接和密集块来形成超分辨率网络。Shi等人进一步改进了模型，删除了手工制定的上采样算子，并采用残差块来构建HSCNNR模型或采用密集块来构建HSCNN-D模型。在[6]中，采用了一种类似于U-Net的架构来重建高光谱图像。Fu等人将具有1 × 1卷积核的光谱CNN和空间CNN连接起来，以恢复高光谱图像。

METHODOLOGY

如图2所示，我们提出的PriNET主要包括三个阶段。首先，高光谱图像中的光谱波段根据其相关性被分成多个组。然后，提出了一种分解网络，从输入的RGB图像中分别重建每个组。在这个阶段，将这些重建的组连接在一起将生成重建的高光谱图像。最后，设计了一个自监督网络来微调重建结果。

Spectral band grouping

光谱超分辨率的目的是从高光谱图像Y ∈$R^{w\times h\times l}$中重建出相应的RGB图像X ∈$R^{w\times h\times 3}$，其中l表示高光谱图像中光谱波段的数目，w和h分别表示两幅图像的宽度和高度。通常，由于成像阶段的密集光谱采样，Y中的相邻带具有一些相关性。在这里，我们使用相关系数来量化这种关系。具体地说，对于任意两个频带y_i ∈$R^{w\times h}$和y_j ∈$R^{w\times h}$，我们首先将它们向量化为两个向量，然后计算它们的相关系数。然后，我们可以获得Y的维数为l × l的相关矩阵。对训练集中的所有高光谱图像重复整个过程，并导出平均相关矩阵。
基于相关矩阵，我们可以设定一个阈值来对整个光谱带进行分组。作为一个例子，图2展示了从CAVE数据中导出的平均相关矩阵，较亮的值指示较高的相关性。结果表明，相邻谱带之间存在很强的相关性。在本文中，我们经验性地选择0.8作为分组阈值，因此Y可以沿谱域沿着被分成三个不同的组Y₁、Y₂和Y₃。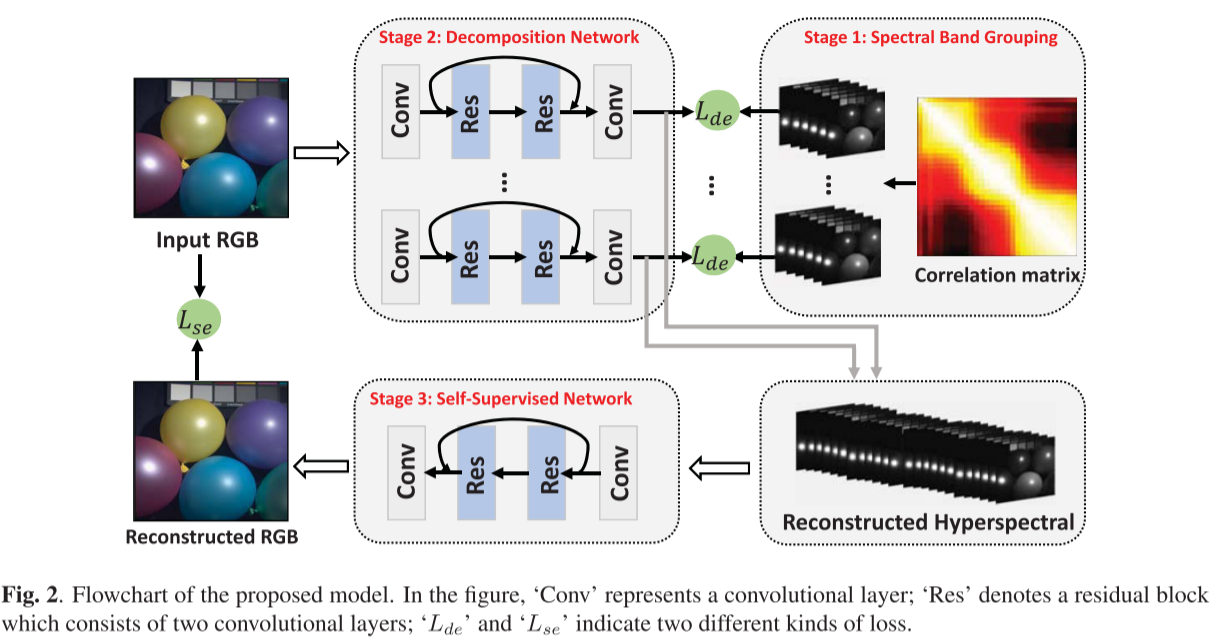

Decomposition network

大多数现有的光谱超分辨率网络试图学习一个端到端映射函数f(x)，使得Y近似f(x)。由于Y包含不同的频谱信息，因此需要非常深的网络来确保f(x)的映射能力。例如，HSCNN-R网络采用34个卷积层来学习f(x);[8]中的重建网络由42个卷积层组成。然而，如在小节3.1中所讨论的，Y中的混合光谱信息可以被解耦成m（例如，本文中m =3）群。因此，我们的分解网络旨在学习m个映射函数，第i个映射函数f_i(x)，i ∈{1，···，m}只负责Y_i（即，Y_i 近似 f_i(x)）。因为Y_i包含类似的光谱信息，所以学习f_i(x)比学习f(x)容易得多。

如图2所示，分解网络由m个分支组成。每个分支具有两个卷积层和两个残差块。第一个卷积层旨在提取特征并将低维RGB图像投影到高维空间中。最后一个卷积层尝试将特征映射的维度减少到所需的维度，这取决于相应组中的光谱带数量。中间的块专注于学习第一个和最后一个卷积层之间的残差。与[7]相同，每个残差块由两个卷积层组成。对于每个卷积层，内核大小设置为3×3。除了最后一个卷积层，每层的卷积核数为64。

Self-supervised network

对于RGB图像，它可以被视为使用相机中的红-绿-蓝三色滤波器的对应高光谱图像的三维投影。受此属性的启发，Kawakami等人提出通过将生成的高光谱图像映射回原始RGB图像来改进其重建结果。映射函数等于给定RGB相机的光谱灵敏度函数。然而，在大多数情况下，关于相机的参数是未知的。此外，RGB图像可以来自不同的相机。因此，直接应用它们的微调策略是不灵活的。考虑到映射过程类似于卷积算子，如之前文献所讨论的，我们设计了一个自监督网络来微调分解网络的重建结果。
图2展示了自监督网络的细节。分解网络的输出首先连接在一起，然后输入到自监督网络。与分解网络相同，自监督网络也包含两个卷积层和两个残差块。每个残差块包括两个卷积层。每个卷积层的内核大小为3 × 3。最后一个卷积层中的核数是3，其他卷积层的核数是64。请注意，除了最后一个卷积层，每个卷积层后面都有一个ReLU层。

Loss functions

分解网络和自监督网络都有各自的损失函数来指导它们的学习过程。假设分解网络中第i个分支的输出为f_i(X;Θ_i)，则对应的损耗值L_de可以计算为：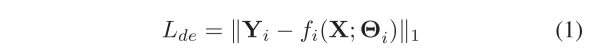
其中Θ_i表示网络参数。类似地，我们可以推导出自我监督网络的损失值L_SE：

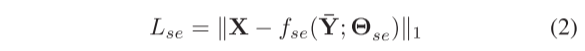
其中f_se是自监督网络学习的映射函数，Θ_se是网络参数，Y-是通过连接分解网络的m个输出得出的。最终损失值L是这两种损失值的组合：

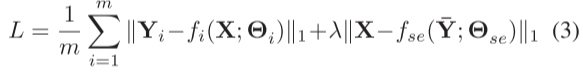
其中λ是用于平衡不同损失的正则化参数。在本文中，λ被经验地设定为0.0005。在训练阶段，每个样本都会产生一个损失值，并利用整个训练集的平均值来优化网络参数。