pytorch 笔记：GRU

1 介绍

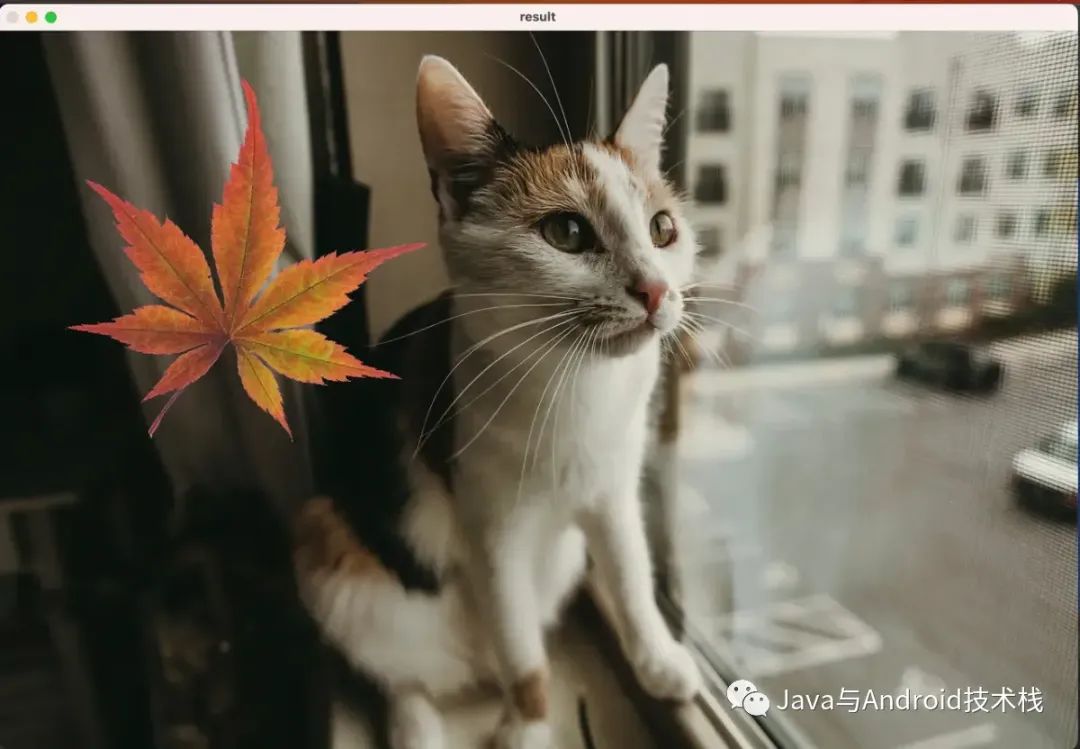
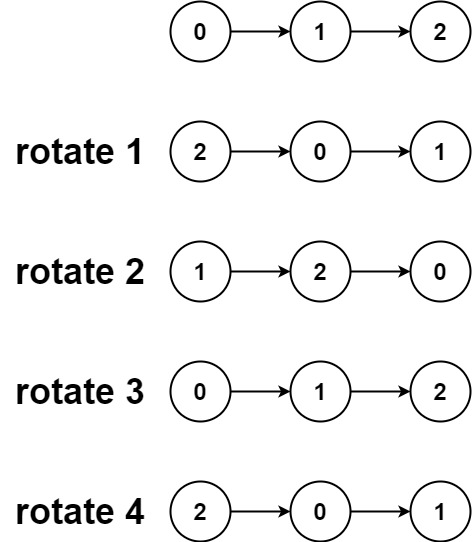
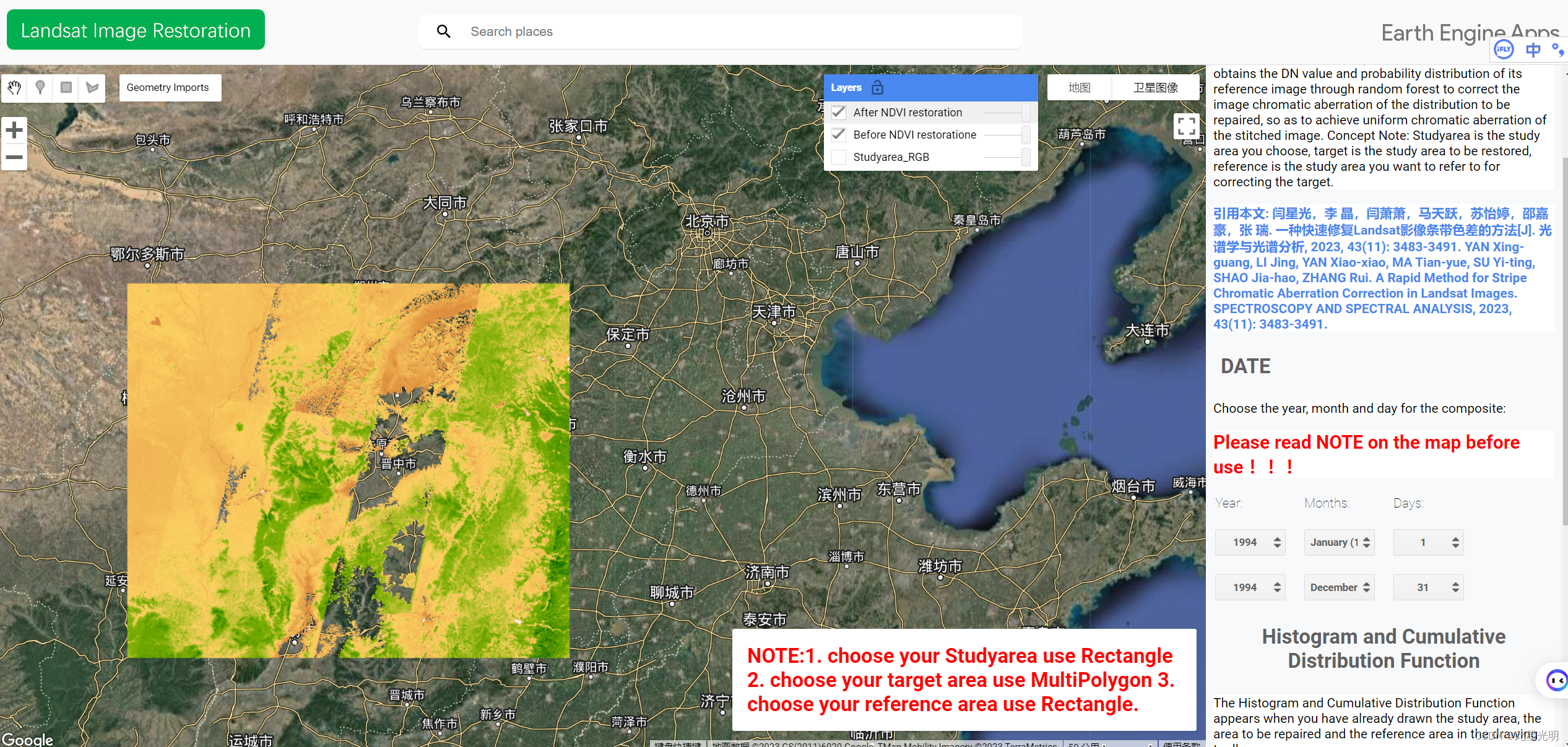
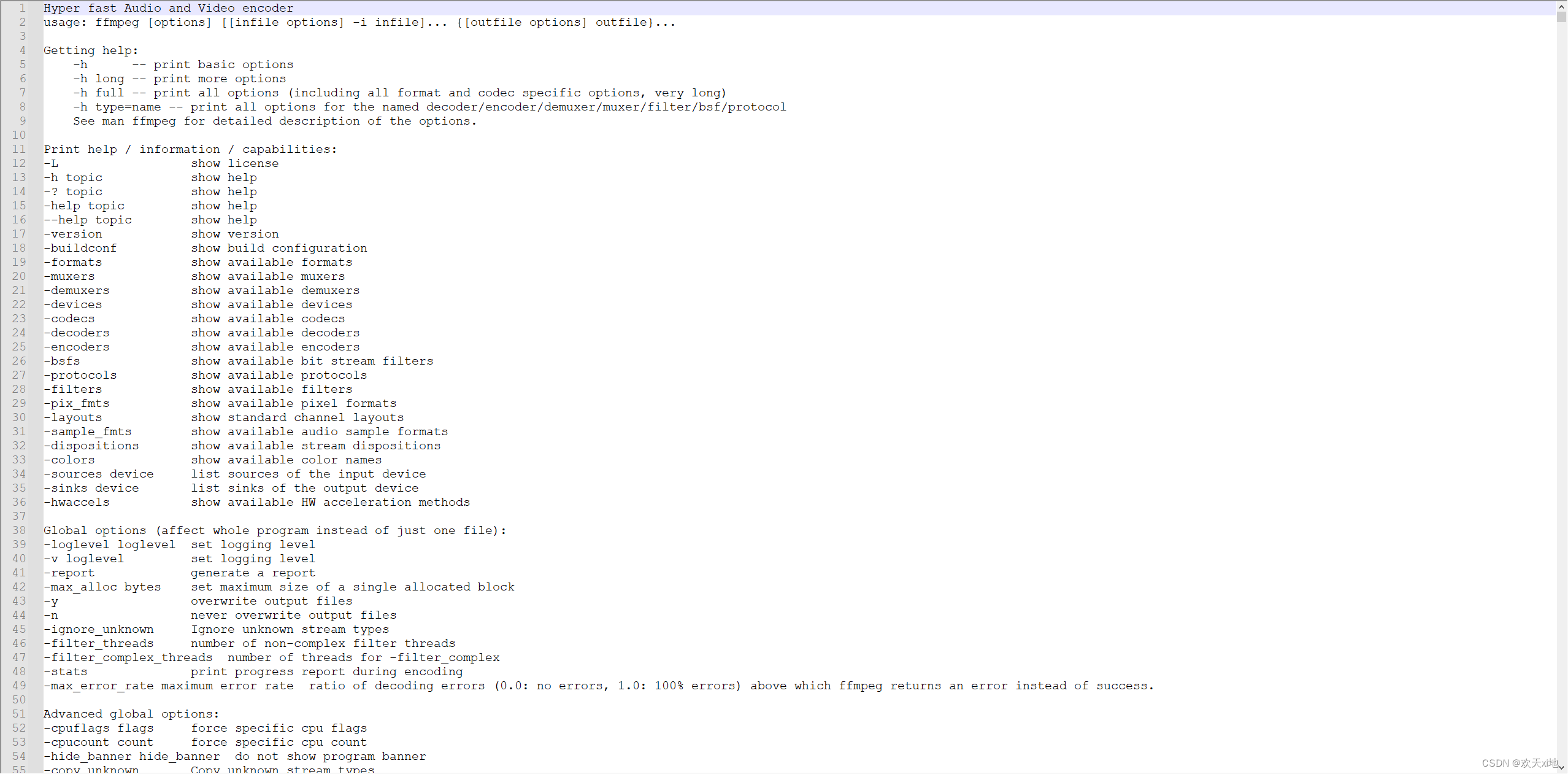
对于输入序列中的每个元素，每一层都计算以下函数：

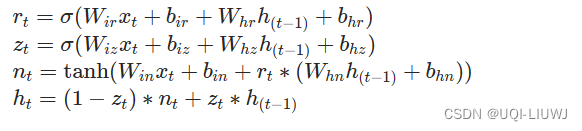
ht 是t时刻的隐藏状态
xt 是t时刻的输入
ht−1 是 t-1时刻同层的隐藏状态或 0时刻的初始隐藏状态
rt,zt,nt 分别是重置门、更新门和新门。
σ 是 sigmoid 函数
∗ 是 Hadamard 乘积。

在多层GRU中，第 l 层的输入 $x_t^{(l)}$ （对于 l≥2）是前一层的隐藏状态 $h_t^{(l-1)}$ 乘以概率 dropout $\delta_t^{t-1}$ 。

2 基本使用方法

torch.nn.GRU(self, input_size, hidden_size, num_layers=1, bias=True, batch_first=False, dropout=0.0, bidirectional=False,    device=None, dtype=None)

3 参数说明

input_size	输入 x 中预期的特征数
hidden_size	隐藏状态 h 的特征数
num_layers	GRU层数
bias	如果为 False，则该层不使用偏置权重bi,bh
batch_first	如果为 True，则输入和输出张量以（batch, seq, feature）提供，而不是（seq, batch, feature）
dropout	如果非零，则在除最后一层之外的每个 GRU 层的输出上引入一个 Dropout 层，其中 dropout 概率等于 dropout
bidirectional	如果为 True，成为双向 GRU。默认值为 False

输入：input (seq_len,batch,input_size), h_0(D*num_layers,batch,hidden_size) D表示单向还是双向GRU

输出：output（seq_len,D*hidden_size),h_n(D*num_layers,batch,hidden_size)

4 举例

import torch.nn as nnrnn = nn.GRU(input_size=5,hidden_size=10,num_layers=2)input_x = torch.randn(7, 3, 5)
#seq_len,batch,input_sizeh0 = torch.randn(2, 3, 10)
#D*num_layer,batch,hidden_sizeoutput, hn = rnn(input_x, h0)
output.shape, hn.shape,output, hn
#seq_len,batch,input_size D*num_layer,batch,hidden_size
'''
(torch.Size([7, 3, 10]),torch.Size([2, 3, 10]),tensor([[[ 2.3096e-01,  4.7877e-01, -6.0747e-02,  3.1251e-01,  4.4528e-01,-2.6670e-01, -1.1168e+00,  7.3444e-01, -8.5343e-01, -8.6078e-02],[ 1.4765e+00, -4.4738e-01,  2.9812e-01, -6.6684e-01,  4.5928e-01,1.5543e+00, -2.7558e-01, -7.5153e-01,  5.0880e-01,  6.0543e-02],[ 8.9311e-01,  4.0004e-01,  1.6901e-01,  1.5932e-01, -1.2210e-01,3.0321e-01, -2.8612e-01, -1.4686e-01,  2.8579e-01,  1.1582e-02]],[[ 3.2400e-01,  4.1382e-01, -1.6979e-01,  9.6827e-02,  4.6004e-01,-4.7673e-02, -5.0143e-01,  4.6305e-01, -6.7894e-01,  8.7199e-04],[ 1.0779e+00, -1.7995e-02,  1.4842e-01, -4.0097e-01,  2.1145e-01,1.0362e+00, -3.9766e-01, -5.6097e-01,  3.0160e-01,  1.4931e-02],[ 6.1099e-01,  3.5822e-01,  9.1912e-02, -6.6886e-02,  8.1180e-02,2.2922e-01, -1.2506e-01,  2.9601e-02,  2.8049e-02, -1.5160e-02]],[[ 3.4037e-01,  3.0256e-01, -9.5463e-02, -1.0667e-01,  4.1159e-01,-1.7158e-02, -1.6656e-01,  3.3041e-01, -4.9750e-01, -9.4554e-02],[ 7.2198e-01,  1.1721e-01,  5.7578e-02, -1.4264e-01,  4.4159e-02,7.4929e-01, -2.6565e-01, -3.7547e-01,  1.3828e-01,  6.9896e-02],[ 4.5888e-01,  2.9849e-01,  1.1400e-01, -1.4953e-01,  1.8319e-01,1.2005e-01, -1.0588e-01,  1.2678e-01, -9.6599e-02, -6.3649e-02]],[[ 2.6923e-01,  1.9539e-01, -8.3442e-02, -1.0092e-01,  2.9727e-01,5.5752e-02, -1.6502e-01,  1.5522e-01, -3.3283e-01, -1.5289e-02],[ 5.0674e-01,  2.2620e-01, -1.6900e-02, -1.6849e-02,  1.3829e-01,3.0847e-01, -1.6965e-01, -1.9627e-01,  3.3316e-02,  6.3073e-02],[ 3.9663e-01,  3.0165e-01, -1.2318e-02, -1.4176e-01,  2.3552e-01,-3.8588e-02, -8.2455e-03,  1.6961e-01, -1.3624e-01, -7.3225e-03]],[[ 2.4548e-01,  1.7003e-01, -1.9854e-01, -4.2608e-02,  2.2749e-01,6.0757e-02, -7.5942e-02,  1.0205e-01, -2.2418e-01,  1.1453e-01],[ 3.5747e-01,  1.6106e-01, -2.9625e-02,  7.5182e-02,  7.6844e-02,2.4100e-01, -7.6047e-02, -6.7489e-02, -3.3757e-02,  1.1799e-01],[ 3.1698e-01,  1.8008e-01, -5.1838e-02, -9.3295e-02,  1.7627e-01,2.4971e-02, -2.4372e-02,  1.4522e-01, -1.1888e-01,  3.5780e-02]],[[ 1.8998e-01,  9.6675e-02, -9.7632e-02, -8.5483e-02,  1.2471e-01,1.4351e-01, -3.0885e-02,  1.0894e-01, -1.8797e-01,  3.5201e-02],[ 2.8278e-01,  1.7304e-01, -1.9512e-02,  7.8874e-02,  1.4434e-01,1.0537e-01, -8.5619e-02,  2.5765e-02, -9.0284e-02,  9.8876e-02],[ 2.3387e-01,  8.8567e-02, -3.5850e-02, -2.8561e-02,  1.2145e-01,1.1404e-01, -1.1314e-01,  7.1272e-02, -1.0356e-01,  7.2997e-02]],[[ 1.5414e-01,  8.1896e-02, -1.4372e-01, -4.9761e-02,  8.5839e-02,1.7213e-01, -3.9533e-02,  4.7469e-02, -1.3332e-01,  8.3625e-02],[ 2.3274e-01,  1.5516e-01, -4.0695e-02,  3.1735e-02,  1.9340e-01,4.3769e-03, -4.9590e-02,  6.0317e-02, -1.0783e-01,  4.7750e-02],[ 1.3002e-01,  1.2265e-02, -3.3010e-03,  2.6260e-02,  6.5244e-02,2.3599e-01, -2.3918e-01, -4.4371e-02, -9.0464e-02,  1.1589e-01]]],grad_fn=<StackBackward0>),tensor([[[ 0.4118, -0.0513, -0.2540, -0.2115, -0.4503,  0.0357, -0.2615,-0.2243,  0.0580, -0.1405],[ 0.2653,  0.5365, -0.5024, -0.3466, -0.1986,  0.2726, -0.1399,-0.1821, -0.3203,  0.1749],[ 0.6847, -0.2840, -0.1549,  0.3359, -0.0230, -0.0229, -0.2775,-0.1442, -0.1158, -0.2203]],[[ 0.1541,  0.0819, -0.1437, -0.0498,  0.0858,  0.1721, -0.0395,0.0475, -0.1333,  0.0836],[ 0.2327,  0.1552, -0.0407,  0.0317,  0.1934,  0.0044, -0.0496,0.0603, -0.1078,  0.0477],[ 0.1300,  0.0123, -0.0033,  0.0263,  0.0652,  0.2360, -0.2392,-0.0444, -0.0905,  0.1159]]], grad_fn=<StackBackward0>))
'''

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.rhkb.cn/news/178801.html

如若内容造成侵权/违法违规/事实不符，请联系长河编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！