目录
1. 排序
1.1 冒泡排序的改进
2. 二叉树
2.1 二叉树的性质
3. 栈 & 队列
3.1 循环队列
3.2 链式队列
4. 平衡二叉搜索树——AVL树、红黑树
5 优先级队列(堆)
1. 排序
1.1 冒泡排序的改进
下面的排序方法中,关键字比较次数与记录的初始排列无关的是______。
A. 希尔排序
B. 冒泡排序
C. 直接插入排序
D. 直接选择排序
答案:D
基础的冒泡排序是与初始排列无关的,但是改进的冒泡排序,当一趟排序之后没有交换,则说明序列已经有序,则可退出排序,例如一个已经排好序的序列,第一次循环之后就可以退出排序了;
所以说对比B选项和D选项,D选项肯定时最优解
2. 二叉树
2.1 二叉树的性质
① 对于任意一颗二叉树,设叶子节点个数为n0,度为二的节点的个数为n2,则满足n0 = n2 + 1
某二叉树共有 399 个结点,其中有 199 个度为 2 的结点,则该二叉树中的叶子结点数为() A. 不存在这样的二叉树
B. 200
C. 198(错误)
D. 199
答案:B
②深度
根节点的深度为0
③ 完全二叉树每一层的节点个数
一棵完全二叉树第六层有9个叶结点(根为第一层),则结点个数最多有()
A. 112
B. 111
C. 107
D. 109 (2^6-1 + 2^(7-1)-9*2 = 109)
答案:D :第六层满节点,题目要求第六层有9个叶子节点,则需要第六层的9个节点不挂叶子节点,所以第七层节点有2^(7-1)-9*2个节点
1. 满二叉树第i层节点个数:2^(i-1);
2. 总共i层的满二叉树所有节点个数:2^i - 1
3. 队列
3.1 循环队列
现有一循环队列,其队头指针为front,队尾指针为rear;循环队列长度为N。其队内有效长度为()(“左闭右开”)
A. (rear - front + N) % N + 1(错误)
B. (rear - front + N) % N
C. (rear - front) % (N + 1)
D. (rear - front + N) % (N - 1)
答案:B

3.2 链式队列
用不带头结点的单链表存储队列,其队头指针指向队头结点,队尾指针指向队尾结点,则在进行出队操作时()
A. 仅修改队头指针(错误)
B. 仅修改队尾指针
C. 队头、队尾指针都可能要修改
D. 队头、队尾指针都要修改
答案:C
※当队列只有一个节点时,出队列对头队尾指针均需要修改、
4. 栈
4.1 运算表达式
表达式3*2^(4+2*2-6*3)-5求值过程中当扫描到6时,对象栈和运算符栈为(),其中^为乘幂
A. 3,2,4,1,1;(*^(+*-
B. 3,2,8;(*^-(错误)
C. 3,2,4,2,2;(*^(-
D. 3,2,8;*^(-
答案:D
数据栈:有数据就直接入栈
运算符栈:设遍历到当前的运算符位x,如果栈不为空,比较栈顶与当前运算符优先级x,当栈顶运算符优先级大于或者等于x的优先级,则出栈,并将两个数据栈的数据出栈,计算出对应的数据,加入到数据栈中,否则将运算符入栈
/*根据上述原理模拟实现一个计算器*/
#include <iostream>
#include <unordered_map>
#include <stack>
#include <functional>
#include <string>#define MAX_PRI INT_MAXusing namespace std;
int main() {//数据栈stack<double> _data; //运算符栈stack<char> _operator; //运算符优先级unordered_map<char, int> pri{ {'+', 0}, {'-', 0}, {'*', 1}, {'/', 1}, {'^', 2}, {'(', MAX_PRI }, {')', MAX_PRI}};unordered_map<char, function<double(double, double)>> func{{'+', [](double x, double y) -> double { return x + y; }},{'-', [](double x, double y) -> double { return x - y; }}, {'*', [](double x, double y) -> double { return x * y; }},{'/', [](double x, double y) -> double { return x / y; }},{'^', [](double x, double y) -> double { return pow(x, y); }}};string exp;cin >> exp;auto calculate = [&_data, &_operator, &func]() {char op = _operator.top();_operator.pop();double x = _data.top();_data.pop();double y = _data.top();_data.pop();_data.push(func[op](y, x)); //运算顺序与出栈顺序相反};auto stringtonum = [&exp, &pri](int& i) -> double {int j = i + 1;while (j < exp.length() && pri.find(exp[j]) == pri.end()) j++;double num = stod(exp.substr(i, j - i));i = j - 1; return num;};for (int i = 0; i < exp.length(); ++i) {char e = exp[i];if (pri.find(e) == pri.end()) { //当前字符不是运算符,则切割数字_data.push(stringtonum(i));} else if (e == '(') {_operator.push('(');} else if (e == ')') {while (_operator.top() != '(') {calculate();}_operator.pop();} else {//当前运算符优先级<=栈顶运算符优先级,则出栈计算while (!_operator.empty() && pri[_operator.top()] >= pri[e] && _operator.top() != '(') {calculate();}_operator.push(e);}}while (!_operator.empty()) {calculate();}cout << _data.top() << endl;
}5. 平衡二叉搜索树——AVL树、红黑树
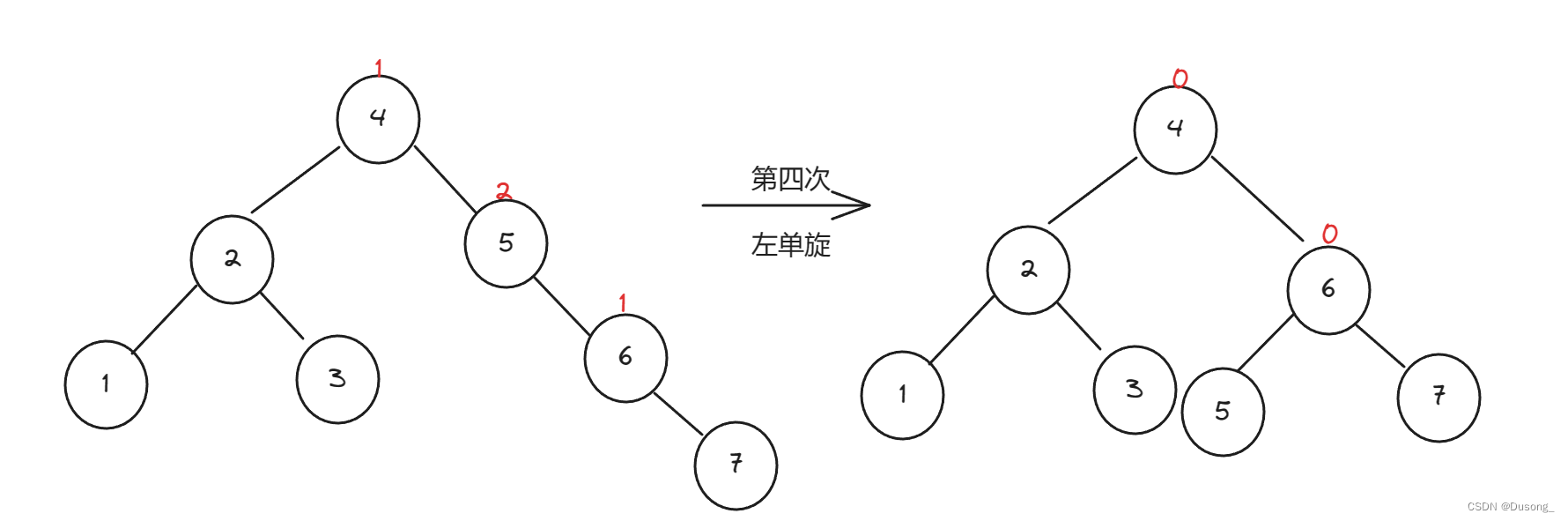
若将关键字1,2,3,4,5,6,7 依次插入到初始为空的平衡二叉树 T 中,则 T 中平衡因子为 0 的分支结点的个数是( )
A. 0
B. 1
C. 2
D. 3
答案:D (分支节点:不包含叶子节点)



6. 优先级队列(堆)
下述二叉树中,哪一种满足性质:从任一结点出发到根的路径上所经过的结点序列按其关键字有序()
A. 二叉排序树(错误)
B. 哈夫曼树
C. AVL树
D. 堆
答案:D
知识点:小根堆与大根堆(详细看数据结构一、1.2节)
7. 哈希表
采用哈希表组织100万条记录,以支持字段A快速查找,则()
A. 理论上可以在常数时间内找到特定记录(错误:发生哈希冲突)
B. 所有记录必须存在内存中
C. 拉链式哈希曼最坏查找时间复杂度是O(n)
D. 哈希函数的选择跟A无关
答案:C