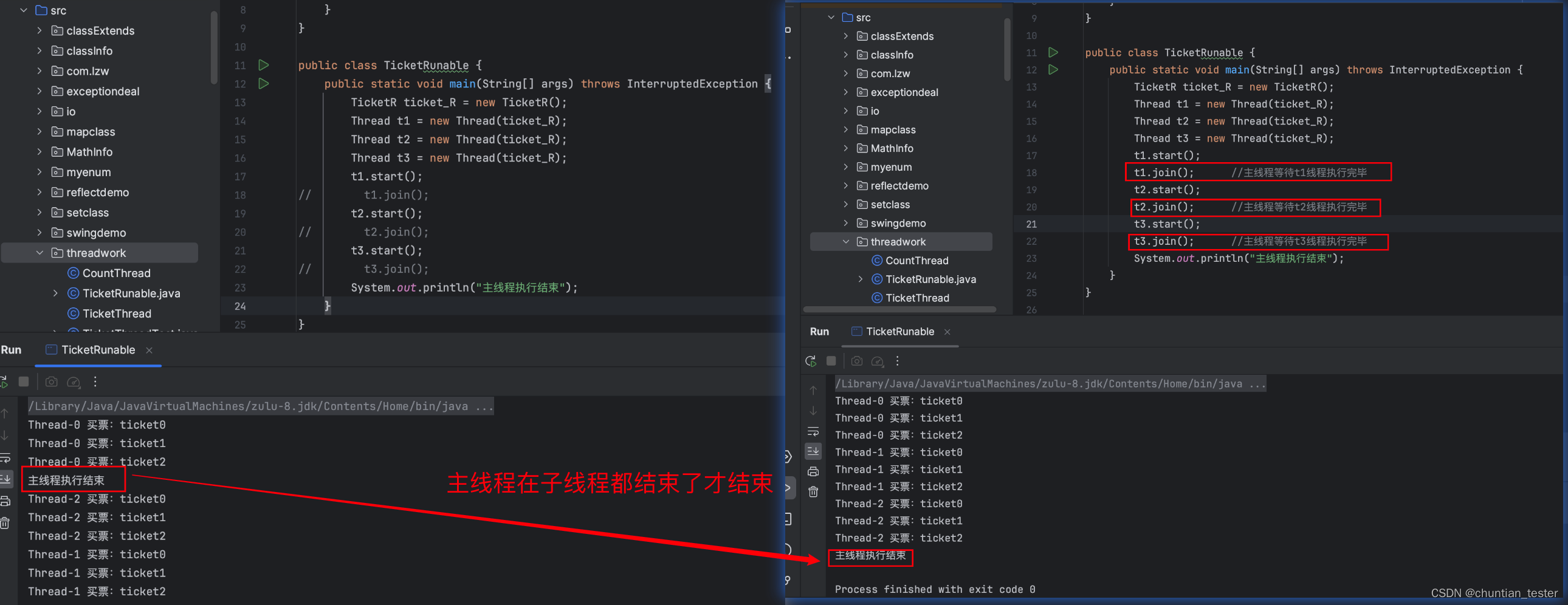
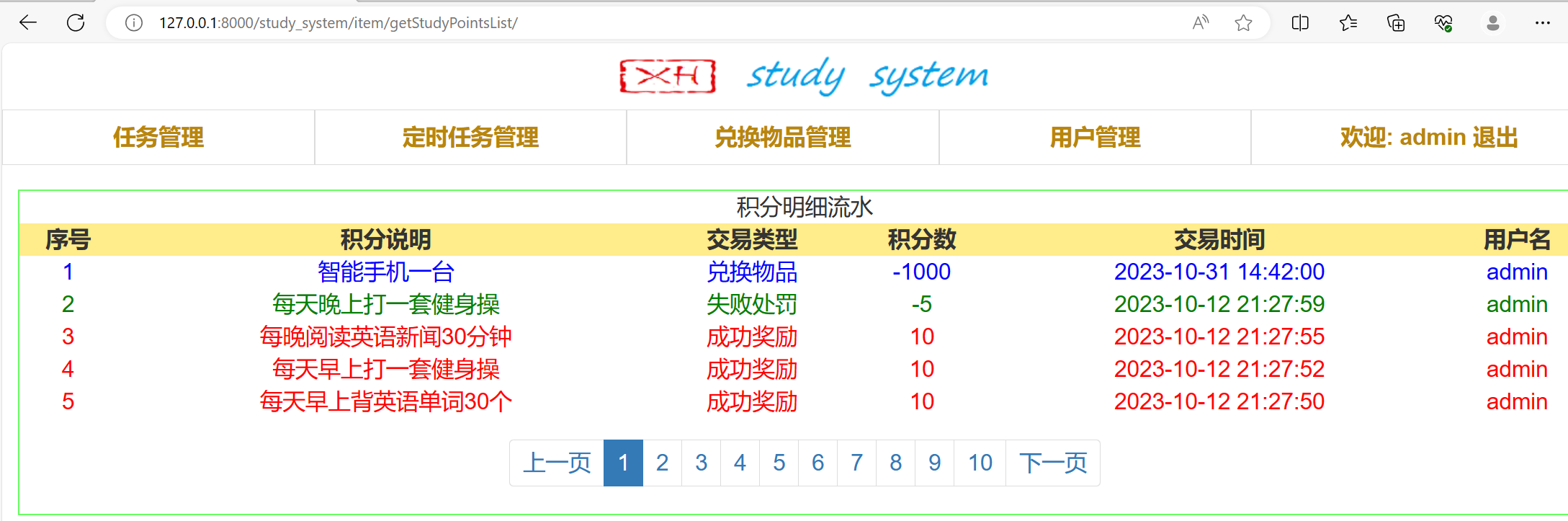
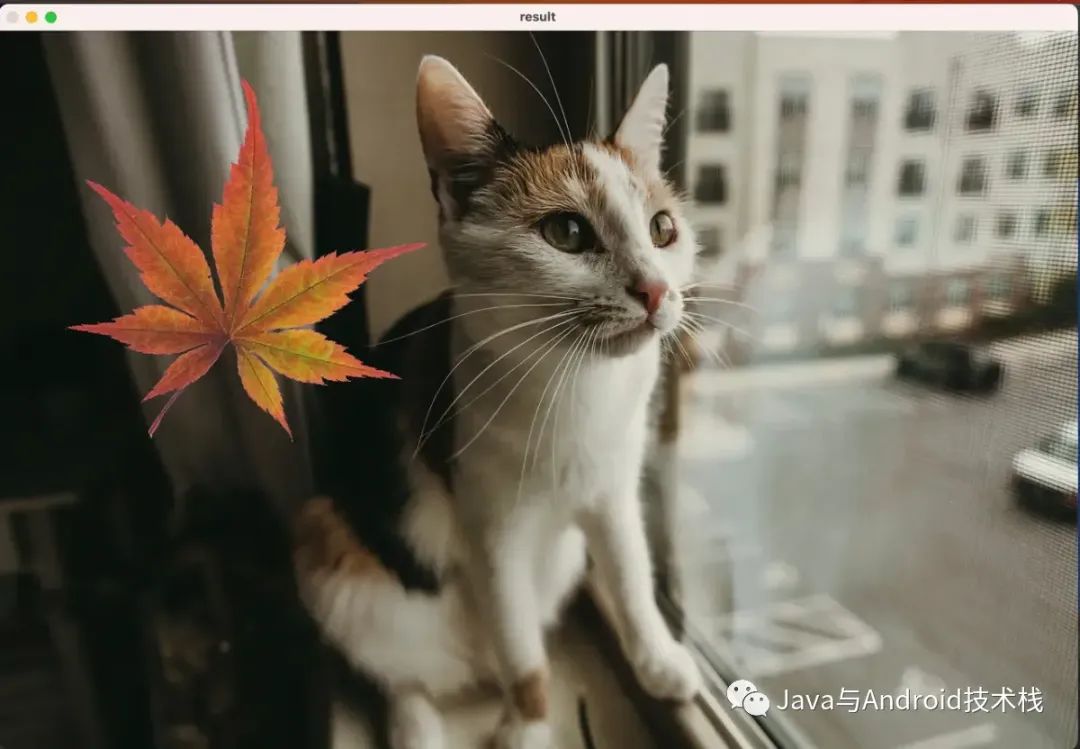
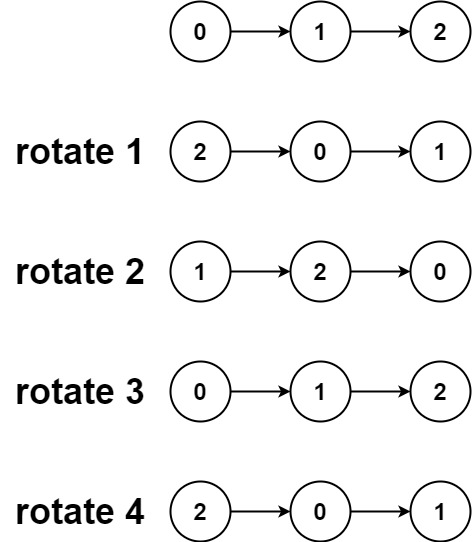
交流通路实质
列出电路方程1,方程1对时刻t做微分 所得方程1‘ 即为 交流通路
方程1对时刻t做微分:两个不同时刻的方程1相减,并 令两时刻差为
无穷小
微分 改成 差
模电学习路径:
理论
《电路原理》清华大学 于歆杰 朱桂萍 陆文娟
电路原理-清华大学-于歆杰 朱桂萍 陆文娟-在线-低清(1.97 GB) (完整,但不清晰)
130*0402百度网盘
《电路原理》清华大学 于歆杰 朱桂萍 陆文娟 - 在线教学 - 高清视频- YouTube (只有前13讲,但清晰)
https://www.youtube.com/playlist?list=PLfn0svxxDodh3-2SLLuTnL4Clqjbx5yuj
赵建勋 : 模电理论分析、高频电路理论分析
https://www.icourse163.org/u/mooc1489367363074?userId=1025046621
模拟电子电路与技术基础 赵建勋
https://www.icourse163.org/learn/XDU-1001960018?tid=1002057049#/learn/content?type=detail&id=1002793163&cid=1003150874
工程高频通信电路基础 赵建勋
https://www.icourse163.org/learn/XDU-1206395808?tid=1465860461#/learn/content?type=detail&id=1245804279&cid=1271012738
例子
找 multisim 实际电路例子 (其元件有合适的取值),
用上面学会的理论 去分析这些例子
焊接芯片记录
stm32f103c6t6a qfp48 最小系统板,自制的
- 尖头烙铁 390摄氏度 焊接外围元件
- 尖头烙铁 290摄氏度 焊接 stm32f103c6t6a qfp48 ,每次焊接时长5到10秒后 离开芯片 (防止芯片烧坏), 最终最小系统板正常工作 说明 这样的温度和每次焊接时长 芯片不会坏。
STM32复位电路、电容阻力理解0
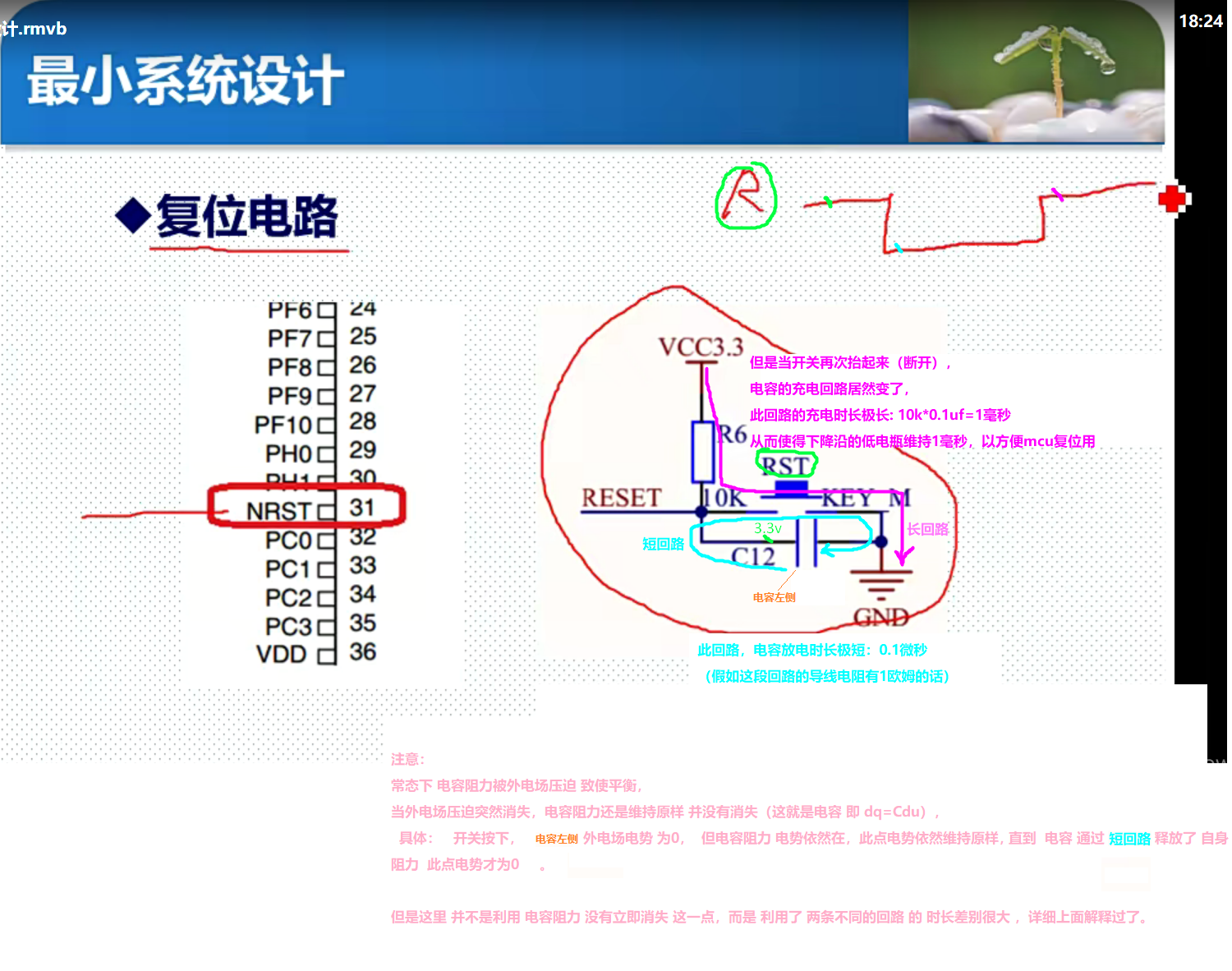
图来源