文章目录
- 前言
- 回溯的核心问题
- 撤销操作解释
- 总结
前言
提示:阳光好的时候,会感觉还可以活很久,甚至可以活出喜悦。 --余秀华
回溯是非常重要的算法思想之一,主要解决一些暴力枚举也搞不定的问题(这里埋个坑💣)例如组合、分割、子集、棋盘等等。从性能角度来看回溯算法的效率并不是很高,但是对于暴力也解决不了的问题,它往往很快可以出结果,效率低就可以理解了吧。接下来,就看看回溯的事情吧🤩
回溯的核心问题
递归+局部枚举+放下前任
接着看这个题目:77. 组合 - 力扣(LeetCode)

当n = 4时,我们可以选择的有n有{1,2,3,4}这四种情况,所以我们从第一层到第二层的分支有四个,分别表示可取1,2,3,4.而且这里从左到右取数,取过的数,不在重复取。第一次取1,集合变为2,3,4.因为k= 2,我们也只能再取1个数就可以了,分别取2,3,4.得到的集合就是[1,2]、[1,3]、[1,4]。一次类推:
横向:
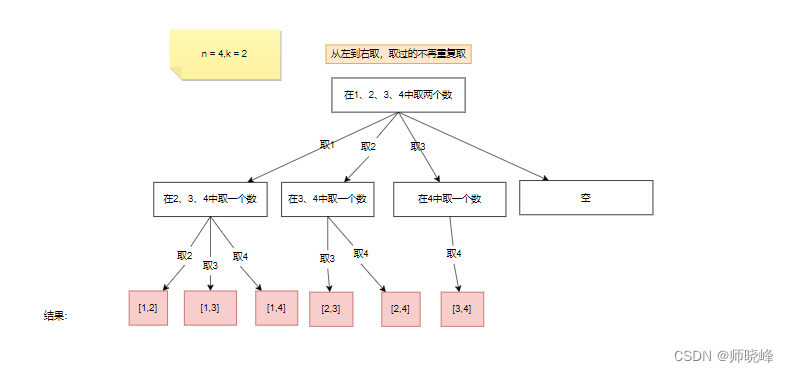
每次从集合中选取元素,可选择的范围回逐步收缩,到了取4时就直接返为空了。
继续观察树结构,可以发现,图中每次访问到一个叶子节点(图中的标记处),我们就可以得到一个结果。虽然到最后时空的,但是不影响最终结果。这里相当于从根节点开始每次选择的内容(分支)达到叶子节点时,将其收起起来就是我们想要的结果。
你可以尝试画下n=5,k=3的结果:有没有感觉
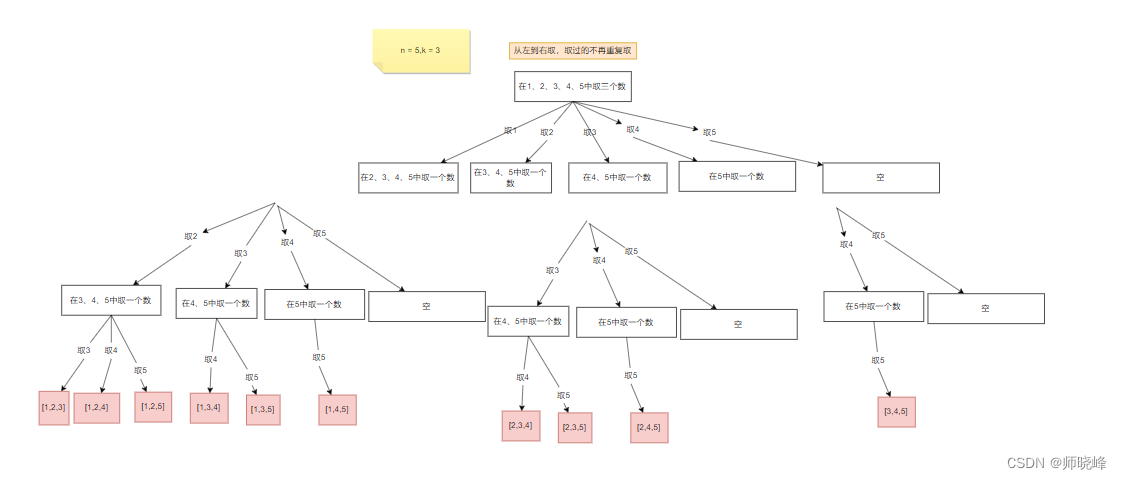
从图中我们发现元素个数n相当于树的宽度(横向),而每个结果的元素个数k相当于树的深度(纵向)。所以我们说回溯问题就是一纵一横而已。在分析我们回发现下面几个规律:
- 我们每次选择都是从类似{1,2,3,4},{1,2,3,4}这个样的序列中一个一个选的,这就是为什么说是局部枚举,后面的枚举范围回越来越小。
- 枚举时,我们就是简单的暴露测试而已,一个一个验证,能否满足要求,从上图可以看到,这就是N叉树的遍历过程,一次代码相似度很高。
- 我们再看叶子过程,这部分是不是和(n = 4,k = 2)处理的结果一致,也就说是很明显的递归结构。
到此,我们还有一个问题待解决,就是回溯一般会有一个手动撤销的操作,为什么要这么做呢?
继续观察纵横图:
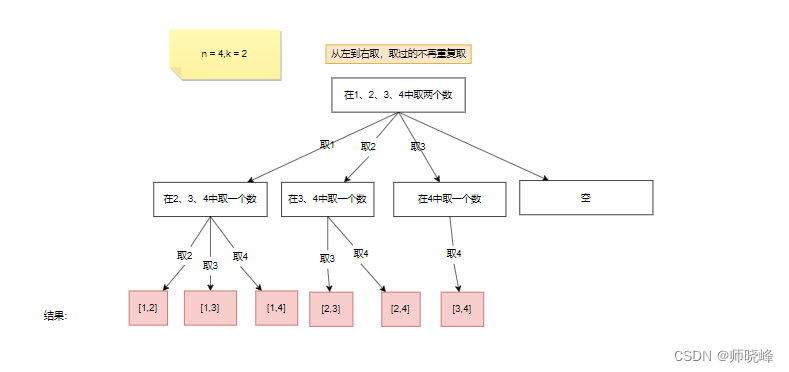
我们可以看到,我们收集的每个结果不是针对叶子节点的,而是针对树枝的,比如最上层我们首先确定了1,下层我们如果选择了2,那么结果就是{1,2},如果选择了3,结果就是{1,3}.一次类推。现在时怎么确定得到第一个结果时{1,2}之后,得到第二个结果是{1,3}呢?
继续观察纵横图 ,可以看到,我们在得到{1,2}之后将2撤销,再继续使用3,就得到了{1,3},同理也可以得到{1,4},之后这一层就没有了,我们可以撤销1,继续从最上层取2继续进行。
这里对应的代码操作就是先将第一个结果放在临时列表的Path里面,得到第一个结果{1,2},之后就将path里面的内容放进结果列表resultList中,之后,将path里面的2撤销掉,继续寻找下一个结果{1,3},继续将path加入resultList中,然后再次撤销,继续寻找。
现在了解为什么要撤销,看图。这个过程,我们称它“放下前任,继续前进”,后面的回溯大都是这样的思路。
这几条就是回溯的基本规律,了解这一点,我们就可以看看代码是怎么回事了,到此我们看看完整的代码时怎样的:
public List<List<Integer>> combine(int n, int k) {List<List<Integer>> res = new ArrayList<>();if (k <=0 || n < k){return res;}
Deque<Integer> path = new ArrayDeque<>();
dfs(n,k,1,path,res);return res;}
public void dfs(int n,int k,int startIndex,Deque<Integer> path,List<List<Integer>> res){// 递归终止条件,path 等于k(刚好完成一次if (path.size() == k){res.add((new ArrayList<>(path)));return;}// 针对每个节点,这里就是遍历搜索,也就是枚举for(int i = startIndex; i <= n; i++){// 向路径里添加一个数(分支里的取值path.addLast(i);// 搜索起点要加1,就是缩小范围,准备下一轮递归(这里不允许重复dfs(n,k,i + 1,path,res);// 递归之后要做同样的逆向操作,撤销掉path.removeLast();}}
上面代码还有一个问题需要解释:startIndex和i是怎么变化的,为什么要传递到下一层(+ 1)
我们来看看这里的递归循环:
// 针对每个节点,这里就是遍历搜索,也就是枚举for(int i = startIndex; i <= n; i++){// 向路径里添加一个数(分支里的取值path.addLast(i);// 搜索起点要加1,就是缩小范围,准备下一轮递归(这里不允许重复dfs(n,k,i + 1,path,res);// 递归之后要做同样的逆向操作,撤销掉path.removeLast();}
这里的循环有什么作用呢?看看这里,其实来说是一个枚举,第一次n=4,可以选择1,2,3,4四种情况,所以就存在4个分支,for就需要执行4次:
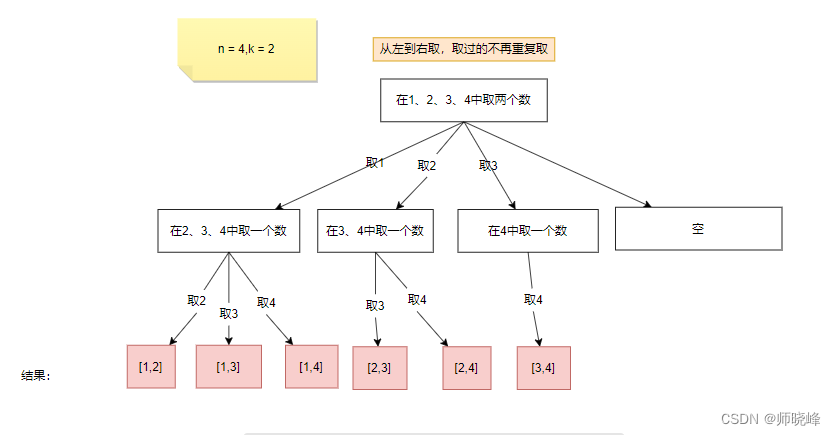
对于第二层来说,第一个数,选择1之后,身下的元素就只有2,3,4了。所以这时候for循环就执行3次,后面的只有2次和1次了。
撤销操作解释
如果你还是不清楚的话,这里就带图详细的走一遍,回溯也就是这个地方有点晕,拿下就是胜利✌。
// 针对每个节点,这里就是遍历搜索,也就是枚举for(int i = startIndex; i <= n; i++){// 向路径里添加一个数(分支里的取值path.addLast(i);// 搜索起点要加1,就是缩小范围,准备下一轮递归(这里不允许重复dfs(n,k,i + 1,path,res);// 递归之后要做同样的逆向操作,撤销掉path.removeLast();}
为什么要remove呢?看下图,当第一层取1时,最底层的遍历从左到右执行,取2,取3,取4.而取3的时候,此时res里面存储的是{1,2},所以这里前提是需要撤销掉2(path.removeLast();)的作用。
这里我们拆解一下递归方法,将递归拆分成函数调用,输出第一条路径{1,2}的步骤如下:
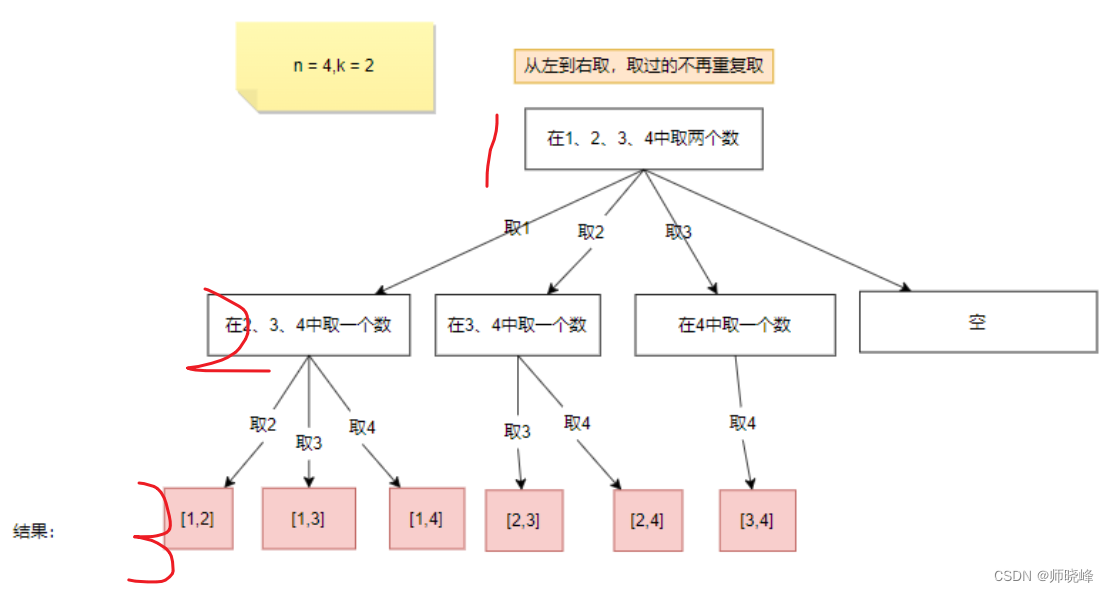
我们在递归说过一个特点:不到南墙不回头,回溯也是这个道理,我们看看这个过程。

然后,怎么在次进行呢,这里就需要撤回一下了,但是如果将这里的remove代码去掉,就会是这个样子:
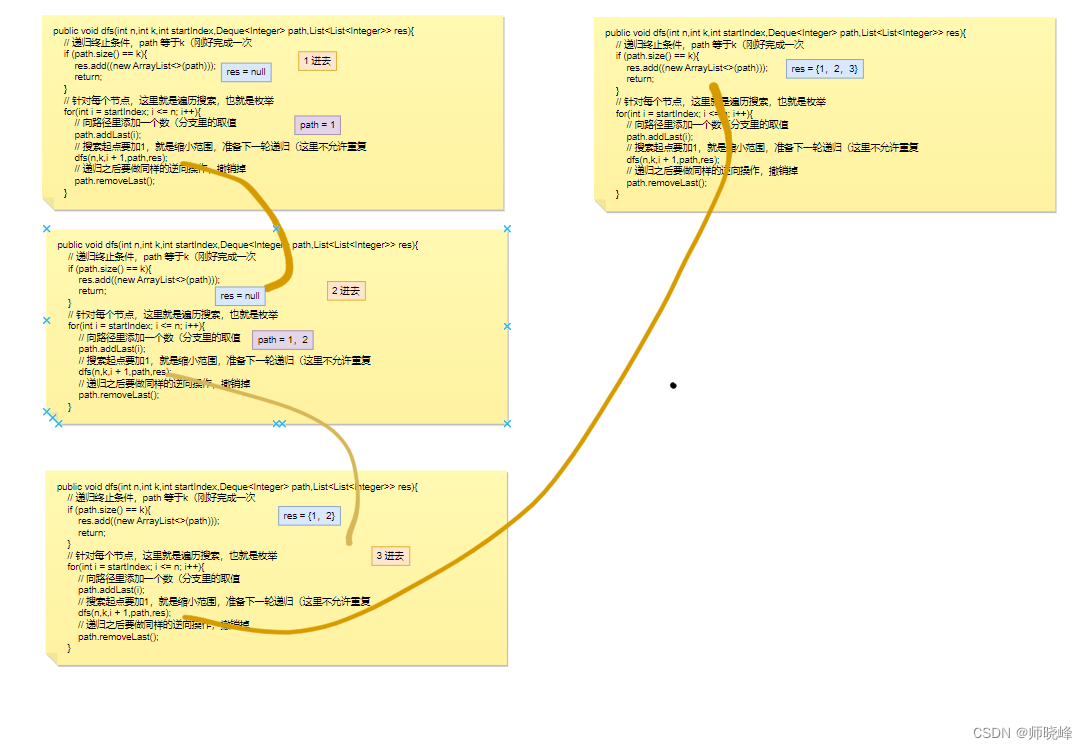
这里知道遍历完成,然会的就不做撤销,就会下一场进入for循环,也就是回变成{1,2,3}.
path是一个全局的引用的,各个递归的函数是公用的,所以这里处理完{1,2},之后,需要把2撤出去,将1保留,再让三进入,从而得到{1,3}.所以这里不许remove一下的。
同样处理完之后,后续的也是依次处理,需要撤销的,这里也就是不得不处理撤销的操作。
总结
提示:什么叫回溯;保留状态;撤销操作;回溯核心思想;回溯的入门
如果有帮助到你,请给题解点个赞和收藏,让更多的人看到 ~ ("▔□▔)/
如有不理解的地方,欢迎你在评论区给我留言,我都会逐一回复 ~
也欢迎你 关注我 ,喜欢交朋友,喜欢一起探讨问题。