别怕，卷积其实很简单

原文地址：https://blog.csdn.net/qq_39521554/article/details/79083864

相信很多时候，当我们在看到“卷积”时，总是处于一脸懵逼的状态，不但因为它的本义概念比较难理解，还因为它在不同的应用中发挥出的变幻莫测的作用也时常让人迷糊。但这些应用其实本质上都是同一种东西，理解了卷积的来源，就可以举一反三。其实我个人对于卷积的理解，很长时间都处于似懂非懂的状态，就像傅里叶变换的一些tricky points，只求在应用中不出差错，不求甚解。但是如果想要真正做好learning的东西，我认为在真正的学习理论基础前，必须将概念的本质搞清楚。因此，这篇文章便是为工科，理科以及其他领域对此感兴趣的同学而整理，内容简易通俗，便于理解。

什么是卷积

卷积，很多时候都是我们在各种工程领域，信号领域所看到的常用名词，比如系统

通俗易懂的说，就是

输出 = 输入 * 系统

虽然它看起来只是个复杂的数学公式，但是却有着重要的物理意义，因为自然界这样的系统无处不在，计算一个系统的输出最好的方法就是运用卷积。更一般的，我们还有很多其他领域的应用：

统计学中，加权的滑动平均是一种卷积。

概率论中，两个统计独立变量X与Y的和的概率密度函数是X与Y的概率密度函数的卷积。

声学中，回声可以用源声与一个反映各种反射效应的函数的卷积表示。

电子工程与信号处理中，任一个线性系统的输出都可以通过将输入信号与系统函数（系统的冲激响应）做卷积获得。

物理学中，任何一个线性系统（符合叠加原理）都存在卷积。

计算机科学中，卷积神经网络（CNN）是深度学习算法中的一种，近年来被广泛用到模式识别、图像处理等领域中。

这6个领域中，卷积起到了至关重要的作用。在面对一些复杂情况时，作为一种强有力的处理方法，卷积给出了简单却有效的输出。对于机器学习领域，尤其是深度学习，最著名的CNN卷积神经网络(Convolutional Neural Network, CNN)，在图像领域取得了非常好的实际效果，始一出现便横扫各类算法。

那么，到底什么是卷积呢？

首先给大家一个果壳上关于卷积的著名暴力讲解：

比如说你的老板命令你干活，你却到楼下打台球去了，后来被老板发现，他非常气愤，扇了你一巴掌（注意，这就是输入信号，脉冲），于是你的脸上会渐渐地（贱贱地）鼓起来一个包，你的脸就是一个系统，而鼓起来的包就是你的脸对巴掌的响应，好，这样就和信号系统建立起来意义对应的联系。

下面还需要一些假设来保证论证的严谨：假定你的脸是线性时不变系统，也就是说，无论什么时候老板打你一巴掌，打在你脸的同一位置（这似乎要求你的脸足够光滑，如果你说你长了很多青春痘，甚至整个脸皮处处连续处处不可导，那难度太大了，我就无话可说了哈哈），你的脸上总是会在相同的时间间隔内鼓起来一个相同高度的包来，并且假定以鼓起来的包的大小作为系统输出。好了，那么，下面可以进入核心内容——卷积了！

如果你每天都到地下去打台球，那么老板每天都要扇你一巴掌，不过当老板打你一巴掌后，你5分钟就消肿了，所以时间长了，你甚至就适应这种生活了……如果有一天，老板忍无可忍，以0.5秒的间隔开始不间断的扇你的过程，这样问题就来了，第一次扇你鼓起来的包还没消肿，第二个巴掌就来了，你脸上的包就可能鼓起来两倍高，老板不断扇你，脉冲不断作用在你脸上，效果不断叠加了，这样这些效果就可以求和了，结果就是你脸上的包的高度随时间变化的一个函数了（注意理解）；

如果老板再狠一点，频率越来越高，以至于你都辨别不清时间间隔了，那么，求和就变成积分了。可以这样理解，在这个过程中的某一固定的时刻，你的脸上的包的鼓起程度和什么有关呢？和之前每次打你都有关！但是各次的贡献是不一样的，越早打的巴掌，贡献越小，所以这就是说，某一时刻的输出是之前很多次输入乘以各自的衰减系数之后的叠加而形成某一点的输出，然后再把不同时刻的输出点放在一起，形成一个函数，这就是卷积，卷积之后的函数就是你脸上的包的大小随时间变化的函数。

本来你的包几分钟就可以消肿，可是如果连续打，几个小时也消不了肿了，这难道不是一种平滑过程么？反映到剑桥大学的公式上，f(a)就是第a个巴掌，g(x-a)就是第a个巴掌在x时刻的作用程度，乘起来再叠加就ok了

通过这个通俗化的例子我们从基本概念上了解了卷积，那么更严格的定义是怎样的呢？

从数学上讲，卷积只不过是一种运算，对于很多没有学过信号处理，自动控制的同学来说各种专业的名词可以不做了解。我们接着继续：

本质上卷积是将二元函数 U(x,y) = f(x)g(y) 卷成一元函数 V(t) ，俗称降维打击。

怎么卷？

考虑到函数 f 和 g 应该地位平等，或者说变量 x 和 y 应该地位平等，一种可取的办法就是沿直线 x+y = t 卷起来：

$V(t) = \int_{x+y=t} U(x,y) \,\mathrm{d}x$

卷了有什么用？

可以用来做多位数乘法，比如：

$\begin{align}42 \times137 &= (2\times10^0+4\times10^1)(7\times10^0+3\times10^1+1\times10^2) \\&= (2\times7)\times10^0 + (2\times3+4\times7)\times10^1+(2\times1+4\times3)\times10^2 + (4\times1)\times10^3 \\&= 14 + 340+1400+4000 \\&= 5754\end{align}$

注意第二个等号右边每个括号里的系数构成的序列 (14,34,14,4)，实际上就是序列 (2,4) 和 (7,3,1) 的卷积

在乘数不大时这么干显得有点蛋疼，不过要计算很长很长的两个数乘积的话，这种处理方法就能派上用场了，因为你可以用快速傅立叶变换 FFT 来得到卷积，比示例里的硬乘要快。

这里有一个不太严格的理解：
$(\sum_{n=1}^{\infty}{a_nx^n})(\sum_{n=1}^{\infty}{b_nx^n})=\sum_{n=1}^{\infty}(\sum_{k=1}^{n}a_kb_{n-k})x^n$
$x^n$ 是“基”， $a_n$ 是在这个基上的展开系数。两个多项式乘积的在基上展开的系数就是两个多项式各自在基上展开系数的卷积。
$x^n$ 对应着频率不同的 $\exp(ikt)$ ，系数对应着其傅里叶变换。自然就是乘积的傅里叶变换等于傅里叶变换的卷积了。

卷积的内核（涉及推导过程，可以跳过）：

首先我们有这样一个概念：内积、积分、投影这三者其实从某个角度上讲是一个意思。

定义一组向量 $\alpha=(\alpha_{1},\alpha_{2},...,\alpha_{n})$ ，另一组向量 $\beta=(\beta_{1},\beta_{2},...,\beta_{n})$ ，那么内积可以表达为：

$\alpha \beta = \alpha_{1} \beta_{1}+\alpha_{2} \beta_{2}+...+\alpha_{n} \beta_{n}=\sum_{i=1}^{n}{\alpha_{i} \beta_{i}}$

这即是内积，也是累加（积分）。投影的概念则可以理解为向量a在基向量b上的一组投影，坐标为 $(\alpha_{1},\alpha_{2},...,\alpha_{n})$ ，这和一个点在3D欧几里得空间的三轴投影坐标是一个道理。

这样，先来看看Fourier变换在做什么：

$F(\omega)=\int_{-\infty }^{+\infty} f(t)e^{-j\omega t}dt$

再引入一个完美的式子，欧拉公式：

$e^{ix}=cosx+isinx$

从Fourier的定义式可以看出是对f(t)和 $e^{-j\omega t}$ 相乘后在无穷域上对其进行积分，那么其实就是将f(t)投影在 $e^{-j\omega t}$ 上，如果不理解 $e^{-j\omega t}$ 就变换为两个正交的三角函数（欧拉公式就在这里起作用）。所以这就明朗了：Fourier把f(t)投影到了两个为正交关系的正弦和余弦空间中。也可以从周期信号的Fourier级数分解表达式更容易看出这个投影关系。

看完Fourier再看来控制论领域的Laplace变换在做什么：

$F(s)=\int_{0}^{\infty}f(t)e^{-\sigma t}e^{-j\omega t}dt=\int_{0}^{\infty}f(t)e^{-st}dt$

首先，控制领域里面经常用到阶跃信号，不幸的是它不满足狄利克雷第三条件，因此它对Fourier变换免疫，所以聪明的Laplace用了一个衰减因子 $e^{-\sigma t}$ 将其进行衰减后再做Fourier变换。到了负无穷的区域这衰减因子可就成了递增因子，所以Laplace变换仅限于大于0的区域，对于小于0的区域用系统初始状态表达就好了。从这点角度上讲，Laplace变换相当于对 $f(t)e^{-\sigma t}$ 做了一个单边Fourier变换。

然后，分析方法同上，可以看到Laplace把f(t)投影到了 $e^{-st}$ 空间，这就是s平面。它比Fourier更厉害的地方是不仅可以看到虚轴上 $\omega$ 的成分，还可以在实轴上看到Fourier看不到的衰减因子 $\sigma$ 成分，这是Fourier做不到的。所以Laplace在Fourier的基础上把信号拓展到了衰减因子实轴上，这个衰减因子 $\sigma$ 和系统的阻尼 $\zeta$ ，自然震荡角频率 $\omega_{n}$ 密切相关，直接影响了系统的调节时间 $t_{s}$ 。学过自控原理的同学应该知道在频域章节，我们得到系统的频域响应曲线都是通过传递函数来直接转化的，公式就是s=jw。这也就是说Fourier活在一维虚轴空间，Laplace活在二维平面空间，想要得到一维空间上关于w的表达形式，只需要在s平面上做降维处理即可。

回过头来再来看看卷积投影：

$f(t)*g(t)=\int_{-\infty }^{+\infty}f(\tau)g(t-\tau)d\tau$

这个投影有点奇怪，它在投影之前先把 $g(\tau)$ 做了一个反对称，然后再投影。对应到前面推导的系统卷积表达式：

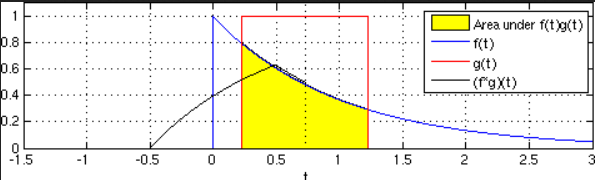
$r(t)*f(t)=\int_{-\infty }^{+\infty}f(\tau)r(t-\tau)d\tau$

相当于在投影之前，先把输入信号r(t)在时间轴上翻转了180°，然后与系统f(t)进行投影。投影的概念我们可以很好理解，无论是向量内积运算相当于线投影，或者空间的一个多面体在三维空间平面上的投影面，这种投影运算就相当于一种重合面积。如果从这个角度去看输入、系统和输出三者之间的关系，那么就可以从图形角度去理解为什么一个一阶系统在阶跃响应输出下是一条单调上升的曲线了。这里用一张wikipedia里关于卷积的一张图形化解释，想要了解更多的同学可以自行跳转：Convolution

（特此感谢知乎学霸王尼莫的帮助）

卷积的应用

图像处理：用一个模板和一幅图像进行卷积，对于图像上的一个点，让模板的原点和该点重合，然后模板上的点和图像上对应的点相乘，然后各点的积相加，就得到该点的卷积值。对图像上的每个点都这样处理。由于多数模板都对称，所以模板不旋转。
卷积是一种积分运算，用来求两个曲线重叠区域面积。可以看作加权求和，可以用来消除噪声、特征增强。把一个点的像素值用它周围的点的像素值的加权平均代替。

卷积是一种线性运算,图像处理中常见的mask运算都是卷积，广泛应用于图像滤波。
卷积关系最重要的一种情况，就是在信号与线性系统或数字信号处理中的卷积定理。利用该定理，可以将时间域或空间域中的卷积运算等价为频率域的相乘运算，从而利用FFT等快速算法，实现有效的计算，节省运算代价。

下面是来自sselssbh博客的一个例子，非常形象的解释了卷积在图像领域的作用

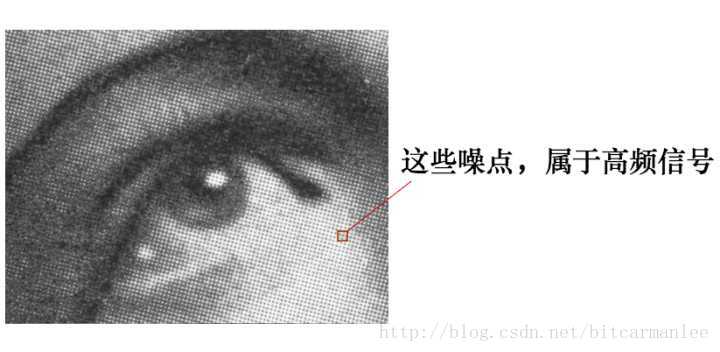
有这么一副图像，可以看到，图像上有很多噪点：
这里写图片描述

高频信号，就好像平地耸立的山峰：
这里写图片描述

看起来很显眼。

平滑这座山峰的办法之一就是，把山峰刨掉一些土，填到山峰周围去。用数学的话来说，就是把山峰周围的高度平均一下。

平滑后得到：
这里写图片描述

4.2 计算

卷积可以帮助实现这个平滑算法。

有噪点的原图，可以把它转为一个矩阵：
这里写图片描述

然后用下面这个平均矩阵（说明下，原图的处理实际上用的是正态分布矩阵，这里为了简单，就用了算术平均矩阵）来平滑图像：

记得刚才说过的算法，把高频信号与周围的数值平均一下就可以平滑山峰。

比如我要平滑点，就在矩阵中，取出点附近的点组成矩阵 f ,和 g 进行卷积计算后，再填回去
这里写图片描述

要注意一点，为了运用卷积， g 虽然和 f 同维度，但下标有点不一样：
这里写图片描述

这里写图片描述

写成卷积公式就是：

要求，一样可以套用上面的卷积公式。

这样相当于实现了 g 这个矩阵在原来图像上的划动（准确来说，下面这幅图把 g 矩阵旋转了）：

再比如做馒头

楼下早点铺子生意太好了，供不应求，就买了一台机器，不断的生产馒头。

假设馒头的生产速度是 f(t) ，那么一天后生产出来的馒头总量为： ∫240f(t)dt

馒头生产出来之后，就会慢慢腐败，假设腐败函数为 g(t) ，比如，10个馒头，24小时会腐败： 10∗g(t)

想想就知道，第一个小时生产出来的馒头，一天后会经历24小时的腐败，第二个小时生产出来的馒头，一天后会经历23小时的腐败。如此，我们可以知道，一天后，馒头总共腐败了： ∫240f(t)g(24−t)dt

文章也发表在我的个人博客中：点击打开链接，更多与机器学习，数学相关知乎，欢迎访问~

参考文章：

1. CSDN：最容易理解的对卷积(convolution)的解释http://blog.csdn.net/bitcarmanlee/article/details/54729807

2. 知乎：如何通俗易懂的解释卷积？https://www.zhihu.com/question/22298352

3. 卷积为什么叫卷子？https://www.zhihu.com/question/54677157

4. 果壳：关于卷积的一个血腥讲解 https://www.guokr.com/post/342476/

5. 小木虫：https://zh.wikipedia.org/wiki/%E5%8D%B7%E7%A7%AF%E5%AE%9A%E7%90%86