一、典型示例
考虑如下所示的4×4网格。

图1
非终端状态为S = {1, 2, . . . , 14}。在每个状态下有四种可能的行为,A = {up, down, right, left},这些行为除了会将代理从网格上移走外,其他都会确定性地引起相应的状态转换。因此,例如,p(6|5, right) = 1,p(10|5, right) = 0,p(7|7, right) = 1。这是一个无折扣的、分段的(episodic)任务。在到达终端状态之前的所有转换中,奖励为s1。终端状态在图中被着色(尽管它显示在两个地方,但它在形式上是一个状态)。预期奖励函数r(s, a, s0) = =1 对于所有状态s、s0和行为a。假设代理遵循等概率随机策略(所有行为的可能性相等)。图2的左侧显示了通过迭代政策评估计算出的值函数{vk}的序列。最终估计值实际上是vπ,在这种情况下,对于每个状态,它给出了从该状态终止的预期步数的否定。

图2
小型网格世界中迭代策略评估的收敛。左侧一列是随机策略(所有动作均等)的状态值函数近似序列。右侧一列是与值函数估计相对应的贪婪策略序列(箭头的表示是所有实现最大值的动作)。最后一项策略只保证比随机策略有所改进,但在这种情况下,它和第三次迭代后的所有策略都是最优的。
二、策略改进
我们计算一个策略的价值函数的理由是为了找出更好的策略。假设我们已经确定了一个任意确定性策略π的价值函数vπ。对于一些状态s,我们想知道是否应该改变策略以确定性地选择一个动作a = π(s)。我们知道从s开始遵循当前政策有多好,即vπ(s),但是改变到新政策会更好还是更差呢?回答这个问题的其中一种方式是考虑在s中选择a并随后遵循现有政策π。这种行为的值是

关键标准在于这个值是否大于或小于vπ(s)。如果它更大,也就是说,如果在s中选择一次a然后遵循π比一直遵循π更好,那么人们就会期望每次遇到s时选择a会更好,并且新政策实际上会更好。 这是一个一般结果的特殊情况,该一般结果称为策略改进定理。让π和π0是任何一对确定性策略,对于所有的s∈S,

那么策略π0必须和π一样好或者更好。也就是说,它必须从所有状态s∈S获得更大或相等的期望回报:

此外,如果在任何状态下上式存在严格不等式,则至少在某个状态下存在严格不等式。这一结果特别适用于我们在前一段中考虑的两个策略,一个是原始的确定性策略π,另一个是除了π0(s) = a = π(s)之外与π相同的改变策略π0。显然,在除s以外的所有状态下都成立。因此,如果qπ(s, a) > vπ(s),则改变策略确实优于π。
证明策略改进定理的想法很容易理解。我们不断扩展qπ的一侧,并重新应用(4.7),直到得到vπ0(s)

到目前为止,我们已经看到,给定一个策略及其价值函数,我们可以很容易地评估在单个状态下对特定行动的政策变化。考虑在所有状态和所有可能的行为上的变化是很自然的延伸,在每个状态下选择根据qπ(s, a)看起来最好的行动。换句话说,考虑新的贪婪策略π0,由下式给出。
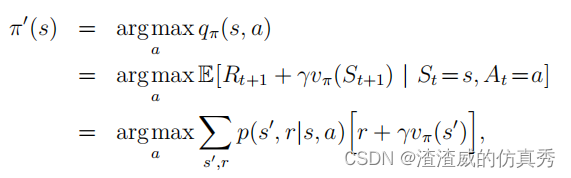
其中argmaxa表示后续表达式最大化的a值(任意打破平局)。贪婪策略采取的是短期内看起来最好的行动-在一步预测之后-根据vπ。通过构造,贪婪策略符合策略改进的条件,因此我们知道它与原始策略一样好,或者更好。通过使新政策对原始策略变得贪婪,从而改善原始策略的过程,称为策略改进。